Luz cuasiclásica: estados coherentes (Glauber) de radiación

Fuentes: esta entrada se basa principalmente en:

Cap. 3, Introductory Quantum Optics, de Gerry y Knight ([GER-05]).
Cap. 5, Quantum Optics, de Garrison y Chiao ([GAR-08]).
Cap. 5, Quantum Optics. An introduction, de M. Fox ([FOX-04]).
Roy J. Glauber: The quantum Theory of Optical Coherence, Physical Review 130-6 (1963) 2529.
Roy J. Glauber, Quantum Theory of Optical Coherence: Selected Papers and Lectures, Wiley VCH, ISBN-13 ‏ 978-352740687.

Glauber y el proyecto Manhattan

Documental: Roy J. Glauber era, hasta su fallecimiento con 93 años en 2018, el último superviviente del grupo de científicos del Proyecto Manhattan que desarrolló la bomba atómica en EEUU en 1945, al que se incorporó con tan sólo 18 años, colaborando en el estudio de la difusión de neutrones en reacciones en cadena. En el documental «That’s the story», el Prof. Glauber relata la vida en el laboratorio de Los Alamos y el proyecto de construcción de la bomba atómica.
Este gran científico fue galardonado en 2005, junto con John L. Hall y Theodor W. Hänsch, con el Premio Nobel de Física, por su contribución a la teoría cuántica de la coherencia óptica

Límite clásico de la radiación: estados coherentes o Glauber

La coherencia de la luz describe su «estabilidad»:
-Sólo las ondas coherentes pueden mostrar un patrón estable de interferencia.
-Ondas coherentes, en teoría ondulatoria clásica, pueden definirse en general como aquéllas que tienen una diferencia finita y estable entre sus frecuencias y fases: Coherencia
-«Coherencia» alude a la relación de dependencia estadística entre sendos vectores intensidad de campo eléctrico en dos puntos del espacio-tiempo. «Mayor coherencia» implicará, en primera aproximación, una interferencia con mayor visibilidad, o una polarización mejor definida, lo que conllevará, en general, el poder realizar mejores observaciones y medidas.

Introducida la cuantización del campo electromagnético, los denominados estados coherentes o cuasi-clásicos, estados Glauber (1963), se consideran los estados de radiación más clásicos (límite clásico), y se identifican con los autoestados del operador destrucción $\hat{a}$ , en los que las fluctuaciones del campo electromagnético son mínimas.

Un estado coherente es un estado cuántico de oscilador armónico de un conjunto particular específico caracterizado porque la dinámica de sus elementos presenta la mayor similitud posible con la correspondiente a las funciones del oscilador clásico. Estudiados por Schrödinger en 1926, a partir de la búsqueda de funciones del oscilador cuántico que satisfacieran el principio de correspondencia de Bohr, los estableció como los estados del oscilador cuántico caracterizados por ser paquetes gaussianos de mínima indeterminación, esto es, que alcanzan la igualdad en la correspondiente relación de indeterminación posición-momento.

Referencias fundamentales:
R.J. Glauber, “Photon Correlations», Physical Review Letters 10(3) (1963) 84.
E.C.G. Sudarshan; “Equivalence of semiclassical and quantum mechanical descriptions of statistical light beams”, Physical Review Letters 10(7) (1963) 277; C.L. Mehta and E.C. Sudarshan, “Relation between quantum and semiclassical description of optical coherence”, Physical Review 138(1B) (1965) B274.

J. O. Cortés-Tamayo: Estados coherentes del campo de radiación, Revista Mexicana de Física 38, No. 2 (1992) 309-331:

Los estados coherentes fueron descubiertos por E. Schrödinger en 1926 en el oscilador armónico simple. Él encontró funciones de onda que siguen el movimiento clásico de una partícula y cuyos perfiles son temporalmente estacionarios. Sin embargo, fueron introducidos en la óptica cuántica por Glauber en 1963 mediante el estudio de la coherencia de los campos de radiación cuantizados; fue en ese contexto que se les denominó estados coherentes.
Por un lado, el concepto de coherencia usado convencionalmente en óptica clásica implica que dos valores del campo de un haz de luz en puntos espacio-tiempo muy separados se encuentran correlacionados y que cuando se usan medios ópticos para superponerlos resultan franjas de intensidad; el ejemplo típico es el experimento de interferencia de Young. No obstante, este concepto requiere de un solo detector, el cual mide la intensidad o en otras palabras el cuadrado de la amplitud del campo y está confinado a describir haces monocromáticos y estacionarios en el tiempo. Con esto es posible caracterizar todos los experimentos típicos de la óptica clásica, como son los experimentos de difracción e interferencia. Esta coherencia clásica se introduce a través de la función de visibilidad de las franjas de interferencia en el experimento de Young, y se formula mediante la teoría estadística de cuasiprobabilidad.
Como la coherencia de un haz de luz está relacionada con las correlaciones que éste experimenta en intervalos considerables de distancia y tiempo, la idea de R.J. Glauber en 1963 fue examinar un experimento más general en que se colocan $n$ detectores en diferentes puntos espacio-tiempo para registrar correlaciones de $n$ fotones. Buscando que la teoría fuese consistente en el límite clásico de gran número de fotones, Glauber estudió el problema de radiación y fotoestadística mediante la discusión de sus propiedades de correlación y coherencia. De dicho estudio encontró en forma natural el concepto de estado coherente, el cual resultó único en la descripción de los haces de luz que ocurren en óptica coherente y que cuánticamente corresponden a estados en que el número de fotones es grande e intrínsecamente incierto, lo que no ofrecían otras representaciones de la luz como la formulada mediante los estados de Fock, cuyo número de fotones está bien determinado pero que describen insatisfactoriamente tales problemas. Por ejemplo, las densidades de probabilidad en la localización de los fotones, muestran diferencias apreciables con los perfiles clásicos correspondientes, pero aunque esta diferencia disminuye conforme el número de fotones crece, también crece el nivel de ruido del sistema.
De esa manera, los estados coherentes de Glauber satisfacen el principio de correspondencia de Bohr, es decir, los campos cuánticos coherentes reproducen a las ondas electromagnéticas clásicas con gran precisión en el límite de muchos fotones; son la contraparte cuántica más próxima a un campo clásico en el límite clásico. Además mantienen al sistema con la mínima fluctuación permitida por el principio de incertidumbre de Heisenberg, correspondiente a la fluctuación del vacío, justificando que también se les llame estados de mínima incertidumbre.

S. Cruz y Ó. Rosas-Ortiz: Estados coherentes y gatos de Schrödinger:
Por otro lado, en 1927, Paul Adrien Maurice Dirac combinó la formulación Maxwelliana de la luz con el concepto de un oscilador cuántico y obtuvo una descripción cuántica de la radiación electromagnética. En general, las predicciones de la formulación de Dirac no empatan del todo con los resultados de Maxwell ya que corresponden a dos descripciones diferentes de un mismo sistema, aplicables cada una de ellas en extremos opuestos del comportamiento de la luz.
En 1963 John R Glauber propone un modelo cuántico de la luz que permite hacer predicciones muy similares a las de Maxwell al tiempo que preserva la estructura teórica establecida por Dirac. De acuerdo con Glauber, la luz de Dirac debe producirse en estados de polarización coherentes si ésta ha de compararse con la luz Maxwelliana. […]Los estados coherentes de Glauber llamaron de inmediato la atención de la comunidad científica y fomentaron un sinfín de desarrollos teóricos y experimentales.
Los estados coherentes de John R. Glauber entrelazan los resultados de Maxwell y los de Dirac y permiten dar una descripción cuántica del comportamiento clásico de la luz. […]Para compaginar las predicciones de la teoría cuántica con las predicciones de la formulación Maxwelliana lo mejor que podemos hacer es usar los estados coherentes del oscilador cuántico. En este sentido, la radiación electromagnética que pueda describirse en términos de los vectores no sólo es altamente coherente sino que también es la que más se asemeja, en su comportamiento, al concepto Maxwelliano de la luz. Entonces, la combinación de las formulaciones de Maxwell, Dirac y Glauber permite dar una descripción completamente satisfactoria de los comportamientos clásico (interferencia) y cuántico (efecto fotoeléctrico) de la luz así como de la transición entre ellos (estados coherentes).

Estados coherentes en el blog «La-mecanica-cuantica.blogspot.com«, de Armando Martínez Tellez:

La superposición de estados del oscilador armónico simple para producir un estado coherente, llamémosla función de onda Glauber, está determinada por el requerimiento de que los coeficientes usados para producir la combinación linear de funciones de onda conducentes a un estado coherente Glauber tengan una distribución normal (Gaussiana).

Esto es en esencia lo que nos muestra el simulador de estados coherentes de la Universidad de Bergen para el estado n=4. Hay desde luego un estado coherente que corresponde al número cuántico n=2, y otro estado coherente que corresponde al número cuántico n=25, y así por el estilo. Lo verdaderamente importante es que la mezcla de estados se tiene que llevar a cabo con los coeficientes usados en la combinación linear de funciones de base obedeciendo rigurosamente una distribución Gaussiana:

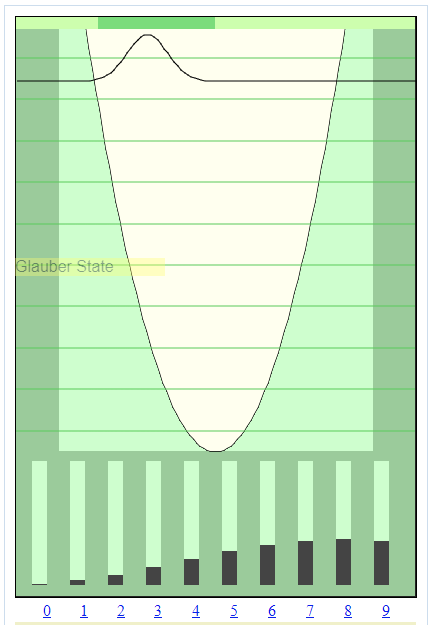
estado coherente de Glauber — Estado coherente de Glauber obtenido superponiendo diversos estados del oscilador con los coeficientes apropiados (imagen tomada del blog lamecanicacuantica.blogspot.com, procedente a su vez de un simulador de la Universidad de Bergen).

Puesto que las amplitudes relativas de las funciones de onda que son mezcladas tienen que seguir estrictamente un patrón Gaussiano, parecería que producir estados coherentes en el laboratorio debería ser una cosa endiabladamente difícil. Sin embargo, no es así, porque la misma Naturaleza se encarga de optimizar las cosas, sobre todo tomando en cuenta que la distribución Gaussiana es precisamente la que minimiza el producto de incertidumbres (algo parecido a lo que ocurre con el principio de mínima acción con el cual la Naturaleza misma encarga de buscar la ruta mínima cuando hay varias rutas menos eficientes posibles). Ésto facilita las cosas, ya que de no ser así el hombre no habría podido producir el rayo láser.

Los estados coherentes no fueron descubiertos por Roy Glauber. Hay que ir atrás a los tiempos de Erwin Schrödinger, precisamente el descubridor de la ecuación de onda cuántica, quien fue el que los encontró por vez primera en 1926 como el primer ejemplo de lo que se considera la dinámica cuántica basada en la ecuación de onda dependiente del tiempo. Schrödinger obtuvo sus estados coherentes como paquetes de onda Gaussianos de “incertidumbre mínima” (mínima en el sentido de que se pudiera minimizar el producto de las incertidumbres en la posición q y el momentum p que de acuerdo a lo que descubrió Werner Heisenberg puede ser igual o mayor a ħ/2 pero no puede ser menor que ħ/2) mientras buscaba soluciones a su ecuación de onda que satisfacieran el principio de correspondencia que afirma que los resultados obtenidos en la Mecánica Cuántica se deben ir aproximando más y más a las mismas ecuaciones y fórmulas de la mecánica clásica conforme van aumentando los números cuánticos n que describen al sistema submicroscópico, o sea conforme n tiende al infinito, o lo que es lo mismo, conforme el valor de la constante de Planck ħ es cambiado y se le hace tender a cero. En pocas palabras, Schrödinger estaba interesado en lograr sistemas cuánticos que para números cuánticos grandes reprodujeran los resultados ya conocidos en la mecánica clásica. Para los fundadores de la Mecánica Cuántica, era obvio que la Mecánica Cuántica no era un “caso especial” de la mecánica clásica, simple y sencillamente no había manera alguna de poder derivar la Mecánica Cuántica de la mecánica clásica, atribuíble filosóficamente al hecho de que ultimadamente todos los cuerpos macroscópicos están constituídos por átomos y moléculas, y en todo caso debería ser la mecánica clásica la que se pudiese derivar de la Mecánica Cuántica “para números cuánticos grandes”. Pero… ¿era posible lograr tal conexión teórica entre la teoría que rije los fenómenos del mundo submicroscópico, una teoría de índole esencialmente probabilista, con la mecánica Newtoniana que rije los fenónemos del mundo macroscópico, de índole cien por ciento determinista? En sus esfuerzos por lograr tal objetivo, Schrödinger daba por hecho que era necesario trabajar sobre sistemas y cosas que minimizaran la inevitable incertidumbre que trae consigo el principio de incertidumbre de Heisenberg. Y los estados coherentes para el oscilador armónico simple le parecieron a Schrödinger un punto ideal de partida, aunque no llegó más lejos dadas las limitaciones teóricas y tecnológicas de su época. De cualquier modo, desde aquél entonces el estado coherente fue establecido como un estado de incertidumbre mínima, con el único parámetro libre escogido para hacer la dispersión natural (la desviación estándard estadística σ en unidades naturales adimensionales) igual para la posición y el momentum, cada uno siendo igualmente pequeño a energías relativamente altas. Como vimos arriba en el ejemplo proporcionado por el simulador, en contraste con los eigenestados estáticos de energía del sistema, la evolución temporal de un sistema coherente está concentrada a lo largo de trayectorias clásicas. La dinámica del estado coherente del oscilador armónico cuántico linear surge inesperadamente en una amplia variedad de sistemas físicos, ocurriendo sobre todo en la teoría cuántica de la luz fundamentada en la electrodinámica cuántica.

Poco tiempo después de los esfuerzos de Schrödinger, la ruta teórica hacia el entendimiento de la coherencia de estados empezó en cierto modo cuando en 1927 Paul Adrien Maurice Dirac combinó la formulación Maxwelliana de la luz en su aspecto ondulatorio con el concepto del oscilador armónico cuántico obteniendo de éste modo una descripción cuántica de la radiación electromagnética mediante la cuantización del campo electromagnético. En general, las predicciones de la formulación de Dirac no empatan del todo con los resultados de Maxwell ya que corresponden a dos descripciones diferentes de un mismo sistema, aplicables cada una de ellas en extremos opuestos del comportamiento de la luz. Fue en 1963 cuando Roy Glauber en su trabajo “The Quantum Theory of Optical Coherence” publicado en el Physical Review Letters propuso un modelo cuántico de la luz que permite hacer predicciones muy similares a las de Maxwell al tiempo que preserva la estructura teórica establecida por Dirac. De acuerdo con Glauber, la luz de Dirac debe producirse en estados de polarización coherentes si ésta ha de compararse con la luz Maxwelliana. Los estados coherentes de Glauber llamaron de inmediato la atención de la comunidad científica y fomentaron un sinfín de desarrollos teóricos y experimentales. Tomando en cuenta lo anterior, cabe preguntarse hasta dónde es posible dar una descripción cuántica de los sistemas macroscópicos. En 1935 Schrödinger dió a conocer su diseño de su famoso experimento Gedanken donde se involucran un inocente gato y la desintegración de un átomo (decaimiento atómico). Para mostrar las “aparentes contradicciones” de la teoría cuántica con el “concepto de realidad” Schrödinger primero le adjudica un estado cuántico al gato, después mezcla éste último con el estado cuántico del átomo para concluir que el gato estará vivo y muerto a la vez en tanto no lo “observemos”. Sorprendentemente, se pueden usar los estados coherentes de Glauber para representar al sistema cuántico del gato, incluso a nivel experimental.

El mérito de Roy Glauber, ganador del Premio Nóbel de Física en 2005, fue haber rescatado el tema de los estados coherentes del olvido dándoles el impulso teórico necesario para fundamentar sobre bases sólidas el campo científico hoy conocido como la óptica cuántica. En la óptica cuántica, el estado coherente se refiere a un estado del campo electromagnético cuantizado que describe una máxima especie de coherencia y una especie de comportamiento clásico. Hoy, estos estados del oscilador armónico, estados coherentes conocidos como estados Glauber, son considerados prototipos del campo electromagnético oscilante, siendo el modelo del campo de onda continuo del láser, o del campo electromagnético de una onda de radio no modulada.

Estados coherentes: Autoestados del operador destrucción

Sea $|\alpha>$ un autoestado del operador $\hat{a}$ (que no es hermítico),

$\hat{a}|\alpha>=\alpha|\alpha>\, \alpha \in \mathbb{C}$

$<\alpha|\hat{a}^+=<\alpha|\alpha^*$

-Expresado en la base del espacio de Fock:

$|\alpha>=\sum_n c_n|n>$

$\Rightarrow \hat{a}|\alpha>=\alpha |\alpha>=$ $\alpha \sum_n c_n|n>=\sum_n c_n\hat{a}|n>=$ $\sum_n c_n\sqrt{n}|n-1>$

$\Rightarrow \alpha c_0=0\;;\;\alpha c_{n-1}=c_n\sqrt{n}\; \forall n\ge 1$

$\Rightarrow c_n=\frac{\alpha^n}{\sqrt{n!}}\; \forall n\ge 1$

$\Rightarrow |\alpha>=c_0\sum_n \frac{\alpha^n}{\sqrt{n!}}|n>$

que normalizando resulta

$|\alpha>=e^{-\frac{1}{2}|\alpha|^2}\sum_n \frac{\alpha^n}{\sqrt{n!}}|n>$

Propiedades de los estados coherentes:

Valor medio del campo eléctrico (para un modo $\omega$ ):
$<\alpha|\hat{E}_x(\vec{r},t)|\alpha>=<\alpha|i(\frac{\hbar\omega}{2\epsilon_0V})^{\frac{1}{2}}[\hat{a}e^{i(\vec{k}\cdot\vec{r}-\omega t)}-\hat{a}^+e^{-i(\vec{k}\cdot\vec{r}-\omega t)}]|\alpha>$
$=i(\frac{\hbar\omega}{2\epsilon_0V})^{\frac{1}{2}}[\alpha e^{i(\vec{k}\cdot\vec{r}-\omega t)}-\alpha^*e^{-i(\vec{k}\cdot\vec{r}-\omega t)}]$ -Introduciendo $\alpha=|\alpha|e^{i\theta}$ : $<\alpha|\hat{E}_x(\vec{r},t)|\alpha>=2|\alpha|(\frac{\hbar\omega}{2\epsilon_0V})^{\frac{1}{2}}\sin (\omega t -\vec{k}\cdot\vec{r} -\theta)$ $<\alpha|\hat{E}_x^2(\vec{r},t)|\alpha>=\frac{\hbar\omega}{2\epsilon_0V}[1+4|\alpha|^2\sin^2 (\omega t -\vec{k}\cdot\vec{r} -\theta)]$
que tiene la forma clásica.
Fluctuaciones del campo eléctrico: $\Delta_{\alpha}\hat{E}_x=(\frac{\hbar\omega}{2\epsilon_0V})^{\frac{1}{2}}$
-Las fluctuaciones son las que corresponden al vacío: los estados coherentes contienen sólo el ruido del vacío.
Fluctuaciones de las cuadraturas de campo:
$\Delta_{\alpha} \hat{X}_1=\Delta_{\alpha} \hat{X}_2=\frac{1}{2}$

–Los estados coherentes tienen las fluctuaciones del vacío de Fock, y los operadores cuadratura saturan sobre ellos la desigualdad del principio de indeterminación.
Valor medio del operador número, su cuadrado y su indeterminación:
$\overline{n}=<\alpha|\hat{n}|\alpha>=|\alpha|^2$
$<\alpha|\hat{n}^2|\alpha >=$ $|\alpha |^4+|\alpha |^2= \overline{n}^2+\overline{n}$
$\Delta_{\alpha} \hat{n}=\sqrt{<\hat{n}^2>-<\hat{n}>^2}=\overline{n}^{\frac{1}{2}}$ ,
donde la última expresión es característica de la distribución estadística de Poisson.
La variancia conjunta de los operadores creación y destrucción, $V_{\alpha}(\hat{a},\hat{a}^+)$ , es nula sobre un estado de Glauber:
$V_{\alpha}(\hat{a},\hat{a}^+)=\left\langle (\hat{a} -\left\langle \hat{a} \right\rangle) (\hat{a}^+ -\left\langle \hat{a}^+ \right\rangle)\right\rangle$
$=\left\langle \hat{a}\hat{a}^+ \right\rangle - \left\langle \hat{a} \right\rangle \left\langle \hat{a}^+ \right\rangle$
$=\left\langle \hat{a}\hat{a}^+\right\rangle -\left\langle \hat{a}\right\rangle \left\langle \hat{a}^+\right\rangle =0$

-Por tanto, los operadores escalera resultan estadísticamente independientes sobre un estado cuasi-clásico. Esta es una propiedad fundamental y definitoria para el límite clásico de la radiación.
Expresión en representación de coordenadas:
$\hat{q}|q>=q|q>\;;\;\Psi_{\alpha}(q)=<q|\alpha>$
$\rightarrow \hat{q}\Psi_{\alpha}(q)(q)=q\Psi_{\alpha}(q)$
$\rightarrow \hat{p}\Psi_{\alpha}(q)(q)=-i\hbar\frac{d}{dq}\Psi_{\alpha}(q)$
$\rightarrow \Psi_{\alpha}(q)=(\frac{\omega}{\hbar \pi})^{\frac{1}{4}}e^{-|\alpha^2|/2}\sum_n \frac{(\alpha / \sqrt{2})^n}{n!} H_n(\xi)$ $=(\frac{\omega}{\hbar \pi})^{\frac{1}{4}}e^{-|\alpha^2|/2} e^{\xi^2/2}e^{-(\xi - \alpha /\sqrt{2})^2}$ ,
una gaussiana en la que $\xi=q\sqrt{\frac{\omega}{\hbar}}$ y $H_n$ representa el polinomio de Hermite de grado $n$ .
-La densidad de probabilidad $|\Psi_{\alpha}(q)|^2$ es una gaussiana centrada en $q=q_0$ .
-Expresión en representación de momentos (transformada de Fourier):
$\Phi_{\alpha}(p)=<p|\alpha>={\pi\hbar \omega}^{-\frac{1}{4}}e^{-\frac{(p-p_0)^2}{4\Delta p_0^2}}e^{iq_0p/\hbar}$ ,
donde $\Delta p_0=\sqrt{\frac{\hbar\omega}{2}}$
Su evolución temporal viene dada por:
$|\alpha , t> = e^{-i \hat{H}t/\hbar}| \alpha> =e^{-i\omega t/2}e^{-i\omega t \hat{n}}| \alpha>=e^{-i\omega t/2} |\alpha e^{-i\omega t}>$ ,
$\rightarrow \Psi_{\alpha}(q,t)=(\frac{\omega}{\hbar \pi})^{\frac{1}{4}}e^{-|\alpha^2|/2} e^{\xi^2/2}e^{-(\xi - \alpha e^{-i\omega t}/\sqrt{2})^2}$ ,
de modo que el estado coherente permanece como tal estado coherente bajo evolución temporal libre, manteniendo la forma de una gaussiana cuyo centro se comporta como el del paquete asociado a una partícula material sometida a un potencial de oscilador armónico. En resumen: en contraste con los autoestados de energía del sistema, la evolución temporal de un estado coherente sigue las trayectorias clásicas:
Dinámica casi-clásica de un estado coherente (Fuente: Wikipedia).

-Esta conducta es análoga para todos los estados coherentes: la radiación electromagnética descrita por los estados coherentes es la que más se asemeja a la descripción Maxwelliana.
Principio de indeterminación: entre los estados del oscilador armónico, el único «simple» (con expresión $|n>$ ) que satura la desigualdad del principio de indeterminación, esto es, alcanza la igualdad, es el vacío, n=0, un estado de «incertidumbre mínima», o estado MUS. Y de hecho, para todos los demás estados el producto de indeterminaciones en posición y momento irá aumentando conforme lo haga el número cuántico n del autoestado $|n>$ , como ya estudió Schrödinger. Pero existen ciertas combinaciones lineales, los estados coherentes o estados Glauber, que también minimizan el producto de las sendas indeterminaciones de los operadores posición y momento. Y resulta que, matemáticamente, son las autofunciones del operador destrucción o descenso $\hat{a}$ :
$\Delta_{\alpha} q \Delta_{\alpha} p =\frac{\hbar}{2}$

Los estados coherentes son estados de mínimo producto de indeterminaciones (MUS, minimum uncertainty states, como el vacío de Fock), con iguales valores de las sendas indeterminaciones en posición y momento.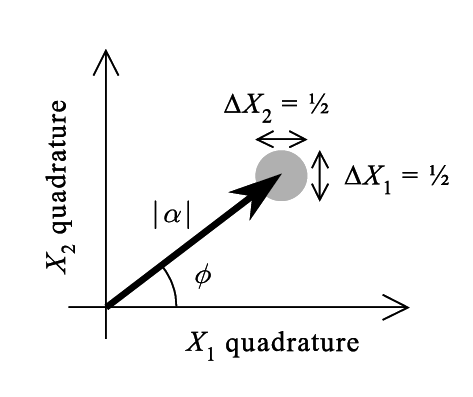

Diagrama de fase de un estado coherente; el círculo sombreado representa la indeterminación cuántica.

-Los estados coherentes pueden por ello ser considerados como «estados del vacío desplazados», con el círculo de indeterminación del vacío desplazado respecto al origen por el vector $\alpha$ .
Operador unitario desplazamiento:
-el operador $\hat{d}(\alpha)=e^{\alpha \hat{a}^{\dagger}-\alpha^* \hat{a}}$ es un operador unitario ( $\hat{d}^{\dagger}\hat{d}=\hat{d}\hat{d}^{\dagger}=\hat{I}$ ) que genera sobre el vacío los estados coherentes:
$\hat{d}(\alpha)|0>=|\alpha>$
-Propiedades:
$\hat{d}(\alpha)=e^{-\frac{1}{2}|\alpha|^2}e^{\alpha \hat{a}^{\dagger}}e^{-\alpha^* \hat{a}}$
$=e^{\frac{1}{2}|\alpha|^2}e^{-\alpha^* \hat{a}}e^{+\alpha \hat{a}^{\dagger}}$
$\hat{d}^{\dagger}(\alpha)=\hat{d}(-\alpha) =e^{-\frac{1}{2}|\alpha|^2}e^{-\alpha \hat{a}^{\dagger}}e^{\alpha^* \hat{a}}$
$|\alpha>=\hat{d}(\alpha)|0>=e^{-\frac{1}{2}|\alpha|^2}\sum_{n=0}^{\infty}\frac{\alpha^n}{\sqrt{n!}}|n>$ $\hat{d}^{-1}(\alpha) \hat{a} \hat{d}(\alpha)=\hat{a}+\alpha$ $\hat{d}^{-1}(\alpha) \hat{a}^{\dagger} \hat{d}(\alpha)=\hat{a}^{\dagger}+\alpha^*$ $\hat{d}(\alpha)\hat{d}(\beta)|0>= \hat{d}(\alpha)|\beta>=e^{iIm(\alpha \beta^*)}|\alpha + \beta>$ .
Nota: recuérdese:
$e^{\hat{A}+\hat{B}}=e^{\hat{A}}e^{\hat{B}}e^{-\frac{1}{2}[\hat{A},\hat{B}]}$ ,
$[\hat{A},\hat{B}]\ne 0$
y $[\hat{A}, [\hat{A},\hat{B}]]=[\hat{B}, [\hat{A},\hat{B}]]=0$ .
Probabilidad de que el resultado de la medida del número de fotones en el campo, sobre un estado coherente, sea $n$ :
$P(n)=| <n | \alpha> |^2 = \frac{(\overline{n})^n}{n!} e^{-\overline{n}} \$
-Esta probabilidad es la correspondiente a una distribución de Poisson:
Probabilidad de detección de n fotones, o distribución estadística fotónica, en un estado coherente: se trata de una distribución de Poisson, por tanto, la varianza coincide con el número medio de fotones (puntos para valores experimentales y barras para los teóricos) (fuente: Wikipedia).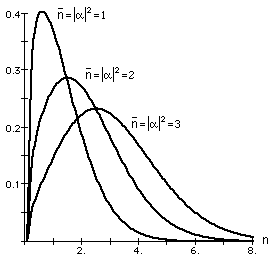

COHERENT STATE PHOTON STATISTICS (http://people.seas.harvard.edu/~jones/ap216/lectures/ls_3/ls3_u3/ls3_unit_3.html).
Distribución de fase: para un estado coherente $|\alpha>$ , la correspondiente función de distribución de fase viene dada por:
$P(\varphi)=\frac{1}{2\pi} |<\varphi|\alpha>|^2=\frac{1}{2\pi}e^{-|\alpha|^2|\sum_ne^{in(\varphi - \theta)}\frac{|\alpha|^n}{\sqrt{n!}}|^2}$
-Para $|\alpha|$ grande, la distribución de Poisson puede aproximarse por la de Gauss, derivándose:
$P(\varphi)\approx (\frac{2|\alpha|^2}{\pi})^{\frac{1}{2}}e^{-2|\alpha|^2(\varphi-\theta)^2}$ ,
que no es sino una gaussiana con máximo en $\varphi=\theta$ , y cuya anchura va disminuyendo conforme $\overline{n}=|\alpha|^2$ aumenta: los estados coherentes devienen en bien localizados en fase al aumentar el número medio de fotones.
Los estados coherentes constituyen una base del espacio de Fock, ya que resuelven la identidad en el espacio de fases, pero son sólo estrictamente ortogonales cuando $|\alpha -\beta|$ es grande:
$<\beta|\alpha>=e^{-\frac{1}{2}|\alpha|^2-\frac{1}{2}|\beta|^2+\alpha \beta^*}$
-Nota: De hecho, el conjunto de todos los estados coherentes o estados Glauber como base es redundante, en el sentido de ser sobrecompleto («overcomplete»), esto es, sigue siendo completo si se quitan algunas funciones del conjunto (ya que no constituyen un conjunto linealmente independiente).

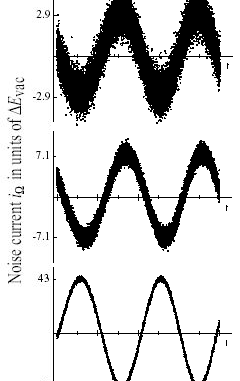
Pese a todas las características anteriores, un estado coherente presenta siempre características cuánticas: a la forma sinusoidal del campo se superponen las fluctuaciones cuánticas, con un efecto tanto mayor cuanto menor es $|\alpha|$ .

En las siguientes figuras, se representa el campo electromagnético asociado a un estado coherente:

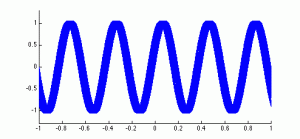
Imagen de R.V. Jones, Harvard lectures. — Imágenes de R.V. Jones, Harvard lectures ( $|\alpha|$ disminuyendo conforme aumenta el ruido).

-Conforme $|\alpha|$ aumenta, el campo tiende a un comportamiento más clásico.

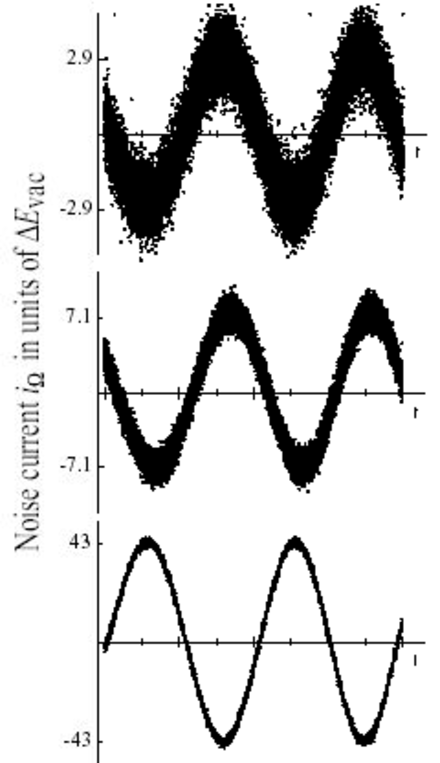
Ruido en estados coherentes: El campo eléctrico, medido por detección óptica homodina (una sola frecuencia), en función de la fase para tres estados coherentes emitidos por un láser Nd: YAG. La cantidad de ruido cuántico en el campo eléctrico es completamente independiente de la fase. A medida que aumenta la intensidad de campo, es decir, la amplitud de oscilación α del estado coherente, el ruido cuántico o la incertidumbre son constantes en 1/2 y, por lo tanto, se vuelven cada vez menos significativos. En el límite de un campo grande, el estado se convierte en una buena aproximación de una onda clásica estable sin ruido. Los números de fotones promedio de los tres estados de arriba a abajo son ⟨n⟩ = 4.2, 25.2, 924.5 (Fuente: Wikipedia, a partir de Nature, volume 387, 1997, pages471–475).

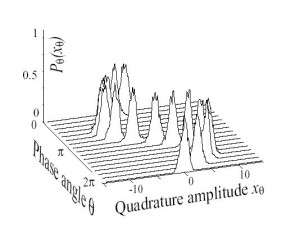
By Gerd Breitenbach (dissertation) CC-BY-SA-3.0, via Wikimedia Commons. — Figura de Gerd Breitenbach (dissertation) CC-BY-SA-3.0, via Wikimedia Commons: se representa el paquete de ondas oscilante correspondiente al segundo estado coherente (⟨n⟩ = 4.2, 25.2) en la anterior figura; la distribución se corresponde con una gaussiana que mantiene su anchura para todas las fases del campo.

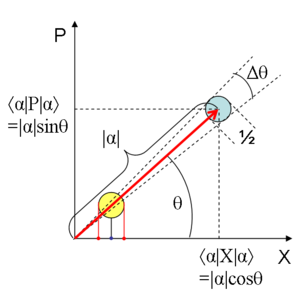
Diagrama de fases de un estado coherente, mostrando como la indeterminación en un estado coherente se distribuye por igual entre los sendos ejes correspondientes a las cuadraturas. El intervalo marcado en rojo sobre el eje de abscisas se corresponde con las fronteras del ruido en las figuras anteriores (Fuente: Wikipedia).

Los estados coherentes o de Glauber se conceptualizan como los estados cuánticos de luz más próximos a los estados clásicos de luz coherente.

-Podría decirse que un estado coherente es el análogo cuántico de una onda plana monocromática clásica.
-La luz láser se conceptualiza con frecuencia como luz emitida por una multitud de fuentes luminosas en fase, pero, estrictamente, la imagen de concordancia en fase entre fotones es inválida: el modelo cuántico correcto para un láser ideal es un estado coherente, la contrapartida cuántica de la onda electromagnética estable (la primera onda azul representada en la figura más arriba, $\alpha$ grande).

(Nota: sobre la controversia alrededor de las afirmaciones en el último párrafo, y sobre la adecuación de los estados Glauber como modelo teórico de la luz láser, puede consultarse [GAR-08], pp. 157ss).

Bibliografía

[FOX-04] Fox, M.; Quantum Optic. An introduction. Oxford Univ. Press; Oxford, 2004. ISBN: 0-19?856672-7, 978-0-19-856672-4.
[GAR-08] Garrison, J. C. and R. Y. Chiao, Quantum Optics, Oxford Univ. Press, Oxford, 2008. ISBN: 978-0-19-850886-1.
[GER-05] Gerry, C. C. and Knight, P. L., Introductory Quantum Optics, Cambridge Univ. Press, Cambridge, 2005. ISBN: 0-521-82035-9.

-Estados coherentes y su representación:
J. O. Cortés-Tamayo: Estados coherentes del campo de radiación.

Estados coherentes en el blog lamecanicacuantica.blogspot.com.

Estados coherentes en el proyecto Wolfram: https://demonstrations.wolfram.com/CoherentStatesOfTheHarmonicOscillator/

Simulación: https://physics.weber.edu/schroeder/software/HarmonicOscillator.html

Estados coherentes en la Wikipedia: https://en.wikipedia.org/wiki/Coherent_state

Rüdiger Paschotta, RP Photonics Encyclopedia.

Tesis doctoral de E. Martín Fierro, Univ. de La Laguna: «Los estados coherentes en la descripción semiclásica de la mecánica cuántica«.

Trabajo Fin de Grado de D. Benedicto, Univ. de Zaragoza: «Desarrollo de herramientas tomográficas y visuales en mecánica cuántica«.

Farit Ya. Khalili, Research Gate.

-Representaciones gráficas del campo cuántico en cavidades:
http://www.cqed.org/spip.php?article254.

S. Cruz y Ó. Rosas-Ortiz: Estados coherentes y gatos de Schrödinger.

-Representaciones en el espacio de fases: funciones $Q$ y de Wigner:
http://www.physics.miami.edu/~curtright/TimeDependentWignerFunctions.html