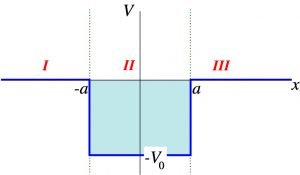
El pozo cuadrado finito
- Función potencial
:
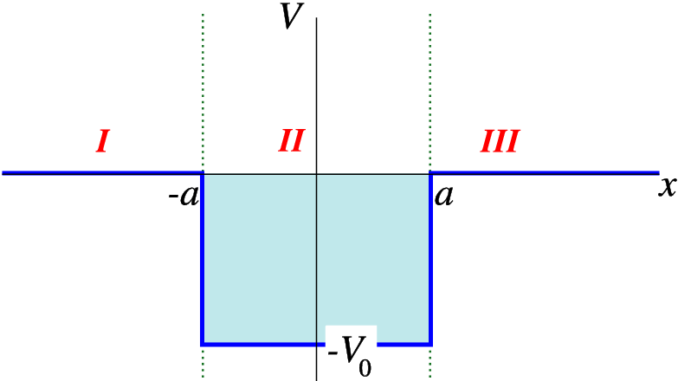
Imagen de oer.physics.manchester.ac.uk. - Problema de autovalores de energía:
,
y buscamos solucionesque sean funciones ella y su derivada primera
continuas
.
- Dependiendo de la región espacial considerada, la forma concreta de la EDO planteada es:
Zonas I y III :
Zona II : - La solución general de una EDO
,
donde,
, tiene la expresión:
-Signo (-) :
conescalares arbitrarios.
-Signo (+) :
conescalares arbitrarios.
- Se presentan pues los casos:
:
- Zonas I y III:
y
, respectivamente:
ambas con el mismo
yescalares arbitrarios.
- Zona II:
:
con
yescalares arbitrarios.
- Imponiendo las condiciones para que la solución sea físicamente aceptable:
-Acotación
-Acotación
-Continuidad deen
:
-Continuidad deen
:
-Continuidad deen
:
-Continuidad deen
:
-Puesto que este conjunto de condiciones conduce a la solución trivial, la conclusión es que no existen efectivamente soluciones físicamente aceptables del problema de autovalores de energía para valores del parámetro de separación.
- Zonas I y III:
:
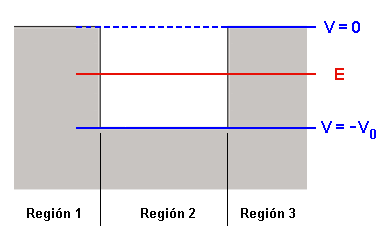
Imagen del blog http://la-mecanica-cuantica.blogspot.com.es/2010/07/transmision-y-reflexion-de-particulas_05.html. - Expresión de la función de onda en cada zona:
- Zonas I y III:
y
, respectivamente:
con un común
yescalares arbitrarios.
- Zona II:
:
; con
yescalares arbitrarios.
- Zonas I y III:
- Los estados ligados de un potencial monodimensional simétrico en torno al origen tienen paridad definida; incorporando el requisito de paridad definida se obtienen separadamente los dos tipos de soluciones:
- Soluciones de paridad par
:
- Han de satisfacer
y
, por lo que se tiene el conjunto de condiciones:
-Por ser una función par:
-Acotación para:
-Acotación para:
-Por ser una función par:
-Continuidad deen
:
-Continuidad deen
:
-Continuidad deen
:
-Continuidad deen
:
- La autofunción par tiene pues la expresión general:
donde
- Resolviendo:
(equivalentemente, puede escribirse la ecuación logarítmica
e incorporar la continuidad en).
-Se obtiene así una ecuación trascendente que debe resolverse para obtener las energías de los estados ligados pares.
- Han de satisfacer
- Soluciones de paridad impar
:
- Han de satisfacer
y
, por lo que se tiene el conjunto de condiciones:
-Por ser una función impar:
-Acotación para:
-Acotación para:
-Por ser una función impar:
-Continuidad deen
:
-Continuidad deen
:
-Continuidad deen
:
-Continuidad deen
:
- La autofunción impar tiene pues la expresión general:
donde
- Resolviendo:
(equivalentemente, puede escribirse la ecuación logarítmica
e incorporar la continuidad en, que conduce a la misma ecuación).
-Se obtiene así una ecuación trascendente que debe resolverse para obtener las energías de los estados ligados pares.
- Han de satisfacer
- Soluciones de paridad par
- Niveles de energía: las anteriores ecuaciones transcendentes requieren resolución bien numérica, bien gráfica. La solución gráfica es directa:
- Gráficamente, las soluciones pares corresponden a la intersección de las siguientes curvas
y
:
a)
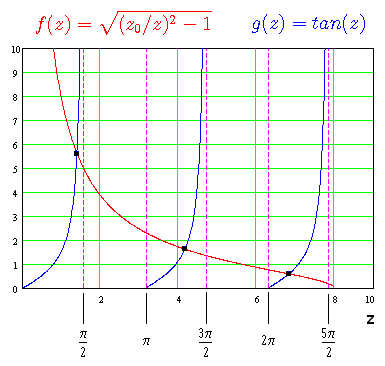
Figura (*): resolución autoestados pares; Imagen del blog la-mecanica-cuantica.blogspot.com. -La gráfica proporciona los valores de z en los cuales se cortan las dos funciones
y
. En el ejemplo representado, correspondiente a unos valores determinados de los parámetros del pozo
y
, hay tres de ellos (el número que haya dependerá del valor del parámetro
para cada pozo particular), luego el correspondiente pozo finito posee tres autoenergías o valores
para los cuales el problema posee solución par, esto es , una autofunción físicamente aceptable.
- Y las soluciones impares corresponden análogamente a la intersección de las siguientes curvas
y
:
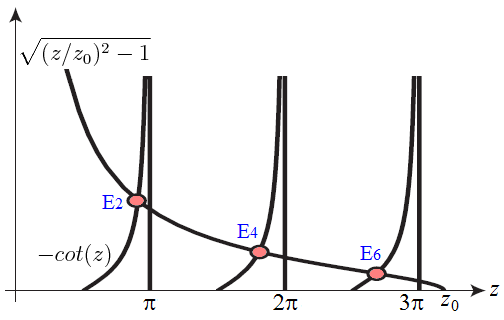
Imagen del blog la-mecanica-cuantica.blogspot.com. -La gráfica proporciona los valores de z en los cuales se cortan las dos funciones
y
: el correspondiente pozo finito posee tres autoenergías o valores
para los cuales el problema posee autofunción asociada impar.
- La siguiente gráfica reúne los autovalores correspondientes a las soluciones pares e impares, para dos valores distintos de la profundidad
del pozo (notación: aquí,
; en la figura,
):
- Otra posibilidad gráfica: dibujar las tres curvas que se indican en la siguiente figura:
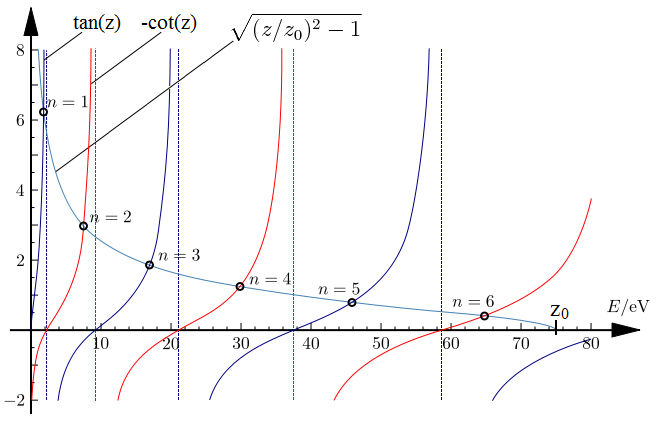
Gráfica en que se muestran tanto las soluciones pares (curvas de color azul) como las soluciones impares (curvas de color rojo) para un pozo de potencial que admite seis estados discretos de energía, para lo cual se ha supuesto una anchura del pozo L=2a igual a 0.4 nanómetros (a=0.2 nm) y una profundidad del pozo de potencial de 75 eV: (figura y su pie tomadas de: http://la-mecanica-cuantica.blogspot.com/2010/07/transmision-y-reflexion-de-particulas_05.html ; también disponible en: http://en.wikibooks.org/wiki/Materials_in_Electronics/Confined_Particles/1D_Finite_Wells). - Y otra alternativa más de resolución gráfica: optar por dibujar el círculo de radio
, puesto que se satisface
y localizar los puntos de corte con las curvas
y
:
,
respectivamente representadas en azul, púrpura y amarillo en la siguiente figura: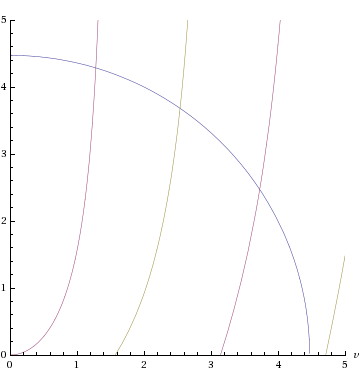
Imagen de la Wikipedia (http://en.wikipedia.org/wiki/Finite_potential_well).
- Gráficamente, las soluciones pares corresponden a la intersección de las siguientes curvas
- Análisis: Aparece el fenómeno de la cuantización de la energía, de modo que sólo para un conjunto de valores discretos de
existe solución físicamente aceptable al problema de autovalores.
-el número de estados ligados depende del caso concreto, es decir, de los valores particulares del conjuntomanejado, a través del parámetro
.
-Las autofunciones ligadas son estados no degenerados que satisfacen el teorema de oscilación: una vez ordenados en orden creciente de energía, los estados ligados de un potencial monodimensional simétrico van alternándose en paridad, siendo la autofunción del estado fundamental par (ya que una función par tiene siempre o ninguno o un número par de nodos, mientras que una función impar posee un número impar de ceros); la n-ésima función tiene (n-1) nodos (donde).
-De la observación de las gráficas correspondientes a las soluciones pares, se deduce que, para pozos tales que el parámetrosea muy grande (esto es, pozos muy profundos y no muy estrechos, por ejemplo), entonces las intersecciones van acercándose (siempre por debajo) a los valores
, que conducen a autovalores
, es decir, los autovalores del pozo cuadrado infinito (en la figura (*), «levantar» la curva roja).
-Cuandoes muy pequeño, va disminuyendo el número de estados ligados, pero al menos el primer estado par está siempre presente (en la figura (*), «agachar» la curva roja).
- Autofunciones de los estados ligados: Las primeras autofunciones ligadas se presentan en las siguientes figuras; obsérvese que penetran en la zona exterior del pozo, regiones I y III, en las que presentan un comportamiento exponencial, según
, de forma que penetran tanto más cuanto mayor sea el valor de la energía de ligadura o autovalor
.
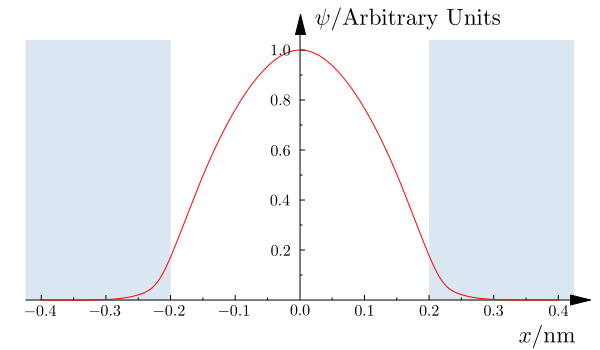
Imagen de http://en.wikibooks.org/wiki/Materials_in_Electronics/Confined_Particles/1D_Finite_Wells. 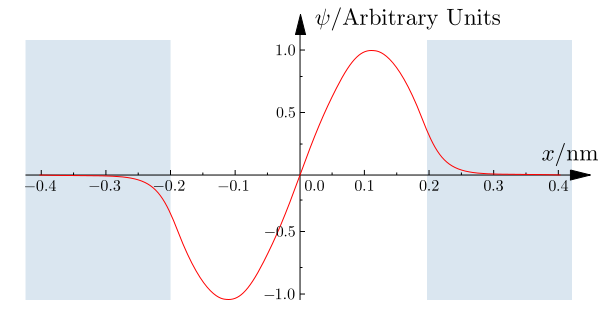
Imagen de http://en.wikibooks.org/wiki/Materials_in_Electronics/Confined_Particles/1D_Finite_Wells. - Las siguientes figuras ilustran las diferencias entre los autoestados ligados del pozo finito frente al pozo infinito:
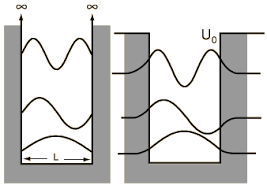
Imagen de http://hyperphysics.phy-astr.gsu.edu/. 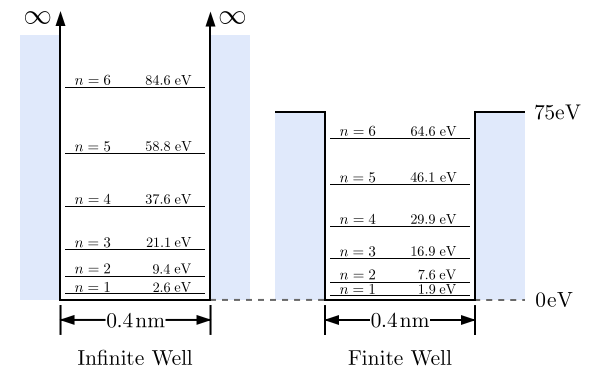
-Imagen de Wikibooks: http://en.wikibooks.org/wiki/Materials_in_Electronics/Confined_Particles/1D_Finite_Wells (los valores numéricos corresponden a una elección de origen en el fondo del pozo).
- Expresión de la función de onda en cada zona:
:
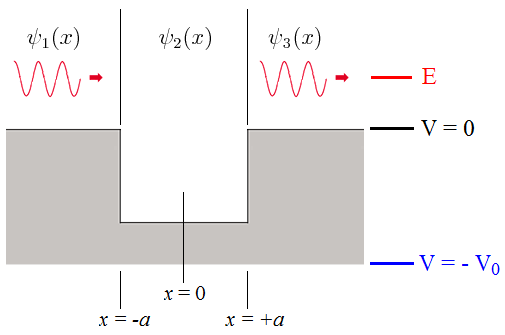
Imagen del blog http://la-mecanica-cuantica.blogspot.com.es/2010/07/transmision-y-reflexion-de-particulas_05.html. - En este caso la función de onda es combinación de funciones oscilatorias en las tres zonas:
conescalares arbitrarios;
.
- Elegimos uno de los dos sentidos de incidencia posibles (según el principio de reciprocidad, los resultados son indiferentes a esta elección); por ejemplo: incidencia desde la izquierda (extremo
), es decir,
.
- Imponiendo las condiciones de contorno:
-Continuidad deen
: (ecuación 1):
-Continuidad deen
: (ecuación 2):
-Continuidad deen
: (ecuación 3):
-Continuidad deen
: (ecuación 4):
- Cálculos:
-A partir de las ecuaciones 3 y 4:
-A partir de la ecuación 2, introduciendo en ella las expresiones paray
anteriores:
(ecuación 5)
-A partir de la ecuación 1, introduciendo en ella las expresiones paray
anteriores:
(ecuación 6)
-Restando de la ecuación 6 la ecuación 5:
-Simplificando, la anterior expresión conduce a: (ecuación 7):
-Sustituyendo la expresión 7 en la anterior 6, se obtiene a continuación: (ecuación 8):
-Las anteriores expresiones 8 y 7 nos permiten a su vez determinar los cocientesy
, cuyos módulos al cuadrado proporcionan finalmente los coeficientes de reflexión y transmisión.
- Función de onda:
- En este caso la función de onda es combinación de funciones oscilatorias en las tres zonas:
- En este caso
, los coeficientes de reflexión
y transmisión
valen:
- Coeficiente de reflexión:
-Por tanto, el coeficiente es en general mayor que cero: puede producirse reflexión, frente a la predicción de física de partículas clásica: a veces una partícula asociada a una autofunción de energía para autovalorno es transmitida y no puede ser localizada en la región III.
- Coeficiente de transmisión:
, es decir, el coeficiente de transmisión puede ser en algunos casos inferior a la unidad.
-La siguientes figura ilustra el comportamiento del coeficiente de transmisión: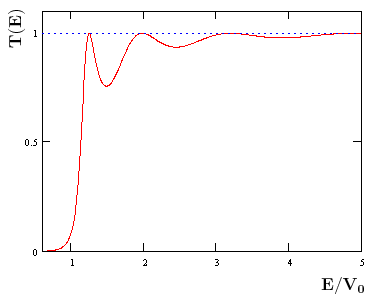
Imagen del blog http://la-mecanica-cuantica.blogspot.com.es/2010/07/transmision-y-reflexion-de-particulas_05.html. -Propiedades:
- El coeficiente
toma un valor nulo cuando
.
- Al aumentar
, presenta oscilaciones, tendiendo asintóticamente al valor unidad cuando
.
- La transmisión es total (certeza de llegar a la región III, es decir, probabilidad cero de reflexión), cuando:
.
-Es decir: no hay reflexión cuando la anchura del pozoes un número semientero o entero de veces la longitud de onda de de Broglie asociada a la partícula en la zona II o zona que abarca el pozo.
- El coeficiente de transmisión alcanza los mínimos de sus fluctuaciones en los valores
.
- En el caso de un pozo muy profundo y un valor
positivo pero pequeño, el factor de transmisión presenta fuertes oscilaciones, siendo pequeño excepto en los máximos señalados:
- El coeficiente
- Coeficiente de reflexión:
- Conforme al principio de reciprocidad, los resultados que se obtienen considerando incidencia desde la derecha (extremo
) son por completo análogos: basta tomar
y proceder en consecuencia.
- En resumen: hemos encontrado dos soluciones linealmente independientes
en el rango
, de forma que todos estos puntos reales pertenecen a la parte continua del espectro
y son doblemente degenerados (en este rango de energías el problema de autovalores tiene dos soluciones linealmente independientes y físicamente aceptable, que se pueden escoger como las correspondientes a sendas incidencias desde la izquierda y desde la derecha).
- La siguiente figura representa el factor de transmisión para un pozo de profundidad
:
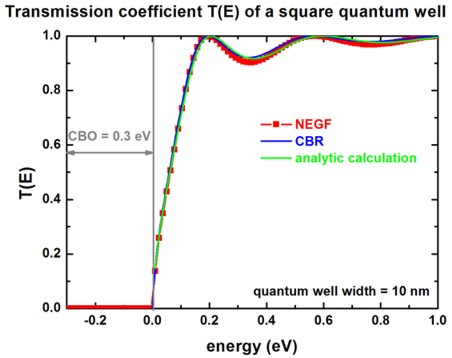
Imagen de http://www.nextnano.de/nextnano3/tutorial/1Dtutorial_Transmission_NEGF.htm . - En el problema estudiado, Hamiltoniano del pozo cuadrado finito, resulta por tanto:
, donde la parte discreta contiene un número finito de valores discretos de energía, correspondientes a los estados ligados y pertenecientes al intervalo
; estos estados poseen paridad definida y no presentan degeneración, satisfaciéndose el teorema de oscilación. La parte continua incluye la semirrecta real positiva y todos los valores de energía en el continuo
son doblemente degenerados.
Referencias
[BOH-89] Bohm, D.; «Quantum Theory»; Dover; New York, 1989.
[BRA-00] Bransden, B.H. and Joachain, C.J.; «Quantum Mechanics»; 2nd ed., Pearson; Dorchester, 2000.
[GAL-89] Galindo, A. y Pascual, P.; «Mecánica Cuántica», Eudema, 1989.
[SCH-68] Schiff,L.I.; «Quantum Mechanics»; 3º ed., McGraw; 1968.
Páginas complementarias
http://la-mecanica-cuantica.blogspot.com.es/2010/07/transmision-y-reflexion-de-particulas_05.html
http://en.wikibooks.org/wiki/Materials_in_Electronics/Confined_Particles/1D_Finite_Wells
http://www.uco.es/hbarra/index.php/fc/apuntesfc/334-fc0303
APPS
http://www.sc.ehu.es/sbweb/fisica/cuantica/pozo/pozo.htm
http://www.uco.es/hbarra/index.php/fc/appletsfc/72-pozo-finito
http://www.st-andrews.ac.uk/physics/quvis/embed_item_3.php?anim_id=19&file_sys=index_phys
http://www.st-andrews.ac.uk/physics/quvis/embed_item_3.php?anim_id=18&file_sys=index_phys
- Vídeo en YouTube para un paquete de ondas incidiendo sobre un pozo de potencial finito:
–https://youtu.be/cV2fkDscwvY (varios casos, primero un pozo finito y luego una barrera):
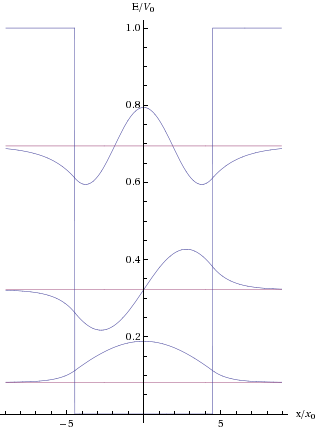
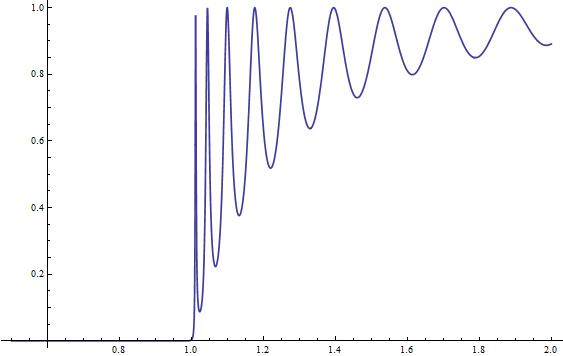
Dejar una contestacion