La detección sin interacción de Elitzur y Vaidman

Medida sin interacción

Fuente: entrada basada en el artículo:

P. Kwiat, H. Weinfurter y A. Zeilinger, Visión cuántica en la oscuridad, Investigación y Ciencia, Temas 10, pp. 91-97.

P. Kwiat, H. Weinfurter y A. Zeilinger, Quantum seeing in the dark, Scientific American, Nov. 1996, p. 52, DOI: 10.1038/SCIENTIFICAMERICAN1196-72 1 (y desde Semantic Scholar).

P.G. Kwiat, H. Weinfurter, T. Herzog, A. Zeilinger and M.A. Kasevich, Interaction-free measurement, Physical Review Letters 74 (1995) 4763.

¿Es posible detectar la presencia de un objeto «sin que se produzca una interacción con él»? (es decir, sin hacer colisionar con él al menos un cuanto de energía: esta terminología, usual en el campo, es bastante discutible y problemática).

En 1993, A. Elitzur y L. Vaidman propusieron el siguiente problema:
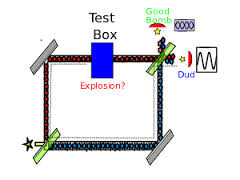
¿cómo saber si hay una bomba oculta, que detona con la mínima interacción, sin arriesgarse a su explosión?
-o, con menos dramatismo:

¿cómo averiguar si hay una piedra en un camino sin tropezar con ella?

A. C. Elitzur and L. Vaidman, Foundations of Physics 23 (1993) 987.

L. Vaidman: Interaction-free measurements (1996) arXiv:quant-ph/9610033; The meaning of The Interaction-Free measurements (2001), arxiv.org/abs/quant-ph/0103081; The Elitzur-Vaidman Interaction-Free Measurements (2008), arxiv.org/abs/0801.2777.

R.H. Dicke, Interaction‐free quantum measurements: A paradox?, American Journal of Physics, 49 (1981) 925.

A.G. White, J.R. Mitchell, O. Nairz and P.G. Kwiat, Interaction free-Imaging, arxiv.org/pdf/quant-ph/9803060v2.pdf

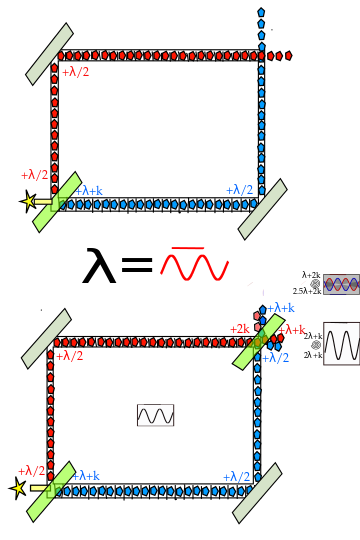
Recordemos el montaje de la doble rendija a la Mach-Zehnder:

El montaje equivale a la doble rendija: además, ajustando convenientemente la fase entre los caminos ópticos, con interferencias (caminos indistinguibles, «dos caminos»), puede conseguirse que sólo 1 detector específico señale (siempre el mismo, el D-Luz; al otro detector, el D-oscuridad, nunca llega señal); con detección de camino (sin segundo divisor: caminos distinguibles, «un camino»), la luz alcanza los dos, al 50% aleatorio, nunca a la vez (también fotón a fotón).

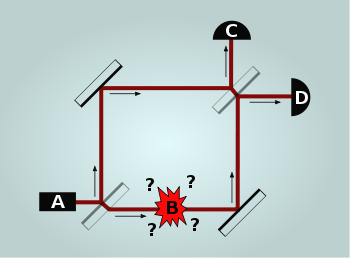
-Supongamos ahora que en el montaje interferencial, con los dos divisores de haz presentes y en acción, un obstáculo se interpone en uno de los dos caminos o brazos del interferómetro:

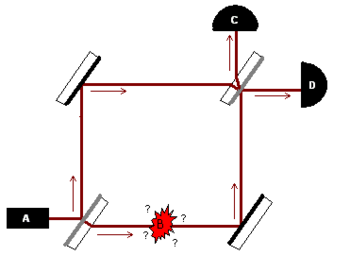
Con el obstáculo interpuesto, los caminos son distinguibles: por tanto, el fotón «elige sólo uno de los dos caminos» (¡se trata sólo de un RELATO!) y no se producen interferencias.

-En el 50% de los casos, el fotón elige el camino de la piedra y tropieza (la bomba explota), no llegando a ningún detector: no útil.

-En el otro 50%, la mitad de las veces el fotón elige el camino sin obstáculos, y, puesto que ya no hay interferencias, al tener caminos distinguibles, el segundo divisor lo manda, aleatoriamente, a uno de los dos detectores (25% para cada uno del total).
-Si va al detector-luz, el procedimiento no es útil: habría llegado a él también sin obstáculo.

Pero en el 25% de los casos restantes, en que el fotón llega al detector-oscuridad, habiendo ido por el camino despejado, entonces sabemos, ¡sin interacción alguna!, que había un obstáculo en el camino.

Un experimento realizado:

P. Kwiat, H. Weinfurter, T. Herzog and A. Zeilinger, Interaction-Free Measurement, Phys. Rev. Lett. 74 (1995) 4763.

-Nota: Se consigue pasar del 25%, hasta un 50%, usando un divisor sin apenas reflexión, haciendo intervenir el «efecto Zenón cuántico»,

Experimento de efecto Zenón con iones de berilio: W.M. Itano, D.J. Heinzen, J.J. Bollinger and D.J. Wineland, Quantum Zeno effect, Physical Review A41-5 (1990) 2295-2300: https://tf.nist.gov/general/pdf/858.pdf.

La medición afecta al resultado, de modo que un sistema cuántico puede quedar atrapado en su estado inicial, aun cuando dejado a su aire hubiera evolucionado hacia otro; véase también de nuevo:
P. Kwiat, H. Weinfurter y A. Zeilinger, Visión cuántica en la oscuridad, Investigación y Ciencia, Temas 10, pp. 91-97; versión americana: P.G. Kwiat, H. Weinfurter y A. Zeilinger, Quantum seeing in the dark, Scientific American, Nov. 1996, p. 52, DOI: 10.1038/SCIENTIFICAMERICAN1196-72 1 (y desde Semantic Scholar).

Aplicaciones:

–Fotografías sin exponer los objetos a la luz:
(¿radiografías sin irradiar a los pacientes?… ¡improbable por las $\lambda$ involucradas!).

A.G. White, J.R. Mitchell, O. Nairz and P.G. Kwiat: «Interaction-free» imaging: Phys. Rev. A 58 (1998) 605-613.

Abstract: Using the complementary wavelike and particle-like natures of photons, it is possible to make «interaction-free» measurements where the presence of an object can be determined with no photons being absorbed. We investigated several «interaction-free» ‘imaging’ systems, i.e., systems that allow optical imaging of photosensitive objects with less than the classically expected amount of light being absorbed or scattered by the object. With the most promising system, we obtained high-resolution (10- $\mu$ m), one-dimensional profiles of a variety of objects (human hair, glass and metal wires, and cloth fibers) by raster scanning each object through the system. We discuss possible applications and the present and future limits for interaction-free imaging.

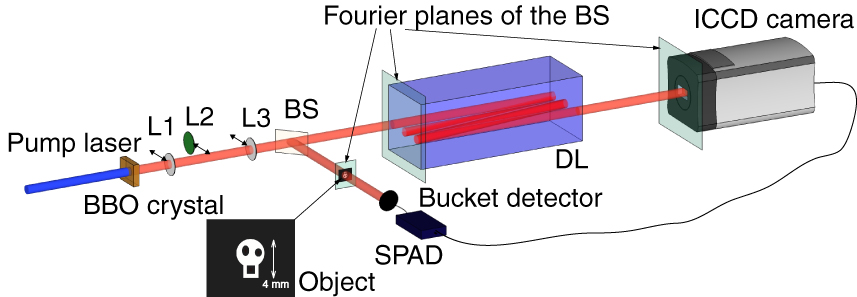
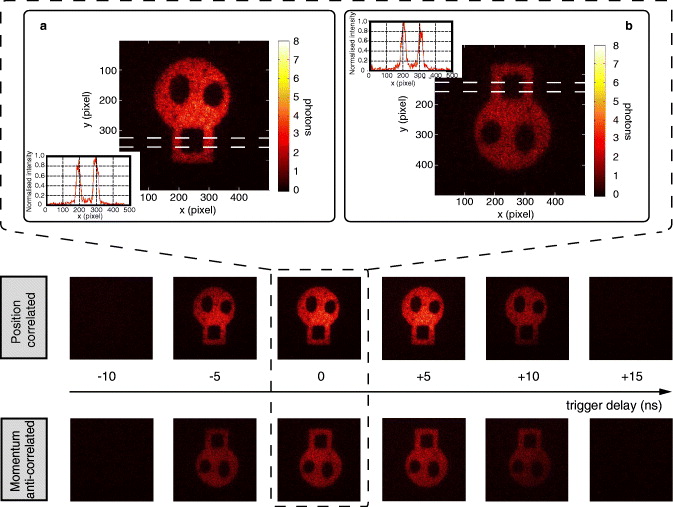
R.S. Aspden, D.S. Tasca, R.W. Boyd and M.J. Padgett: EPR-based ghost imaging using a single-photon-sensitive camera ; New Journal of Physics (open access):

Abstract: Correlated photon imaging, popularly known as ghost imaging, is a technique whereby an image is formed from light that has never interacted with the object. In ghost imaging experiments, two correlated light fields are produced. One of these fields illuminates the object, and the other field is measured by a spatially resolving detector. In the quantum regime, these correlated light fields are produced by entangled photons created by spontaneous parametric down-conversion. To date, all correlated photon ghost imaging experiments have scanned a single-pixel detector through the field of view to obtain spatial information. However, scanning leads to poor sampling efficiency, which scales inversely with the number of pixels, N, in the image. In this work, we overcome this limitation by using a time-gated camera to record the single-photon events across the full scene. We obtain high-contrast images, 90%, in either the image plane or the far field of the photon pair source, taking advantage of the Einstein-Podolsky-Rosen-like correlations in position and momentum of the photon pairs. Our images contain a large number of modes, >500, creating opportunities in low-light-level imaging and in quantum information processing.

Imágenes sacadas de la referencia:

Imágenes sin interacción — Figure 1. Schematic diagram of the experimental setup. Collinear down-converted photon pairs at 710 nm are generated by pumping a β-barium borate (BBO) crystal with a UV laser at 355 nm. L1 and L3 are 50 mm focal length lenses used to produce an image of the down-conversion source onto the beam splitter (BS). L2 is a 100 mm focal length lens used to Fourier transform the exit facet of the down-conversion source onto the BS. A 300 mm focal length lens (not shown) is used after the BS in each path to Fourier transform the down-converted fields at the BS onto the planes of the object in one arm and onto the input plane of an image preserving DL in the other arm. The image preserving DL consists of seven imaging systems with a total length of 22 m. Our object (inset) is a transmissive mask with the shape of a skull printed on acetate. Fuente: https://iopscience.iop.org/article/10.1088/1367-2630/15/7/073032/meta

Figure 2. Ghost images and trigger delay timing. Ghost images obtained in the position correlated and momentum anti-correlated configurations as a function of the trigger delay, with a total integration time of 1 h per image. The delay is scanned in increments of 5 ns, which corresponds to adding/removing 1 m of cable. The images shown in (a) and (b) are enlarged versions of the images obtained with optimum delay time, for which the total number of photo-events was 124 310 and 74 021, respectively. The insets show cross-sections of the images averaged over the 30 rows indicated by the dashed lines. Fuente: https://iopscience.iop.org/article/10.1088/1367-2630/15/7/073032/meta

Bibliografía

P.G. Kwiat, H. Weinfurter y A. Zeilinger, Visión cuántica en la oscuridad, Investigación y Ciencia, Temas 10, pp. 91-97.

P.G. Kwiat, H. Weinfurter y A. Zeilinger, Quantum seeing in the dark, Scientific American, Nov. 1996, p. 52, DOI: 10.1038/SCIENTIFICAMERICAN1196-72 1 (y desde Semantic Scholar<

Una divulgación completa: http://eltamiz.com/2010/07/21/cuantica-sin-formulas-el-detector-de-bombas-de-elitzur-vaidman/

Seminario divulgativo en la Univ. Nacional de Córdoba, por G.A. Álvarez:sobre como Perseo pudiera haber visto a Medusa

Artículo en la Wikipedia en español: Detector de bombas de Elitzur-Vaidman

Física cuántica en la red

Un sitio para adentrarse en la física cuántica

La detección sin interacción de Elitzur y Vaidman

Sé el primero en comentar

Dejar una contestacion Cancelar la respuesta