De Broglie: las ondas de materia

ondas-materia-difraccion-electrones-art04fig3-210x126

*Imagen procedente de: http://www.quotespin.com.*

Ondas de materia

En 1924 L. de Broglie presenta su Tesis Doctoral, en la cual postula las ondas de materia.
Precedentes:
1. a) La analogía de Hamilton: En 1833, Hamilton había propuesto dotar a la óptica de un formalismo semejante al de la mecánica analítica, vía la analogía entre:
  1. La cantidad mecánica $\frac{1}{p} = \frac{1}{\sqrt{2m(E - V)}}$ , en la expresión del principio de P. L. Maupertuis para una partícula de masa $m$ y energía total $E$ en un campo de fuerzas de energía potencial $V$ , o principio de mínima acción (1744): la trayectoria seguida por una partícula es la que hace estacionaria la acción: $\delta \int_A^B \sqrt{2m(E-V(\vec{r}))}ds= \int_A^B p(\vec{r})ds=0$ .
  2. La cantidad óptica $\lambda$ del principio de Fermat (1657): la trayectoria seguida por un rayo de luz monocromático es la que hace estacionario el camino óptico: $\delta \int_A^B \frac{ds}{\lambda (\vec{r})}ds=0$ .
  - Se establece, pues, una correspondencia entre cada magnitud de la mecánica y de la óptica geométrica: trayectoria de la partícula/rayo de luz; superficie de acción constante/superficie de onda.
  - Si la óptica geométrica es una aproximación de la óptica ondulatoria en el límite de las pequeñas longitudes de onda, se intuye que la mecánica clásica es una aproximación a una «mecánica ondulatoria» en el límite en que las longitudes de onda asociadas, que de Broglie va a introducir, tienden a cero (también: en el límite macroscópico $h \rightarrow 0$ ).
2. b) Los trabajos de M. Brillouin: en sus estudios sobre el movimiento vibracional de una partícula en un medio elástico, había realizado una comparación con el modelo atómico de Bohr, caracterizando las propiedades discontinuas por números enteros.

La Tesis Doctoral de L. de Broglie
- Broglie, L. de; «Recherches sur la théorie des quanta», Annales de Physique 10,3 (1925) 22-128.
- La tesis es una versión integrada de diversos artículos aparecidos entre 1922 y 1924, y en ella de Broglie establece la «dualidad onda-corpúsculo» para las partículas materiales.
- Hipótesis: la idea básica de la teoría cuántica es la imposibilidad de considerar «una porción aislada de energía» sin asignarle una frecuencia $\nu$ : apelación a la relación de Einstein $E=h \nu$ de los cuantos de luz (fotones).
- Tesis: Las partículas materiales, también «porciones aisladas de energía», debería ser tratadas análogamente, asociándoles una longitud de onda $\lambda$ : relación de de Broglie $\lambda = \frac{h}{p}$ (postulación de las ondas de fase o materia).
- La hipótesis no se acompañaba de ninguna interpretación. Todo lo más, afirmaba de Broglie, podría tratarse de «algún movimiento periódico interno desconocido».
- Esquema de la Tesis:
  1. Cap. 1: Justificación de la introducción de la onda de fase o materia y discusión de sus propiedades, demostrándose la igualdad entre la velocidad de grupo y la de la partícula.
  2. Cap. 2: Análisis de los principios de Fermat y Maupertuis, aplicados a la descripción de la partícula cuántica: «El principio de Fermat aplicado a la onda de fase es idéntico al principio de Mauterpuis aplicado a la partícula; las trayectorias dinámicamente posibles para la partícula son idénticas a los rayos posibles para la onda».
  3. Cap. 3: Estudio de las condiciones cuánticas de la estabilidad de las órbitas electrónicas en los átomos; se impone la condición de resonancia $long=n \cdot \lambda$ , donde $long$ es la longitud de la órbita, y se obtienen las condiciones de cuantización de Bohr-Sommerfeld.
  4. Cap. 4: Aplicación de la condición de resonancia al átomo de hidrógeno relativista.
  5. Cap. 5: Mediante los cuantos de luz, supuestos de masa extraordinariamente pequeña, se justifican con la teoría corpuscular de la luz los efectos Doppler y otros.
  6. Cap. 6: Estudio de la dispersión de rayos X y $\gamma$ por la materia; análisis del efecto Compton.
  7. Cap. 7: Desarrollo de una mecánica estadística de los cuantos de luz y átomos.
- Hay que destacar que en 1923 de Broglie ya había sugerido la posibilidad de observar fenómenos de difracción con sus ondas de fase. Asimismo, en la lectura de su tesis, a preguntas de Perrin, miembro del Tribunal de evaluación de la Tesis, afirmó que podría realizarse mediante la difracción de electrones por cristales. Tales experimentos serían llevados a cabo en 1927 por Davisson y Germer e, independientemente, por Thomson.
- Comentemos, finalmente, que Langevin, también miembro del Tribunal, haría llegar una copia de la tesis a Einstein, quien comentó muy favorablemente su contenido al propio Langevin y a Lorentz.
En 1929 recibiría el premio Nobel por este trabajo; su discurso de recepción puede leerse en: http://www.nobelprize.org/nobel_prizes/physics/laureates/1929/broglie-lecture.pdf .
La hipótesis de de Broglie puede afirmarse como la de una simetría: si un cuanto de luz de frecuencia $\nu$ posee energía $h\nu$ (Einstein, 1905) y momento $p=\frac{h\nu}{c}$ (Stark 1909; Einstein, 1916-17), entonces una partícula material de masa en reposo $m_0 \ne 0$ , energía y masa relativistas $E$ , $m=\frac{m_0}{\sqrt{1-\frac{v^2}{c^2}}}$ , posee asociada una onda de longitud $\lambda=\frac{h}{p}=\frac{h}{mv}=\frac{h\sqrt{1-\frac{v^2}{c^2}}}{m_0v}$ y frecuencia $\nu=\frac{E}{h}=\frac{m_0c^2}{h\sqrt{1-\frac{v^2}{c^2}}}$ .
Los siguientes ejemplos proporcionan una idea del orden de magnitud involucrado para la onda y longitud de onda de de Broglie de una partícula con diferentes valores de momento:
1. Para $m=46\,g$ , $v=30\,m/s$ , se tiene $\lambda=4,8\times 10^{-34}m$ (pelota de golf; $\lambda$ inobservable).
2. Para $m_e=9,1\times 10^{-31}\,kg$ , $v=10^7\,m/s$ , se tiene $\lambda=7,3\times 10^{-11}m$ (electrón; $\lambda$ observable con la adecuada red de difracción).
3. Para $m_e=9,1\times 10^{-31}\,kg$ , $v=\sqrt{\frac{2eV}{m_e}}$ , se tiene $\lambda=\frac{h}{\sqrt{2m_e eV}}\approx \frac{12,25\AA}{\sqrt{V(voltios)}}$ (electrón no relativista acelerado por una diferencia de potencial $V$ voltios hasta la energía $E=eV=1,6\times 10^{-19}C\cdot V$ ); para potenciales $V$ de pocos $V$ se obtienen longitudes $\lambda$ en el rango de los rayos $X$ : por ejemplo, para $V\approx 15 000V \rightarrow \lambda \approx 0,1\,\AA$ ; para $V=100V \rightarrow \lambda = 1,225\,\AA$ .

Formulario (partícula material)

$\lambda=\frac{h}{p}$ ; ( $\nu=\frac{E}{h}$ )

$\omega=2\pi \nu$ ; $k=\frac{2\pi}{\lambda}$

Dominio relativista	Aproximación no relativista	Comentarios
$E_r^2=m_0^2c^4+p_r^2c^2=m^2c^4$	$E_{nr}=\frac{p_{nr}^2}{2m_0}=K_{nr}$	(es usual ignorar la energía en reposo $m_0c^2$ en $E_{nr}$ )
$p_r=mv=\frac{m_0v}{\sqrt{1-\frac{v^2}{c^2}}}$	$p_{nr}=m_0v$
$K_r=E_r-m_0c^2$	$K_{nr}=E_{nr}=\frac{p_{nr}^2}{2m_0}=\frac{1}{2}m_0v^2$

$\lambda_r=\frac{h}{p_r}=\frac{h}{mv}=\frac{h\sqrt{1-\frac{v^2}{c^2}}}{m_0v}$	$\lambda_{nr}=\frac{h}{p_{nr}}=\frac{h}{m_0v}$
$\nu=\frac{mc^2}{h}=\frac{m_0c^2}{h\sqrt{1-\frac{v^2}{c^2}}}$
$\nu=\frac{+\sqrt{m_0^2c^4+p_r^2c^2}}{h}=\frac{mc^2}{h}$	Nota: $lim_{v < < c}\nu=\frac{m_0c^2}{h}=\nu_0$	( $\nu$ sin significado físico: origen arbitrario de energías)
$h^2\nu^2\lambda^2=m_0^2c^4\lambda^2 + h^2c^2$
En general:
$E=h\nu =\hbar \omega$ $\vec{p}=\hbar \vec{k}$		( $k=\frac{2\pi}{\lambda}$ es el número de ondas)
$v_B=\nu \lambda=\frac{\omega}{k} =\frac{2\pi mv}{h}=\frac{2\pi m_0v}{h\sqrt{1-\frac{v^2}{c^2}}}$ $\omega=2\pi \nu=\frac{2\pi}{T}=\frac{\hbar k^2}{2m}$
$v_g=\frac{d \omega}{d k}=v$ $\frac{1}{v_g}=\frac{d}{d\nu}(\frac{1}{\lambda})=\frac{dp}{dE}=\frac{1}{v}$ $(p^2=\frac{E^2}{c^2}-m_0^2c^2)$		(la veloc. de grupo $v_g$ coincide con la veloc. $v$ de la partícula )	( $v_B=\frac{v_g}{2}$ para un «paquete de ondas»)

Frente a la frontal oposición que encontrara el cuanto de luz en 1905, de lo que puede dar idea el que se necesitaran años para pasar de la expresión para su energía a la que les asignaba definitivamente también momento (Stark, 1909; Einstein, 1916), la hipótesis de De Broglie recibiría confirmación experimental en menos de tres años, cuando en 1927 se realizaron los primeros experimentos de difracción de electrones por redes cristalinas.

Justificación de las reglas de cuantización

En el momento en que De Broglie postuló las ondas de materia, no se disponía de ningún apoyo experimental a su hipótesis, pero sí que fue capaz de mostrar cómo su conjetura era capaz de justificar teóricamente las reglas de cuantización disponibles y, por tanto, la cuantización de los niveles de energía en los modelos atómicos primitivos, como los de Bohr y Sommerfeld-Wilson.
Así, la condición de cuantización de Bohr para el momento angular orbital, $L=mvr=n\hbar$ , puede expresarse como la condición $L=pr=\frac{h}{\lambda}r=n\frac{h}{2\pi}$ , de donde se deriva que $n\lambda=2\pi r$ , es decir: las órbitas permitidas en el modelo atómico de Bohr son las que poseen una longitud que es múltiplo entero de la longitud de onda de de Broglie asociada al electrón en dicha órbita. Para otras longitudes de onda, se producirá interferencia destructiva y la onda no perdurará.
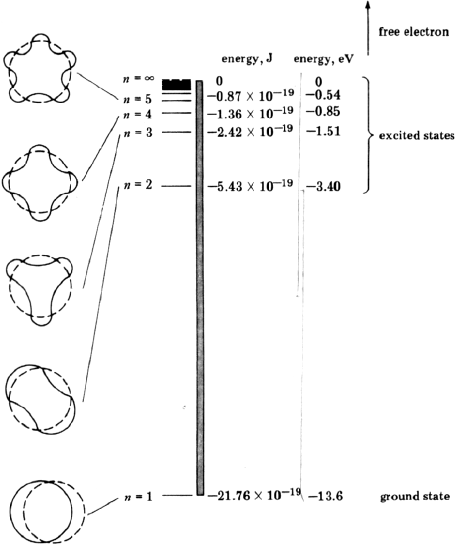
La imagen evocada es pues la que asimila el conjunto de niveles de energía permitidos con un conjunto de ondas estacionarias, que oscilan indefinidamente en ausencia de perturbación externa y cuyas frecuencias pueden ser tan sólo un conjunto determinado.
Una explicación análoga se aplica a las reglas de cuantización de Sommerfeld-Wilson-Ishiwara para un sistema multiperiódico de grados de libertad, descrito por las coordenadas generalizadas y los correspondientes momentos generalizados , los cuales supondremos que, sobre cada trayectoria en el espacio de las fases, pueden expresarse como funciones que dependen exclusivamente de la coordenada correspondiente, esto es, .
- Según las condiciones indicadas, la función Hamiltoniana del sistema puede escribirse en términos de las variables de acción $J_1,\ldots,J_m$ , definidas según $\oint p_idq_i$ , donde la integral se extiende a un período completo de la variable $q_i$ , de forma que $J_i$ sólo está definido si el sistema es en efecto periódico en la variable $q_i$ , teniéndose entonces $H=H(J_1,\ldots,J_m)$ .
- Las variables de acción $J_i$ son constantes del movimiento, viniendo dada la frecuencia de cada movimiento por $\nu_i=\frac{\partial H}{\partial J_i}\,;\,i=1,\ldots,m$ .
- Las reglas de cuantización S-W-I establecen que las variables de acción $J_i$ están cuantizadas: sólo pueden tomar los valores que cumplen la condición $J_i=\oint p_idq_i=n_ih\,,\,i=1,\ldots,m\,,\,n_i=0,1,2\ldots$ , donde los $n_i$ representan los distintos números cuánticos así introducidos.
- Es decir: en una ruptura con la Física Clásica, donde las variables de acción toman valores sobre un rango continuo, según las reglas S-W-I sólo pueden tomar valores discretos, siendo la constante $h$ de Planck la que determina el tamaño de la discretización establecida, es decir, el cuanto elemental de acción.
- Por ejemplo, si consideramos el caso sencillo de una partícula libre realizando un movimiento periódico a lo largo del eje $OX$ entre dos paredes impenetrables situadas en las posiciones $x=\pm \frac{d}{2}$ , las reglas de cuantización imponen $J=\oint p_xdx=p_x\oint dx=2p_xd=nh\,,\,n=1,2\ldots$ (al moverse libremente, el módulo del momento se mantiene constante, no así su sentido); por tanto, se obtiene la cuantización $p_x=\frac{nh}{2d}$ y $E=\frac{p_x^2}{2m}=\frac{n^2h^2}{8md^2}$ .
- Incorporando la hipótesis de De Broglie, la onda asociada tendrá una longitud $\lambda=\frac{h}{p_x}=\frac{h2d}{nh}$ , por lo que se deriva $n\lambda=2d$ : la cavidad ha de contener un número entero de semi-longitudes de onda. Esta condición es análoga a la que rige la formación de ondas estacionarias en una cuerda en que se mantienen fijos los extremos: sólo están permitidas determinadas frecuencias de vibración.

Experimento de Davisson-Germer

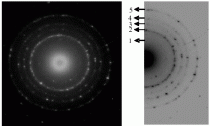
En 1927 G.P. Thomson, en Inglaterra, y C.G. Davisson y L. Germer, en Estados Unidos, realizaron trabajos experimentales independientes con los que confirmaron la existencia de las ondas de de Broglie, al comprobar la difracción de electrones por redes cristalinas (por ello, Thomson y Davisson compartieron el Nobel de 1937).
El investigar la naturaleza ondulatoria de la materia mediante experimentos de difracción por cristales fue sugerido en 1926 por W. Elsasser, en analogía a lo que se había hecho con los rayos-X para establecer su naturaleza ondulatoria y determinar su longitud de onda. Puesto que los efectos de difracción aparecen cuando la dimensión característica de la abertura difractante es de un orden de magnitud similar al de la longitud de onda de la radiación incidente, los cristales con parámetros de red del orden del $\AA$ aparecen como idóneos para experimentar la difracción de partículas materiales como electrones acelerados por potenciales de decenas de Voltios.
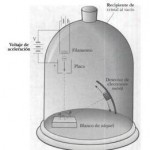
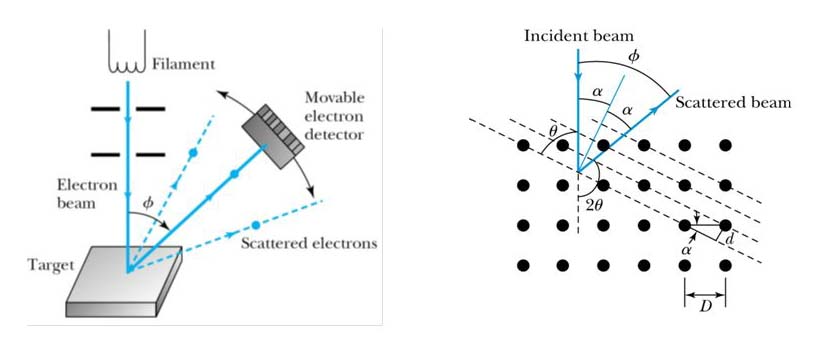
Davisson y Germer, en los laboratorios de la compañía Bell Telephones, utilizaron un dispositivo en que los electrones eran emitidos por un filamento de Wolframio calentado (emisión termoiónica), acelerados por una diferencia de potencial $V$ del orden de los $50\,V$ y lanzados en incidencia normal contra un cristal de Níquel, que posee una estructura cúbica. La anécdota es que, de hecho, parece que el objetivo inicial del experimento era el estudio de este elemento, que convirtieron en forma monocristalina por accidente: después de una ruptura accidental de la bomba de vacío, se formó una capa de óxido sobre el níquel en el blanco; para removerla, lo introdujeron en un horno, donde la elevada temperatura produjo su recristalización, pasando de una forma policristalina inicial a otra monocristalina, con la aparición de los denominados planos de Bragg atómicos.
Dispositivo de Davisson-Germer (imagen de Roshan, Wiki Commons, licencia GNU).
El dispositivo permitía medir la distribución angular del haz emergente o electrones reflejados, a través de la intensidad de la corriente medida en el detector en función del ángulo $\theta$ ; el sistema era mantenido en alto vacío para evitar colisiones de los electrones con otras moléculas interpuestas en su desplazamiento hacia el blanco.
Usando el Níquel fortuitamente monocristalizado (en un corte tal que, para una incidencia normal del haz de electrones sobre el blanco, por la disposición de los planos atómicos el ángulo de incidencia a considerar no es el recto, ver las dos figuras siguientes para la notación de ángulos), encontraron que la distribución angular de los electrones dispersados mostraba máximos y mínimos dependiendo del ángulo de esparcimiento, de una forma muy similar a los resultados conocidos para los rayos $X$ y justificados por la ley de Bragg, $n\lambda=2dsen\theta\,,\,n=0,1,2, \ldots , 2 \frac{d}{\lambda}$ .
Según la predicción clásica, los electrones difundidos deben emerger en todas las direcciones, con una moderada dependencia de la intensidad con el ángulo, menor aún con respecto a su energía.
En cambio, si se acepta la hipótesis de de Broglie, y se considera la longitud de onda asociada, $\lambda=\frac{h}{p}=\frac{h}{\sqrt{2m_e E}}=\frac{h}{\sqrt{2m_e eV}}\approx \frac{12,25\AA}{\sqrt{V(voltios)}}$ (electrón no relativista acelerado por una diferencia de potencial de $V$ voltios), el experimento puede considerarse por completo equivalente al proceso de dispersión de rayos $X$ por un cristal, donde la condición de Brag, $n\lambda=2dsen\theta\,,\,n=0,1,2\ldots$ , define las direcciones para las que los haces elementales reflejados por los distintos planos atómicos interfieren constructivamente entre sí, dando lugar a un máximo de intensidad:
Figura 1: esquema de una difracción en planos de Bragg.

Figura 2: corte oblicuo de planos de Bragg.
Para las restantes direcciones, es decir, para otros ángulos de incidencia del haz, la interferencia resultante entre los distintos haces difundidos es predominantemente destructiva y la intensidad del haz dispersado, en consecuencia, prácticamente nula.
Por tanto, si la hipótesis de Broglie es correcta, la distribución angular debía dar precisamente el resultado que Davisson y Germer obtuvieron: una función que presenta máximos y mínimos acusados:
1. Resultado para electrones acelerados por una diferencia de potencial de $V=54\,V$ a los que se les asocia una longitud de onda de de Broglie de $\lambda=1,667\,\AA$ : la distribución angular presenta un máximo para el ángulo de esparcimiento $\phi=50^o$ , correspondiente por el corte del cristal blanco empleado a un ángulo de incidencia $\alpha=25^o$ y al ángulo de dispersión $\theta=\frac{\pi - \phi}{2}=65^o$ , el cual, según la condición de Bragg, puesto que para el Níquel $d=0,91\,\AA$ , en el primer orden de difracción ( $n=1$ ) corresponde a una longitud de onda de $\lambda=1,649\,\AA$ :
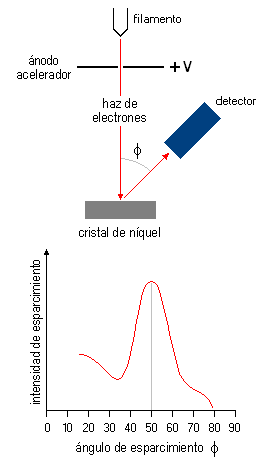
  Imagen tomada del blog: http://la-mecanica-cuantica.blogspot.com.es/ 2009/08/ondas-de-materia.html.
  
  Nota: sobre los distintos ángulos y su notación: $\alpha$ es el ángulo de incidencia, o ángulo del haz incidente con la normal a los planos atómicos de Bragg; en la figura 2 anterior: $\theta + \alpha=\frac{\pi}{2}$ ; $\phi=2\alpha\,,\, \alpha=\frac{\pi}{2}-\theta$ ; $\phi$ es el ángulo de esparcimiento, o ángulo entre la radiación incidente y la dispersada.
2. Diagramas polares. Las siguientes figuras muestran los denominados diagramas polares, en los que la intensidad para cada valor del ángulo de esparcimiento $\phi$ se representa proporcionalmente: sobre cada dirección marcada por las rectas que pasan por el origen, formando un ángulo $\phi$ con el eje vertical, se toma un segmento de longitud proporcional a la intensidad del haz difundido para dicho valor de ángulo, para un $V$ fijo (y, por tanto, para una $\lambda$ asociada dada); destaca el acusado pico, máximo absoluto, en la gráfica c, correspondiente a los valores $V=54\,V$ y $\phi=50^o$ :
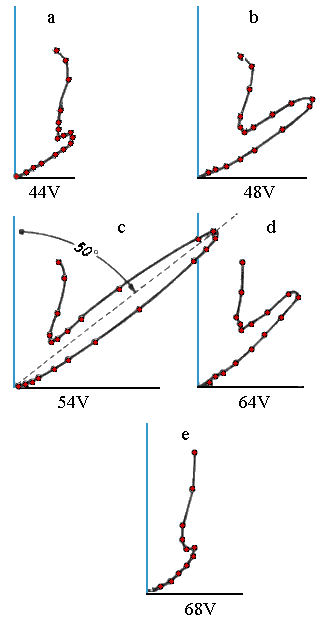
  Diagramas polares en un experimento de Davisson-Germer (imagen procedente del blog: www.la-mecanica-cuantica.blogspot.com).
3. Recuérdese que, 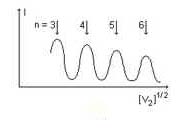según la condición de Bragg, y fijado el valor del potencial $V$ , se observarán, para cada ángulo, una serie de máximos sucesivos, correspondientes a los diferentes órdenes o valores $n=0,1,2,3\ldots$ La figura a la derecha muestra los sucesivos máximos observados para un valor de $\theta=80^o$ . Es interesante indicar que, ante la dificultad de operar moviendo el blanco, lo que se hacía era, manteniéndolo fijo, medir la dispersión para un ángulo $\theta$ también fijo, variando continuamente el potencial acelerado aplicado, generándose así los sucesivos máximos correspondientes a las $\lambda$ que cumplen la condición de Bragg, $n\lambda=2dsen\theta\,,\,n=0,1,2\ldots$ , para los distintos enteros $n$ .
En 1926, en una conferencia científica, Davisson tuvo la sorpresa de ver que sus primeras gráficas publicadas, centradas en el estudio del Níquel, eran esgrimidas por científicos como M. Born en apoyo de la hipótesis de de Broglie, para él desconocida en ese momento: su equipo había sido el primero en superar las dificultades técnicas del montaje requerido. Tras ello, refinaría sus experimentos, obteniendo resultados más precisos y variados con la finalidad de poner a prueba la hipótesis de de Broglie : variaron $V$ y confirmaron la variación de $\lambda$ según la relación de de Broglie $\lambda=\frac{h}{p}$ ; observaron los máximos de los distintos órdenes predichos por la ley de Bragg.
En general, el análisis precedente ha sido simplificado para su exposición: estos experimentos son bastante complejos, pues, además de lo expuesto, requieren incorporar también el papel de la función de trabajo superficial del material en el blanco; la distinta velocidad de los electrones en el cristal respecto al vacío, y las variaciones de velocidad de los distintos electrones según su profundidad en el cristal; las interferencias entre haces difractados por diferentes familias de planos de Bragg, etc.
G. P. Thomson también llevó a cabo en 1927 un experimento que probaría la hipótesis de de Broglie, con un montaje experimental distinto al de Davisson-Germer, en el que se producía la difracción de electrones por hojas metálicas policristalinas, siguiendo la técnica usada anteriormente por Debye, Hull y Scherrer en sus experimentos de difracción de rayos $X$ (ver referencia [SAN-91], pp. 88-89).
Patrón de difracción típico obtenido en un MET, o microscopio electrónico de transmisión, con un haz de electrones paralelo (imagen de Wiki Commons GNU licencia).
La naturaleza ondulatoria de los electrones es
Patrón típico de difracción de electrones por una red cristalina.

el fundamento de los denominados microscopios electrónicos, que empezarían a usarse a partir de 1932. Con ellos se consiguen resoluciones del orden casi del $\AA$ (con electrones acelerados por un potencial $V \approx 100\, keV$ ), lo que supuso un gran avance frente a la resolución máxima de los microscopios ópticos convencionales (unos $2000\, \AA$ aproximadamente); el enfoque se consigue mediante la aplicación de campos electromagnéticos.

Tabla procedente de: http://morfoudec.blogspot.com.es/2008/07/ microscopio-electrnico.html.

Experimentos similares se llevaron a cabo posteriormente con partículas materiales más pesadas que el electrón. Por ejemplo, en 1930-31 Estermann, Stern y Frisch emplearon haces atómicos de Helio y haces moleculares de Hidrógeno, logrando su difracción sobre cristales de fluoruro de Litio, confirmando de nuevo plenamente la hipótesis de de Broglie. También, posteriormente, en 1947, Fermi, Marshall y Zinn demostraron la difracción e interferencia de neutrones lentos.

Como quedó claro en la teoría moderna, la interferencia constructiva que produce el máximo de intensidad observada no ocurre entre las ondas asociadas a diferentes electrones, sino que refiere a la interferencia entre las distintas partes de la onda asociada al electrón. De acuerdo con esta interpretación, y como se comprobaría experimentalmente, si se realiza el experimento con un haz de tan baja intensidad que pueda referirse que los átomos son dispersados de uno en uno, los resultados del experimento se mantienen inalterables.
Finalmente, y conforme al principio de correspondencia, está claro que en el límite $h \rightarrow 0$ , la longitud de onda de de Broglie asociada será tan pequeña que los efectos cuánticos asociados serán despreciables y la Mecánica Clásica será una teoría apropiada para dar cuenta del fenómeno concernido.

Referencias

[BEI-97] Beiser, A.; Concepts of Modern Physics, McGraw-Hill, Singapore, 1997.

[ICA-91] Icaza, J.J.; La construcción de la Mecánica Cuántica, Univ. del País Vasco, Bilbao, 1991.

[MEH-82] Mehra,J., Rechenberg,H.; The Historical Development of Quantum Mechanics, 6 vol., Springer-Verlag, Nueva York, 1982.

[SAN-91] Sánchez del Río, C. (coord.); Física Cuántica (I), Eudema, Madrid, 1991.

-Discurso de L. de Broglie en la recepción del Nobel:

http://www.nobelprize.org/nobel_prizes/physics/laureates/1929/broglie-lecture.pdf

Páginas complementarias

Apuntes de J.I. Fernández Palop: Hipótesis de de Broglie y experimento de Davisson-Germer (pdf).

http://la-mecanica-cuantica.blogspot.com.es/2009/08/ondas-de-materia.html

APPS:

-Ondas de materia (un vídeo de 1961 descargable): http://tsgphysics.mit.edu/front/?page=demo.php&letnum=Z%2047

-Wolfram app:

Electron Waves in Bohr Atom from the Wolfram Demonstrations Project by Ken Caviness.

Física cuántica en la red

Un sitio para adentrarse en la física cuántica

De Broglie: las ondas de materia

1 comentario

Dejar una contestacion Cancelar la respuesta