
Efecto Hanbury Brown-Twiss
Interferómetros estelares
![]() El efecto HB-T se relaciona con las correlaciones medidas entre las intensidades de dos haces de radiación.
El efecto HB-T se relaciona con las correlaciones medidas entre las intensidades de dos haces de radiación.
-Las técnicas anteriores de medida de funciones de correlación se habían enfocado sobre la función de primer orden, esto es, en determinar las correlaciones entre los campos, mediante experimentos que permitían determinar, por ejemplo, el grado de monocromaticidad de una fuente, o la longitud de coherencia de la radiación, pero que no permitían distinguir entre radiaciones que compartiesen distribución espectral pero tuviesen distintas distribuciones fotónicas.
-En la década de los 50, Robert Hanbury Brown y Richard Quintin Twiss desarrollaron en Manchester un nuevo tipo de montaje experimental que exploraba las correlaciones entre las intensidades de la radiación, esto es, determinaba la función de correlación de segundo orden. En 1956, merced a esta nueva técnica, encontraron que, usando dos telescopios que apuntaban a la misma estrella (Sirius), las correspondientes señales de intensidad recogidas exhibían una correlación que permitía determinar los diámetros angulares de la estrella:
![]() Hanbury Brown, R. &. Twiss, R. Q. «Correlation between photons in two coherent beams of light«, Nature 177, 27-29 (1956).
Hanbury Brown, R. &. Twiss, R. Q. «Correlation between photons in two coherent beams of light«, Nature 177, 27-29 (1956).
![]() Hanbury Brown, R. &. Twiss, R. Q. «A test of a new type of stellar interferometer on Sirius«, Nature 178, 1046-1048 (1956).
Hanbury Brown, R. &. Twiss, R. Q. «A test of a new type of stellar interferometer on Sirius«, Nature 178, 1046-1048 (1956).
-El método suponía un gran avance respecto a los interferómetros de Michelson, mayoritariamente empleados hasta entonces; su popularización y extensión fue muy rápida, derivándose también aplicaciones hacia el campo de la óptica cuántica, donde suscitó controversia en el estudio de las estadísticas fotónicas y, especialmente, de algunos tipos de luz no clásica.
-Para una historia del desarrollo de la nueva interferometría de intensidad, y su aplicación a la medida de los diámetros estelares, puede consultarse:
![]() Calvert, Size of stars: https://mysite.du.edu/~jcalvert/astro/starsiz.htm
Calvert, Size of stars: https://mysite.du.edu/~jcalvert/astro/starsiz.htm
Interferómetro estelar de Michelson
![]() Los interferómetros estelares de Michelson miden la coherencia transversal, es decir, constituyen un método para determinar la función de coherencia de primer orden
Los interferómetros estelares de Michelson miden la coherencia transversal, es decir, constituyen un método para determinar la función de coherencia de primer orden :
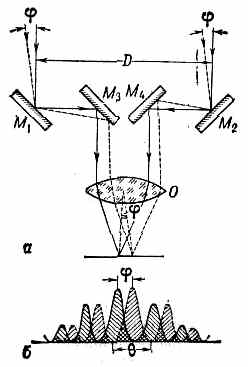
-Un sistema de espejos dirige dos haces paralelos de luz hacia un telescopio, determinándose el diámetro angular a partir de la máxima distancia entre haces a la cual se mantiene la observación de interferencias: si la luz recogida por los espejos es coherente, en el plano focal se forma la correspondiente figura interferencial, pero si hay incoherencia, las intensidades se suman sin interferir.
Se mide el tamaño angular de una estrella mediante la determinación de la coherencia espacial del frente de ondas de la luz filtrada que llega desde ella: para ello se aumenta la distancia
hasta que desaparecen las franjas de interferencia sobre la pantalla, momento en el que se tiene
, donde
es la distancia a la estrella (se supone conocida) y
el diámetro de la estrella:
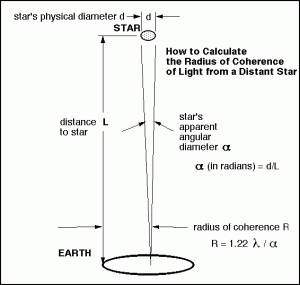
![]() S.C. Zilio, Medidas de diâmetros de estrelas.
S.C. Zilio, Medidas de diâmetros de estrelas.
-Según figuras: la luz procedente de la estrella se refleja en los espejos , produciendo un patrón interferencial sobre la pantalla.
-La intensidad que llega a la pantalla es:
-En el caso de dos ondas planas monocromáticas incidentes la fórmula se convierte en:
donde representa la distancia entre los dos espejos y
es el ángulo entre los dos rayos de luz incidentes.
-De la fórmula se desprende la dificultad de las medidas involucradas: un producto de oscilaciones donde la medida del segundo coseno es requerida para la determinación del ángulo , en un contexto con resultados que son extremadamente sensibles a las variaciones del índice de refracción de la atmósfera interpuesta, que depende de
, de manera que el primer coseno oscila fuerte y rápidamente.
-El interferómetro de Michelson concierne con la coherencia espacial de la luz recogida, que viene determinada por la dispersión en ángulos de la radiación.
![]() En 1920, en Mount Wilson, Los Ángeles, se construyó el primer interferómetro de este tipo, implementado sobre el telescopio que allí había de
En 1920, en Mount Wilson, Los Ángeles, se construyó el primer interferómetro de este tipo, implementado sobre el telescopio que allí había de ; permitía una distancia de
entre los espejos y una resolución angular de unos
radianes para
:

-Para mejorar la resolución angular, se necesita aumentar la separación entre espejos, pero entonces es cada vez más difícil la operación con los espejos que conserve las interferencias.
-El interferómetro estelar de Michelson logró determinar los diámetros estelares de numerosas estrellas, como Betelgeuse, en la constelación de Orión, destacando su papel en el descubrimiento de gigantes rojas.
![]() Javier F.G.: Betelgeuse y el interferómetro estelar de Michelson
Javier F.G.: Betelgeuse y el interferómetro estelar de Michelson
![]() La determinación de la función de coherencia de primer orden informa sobre la coherencia de la luz, y sobre su distribución espectral, pero no proporciona información sobre la correspondiente estadística fotónica.
La determinación de la función de coherencia de primer orden informa sobre la coherencia de la luz, y sobre su distribución espectral, pero no proporciona información sobre la correspondiente estadística fotónica.
Interferómetro estelar HBT
![]() Hanbury-Brown y Twiss propusieron en 1954-56 un nuevo dispositivo experimental para solventar las dificultades del interferómetro estelar de Michelson, cuyo fundamento teórico puede resumirse: en vez de medir la función de coherencia de primer orden,
Hanbury-Brown y Twiss propusieron en 1954-56 un nuevo dispositivo experimental para solventar las dificultades del interferómetro estelar de Michelson, cuyo fundamento teórico puede resumirse: en vez de medir la función de coherencia de primer orden, , determinar la de segundo orden,
,
-Es decir, en vez de involucrar la correlación entre las intensidades de los campos , pasar a considerar las correlaciones entre las intensidades
, salvando así las dificultades que involucraba la formación de la figura interferencial que requería el diseño de Michelson.
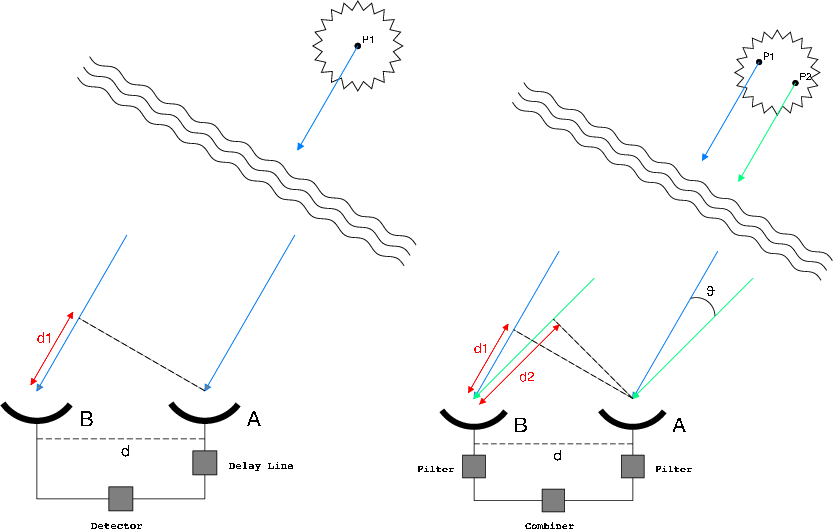
-Para ello propusieron el siguiente esquema básico:
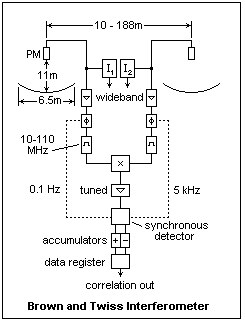
![]() Two aerials, A and B, feed two independent receivers tuned to the same frequency with identical bandpass characteristics. The output of each receiver is rectified in a squarelaw detector and is fed to a lowfrequency band-pass filter. The outputs of these filters are combined in a correlator the output is passed, via an integrating circuit of bandwidth to a pen recording the time-dependent signal (cf. Hanbury Brown y Twiss, op. cit.).
Two aerials, A and B, feed two independent receivers tuned to the same frequency with identical bandpass characteristics. The output of each receiver is rectified in a squarelaw detector and is fed to a lowfrequency band-pass filter. The outputs of these filters are combined in a correlator the output is passed, via an integrating circuit of bandwidth to a pen recording the time-dependent signal (cf. Hanbury Brown y Twiss, op. cit.).
-Dos fotocátodos se sitúan en dos puntos espaciales diferentes, a una distancia dada , y detectan sendas intensidades de luz
, que son ampliadas e integradas en un correlacionador, que proporciona una señal de salida:
-En el caso de dos ondas planas monocromáticas:
expresión que no presenta las dificultades de determinación señaladas antes en la análoga para interferometría de Michelson.
-Cuando la separación entre los fotocátodos es pequeña, los dos detectores recogen luz procedente de una misma área de la fuente, de forma que
; pero cuando se separan, aumentando
, los dos detectores diferencian entre la luz que llega de cada posición,
, y el promedio temporal
cambia.
-Pese a sus ventajas, el procedimiento de interferometría estelar de intensidad también tiene sus limitaciones: principalmente que requiere luz caótica y, en segundo lugar, la rápida disminución de las fluctuaciones en la correlación al disminuir la temperatura.
![]() Tras realizar diversos experimentos en su laboratorio durante 1955-56, que les convencieron de que el nuevo método funcionaba, aplicándolo a la determinación del diámetro de Sirius, Hanbury Brown y Twiss se trasladaron a Australia, donde se construyó un interferómetro (Narrabri, figura de portada) que podía alcanzar valores
Tras realizar diversos experimentos en su laboratorio durante 1955-56, que les convencieron de que el nuevo método funcionaba, aplicándolo a la determinación del diámetro de Sirius, Hanbury Brown y Twiss se trasladaron a Australia, donde se construyó un interferómetro (Narrabri, figura de portada) que podía alcanzar valores de hasta
.
Experimentos de Hanbury Brown-Twiss
![]() En el desarrollo de su proyecto, Hanbury-Brown y Twiss realizaron en 1955 el siguiente experimento, con el objetivo de probar que el método propuesto era aplicable a la luz visible y las medidas de las correlaciones entre las salidas de dos fotomultiplicadores realizables, algo que no estaba claro porque involucraba una etapa de procesado electrónico en la que podía alterarse la función de coherencia (este problema no se presentaba en la banda de radiofrecuencias, ya que la escala temporal de fluctuaciones es mucho más larga en ella):
En el desarrollo de su proyecto, Hanbury-Brown y Twiss realizaron en 1955 el siguiente experimento, con el objetivo de probar que el método propuesto era aplicable a la luz visible y las medidas de las correlaciones entre las salidas de dos fotomultiplicadores realizables, algo que no estaba claro porque involucraba una etapa de procesado electrónico en la que podía alterarse la función de coherencia (este problema no se presentaba en la banda de radiofrecuencias, ya que la escala temporal de fluctuaciones es mucho más larga en ella):
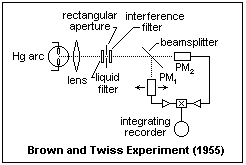
-Usaron como fuente de luz una lámpara de Hg que, tras ser colimada, dotándola de una extensión espacial dada, era dividida (espejo semirreflector o divisor de haz) y llevada a detección sobre dos fotomultiplicadores situados a la misma distancia de la fuente, uno de los cuales podía desplazarse transversalmente; para poder considerar vectores número de ondas bien definidos, ambos cátodos fueron dotados de aperturas que los convertían en aproximadamente puntuales.
-Las dos fotocorrientes generadas, e
, eran llevadas a unas etapas AC amplificadoras, que daban salidas proporcionales a las respectivas fluctuaciones
; a una de ellas se le genera un retardo
; tras ello, las dos confluyen en una unidad integradora que las multiplica e integra sobre un largo período de tiempo, de manera que la señal final es proporcional a
.
–El montaje mide la razón de coincidencia retardada: cuando uno de los detectores registra una cuenta en el tiempo y el otro en el instante
, de modo que cuando el tiempo de retardo
es menor que el tiempo de coherencia,
, se puede obtener información sobre la estadística fotónica de la luz incidente sobre el correspondiente divisor de haz en el montaje.
-Realizaron una serie de medidas, integrando la salida sobre períodos de 90 minutos, de un lado con los detectores superpuestos, de otro con los detectores separados una distancia de orden varias veces su propia anchura. Además, no medían directamente la función de coherencia, sino que tenían que sustraer el fondo:
![]() Hanbury Brown, R. &. Twiss, R. Q. Correlations between photons in two coherent beams of light, Nature 177 (1956) 27-29.
Hanbury Brown, R. &. Twiss, R. Q. Correlations between photons in two coherent beams of light, Nature 177 (1956) 27-29.
![]() Hanbury Brown, R. &. Twiss, R. Q. Proc. Roy. Soc. A242 (1957) 300; A243 (1958) 291.
Hanbury Brown, R. &. Twiss, R. Q. Proc. Roy. Soc. A242 (1957) 300; A243 (1958) 291.
![]() S. Rath, The Hanbury-Brown Twiss and related experiments, Table I.
S. Rath, The Hanbury-Brown Twiss and related experiments, Table I.
![]() Kis Zsolt, Contribution of the Hanbury Brown & Twiss experiment to the development of quantum optics.
Kis Zsolt, Contribution of the Hanbury Brown & Twiss experiment to the development of quantum optics.
-La tabla siguiente resume los resultados que encontraron (los números representan la correlación vía el cociente entre la desviación cuadrática media de la señal y el ruido):
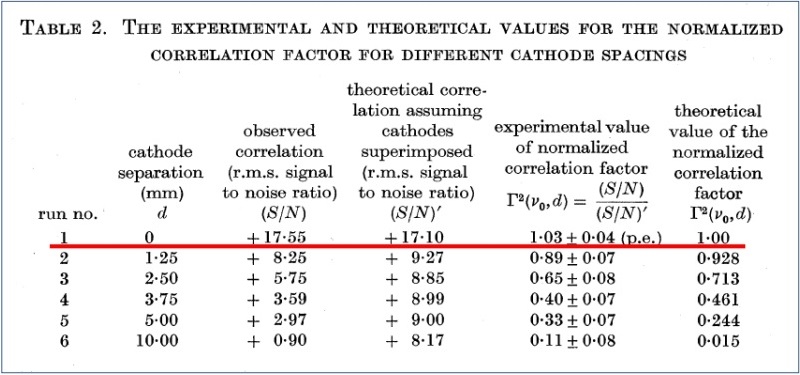
-Aunque aparecían pequeñas discrepancias respecto a las predicciones teóricas, el resultado concuerda perfectamente con la predicción de una teoría clásica de la luz, confirmando la coherencia reforzada (bunching) para pequeñas separaciones espaciales y su pérdida al aumentar dicha separación.
-Los autores concluían:
![]() This experiment shows beyond question that the photons in two coherent beams of light are correlated, and that this correlation is preserved in the process of photoelectric emission. Furthermore, the quantitative results are in fair agreement with those predicted by classical electromagnetic wave theory and the correspondence principle.
This experiment shows beyond question that the photons in two coherent beams of light are correlated, and that this correlation is preserved in the process of photoelectric emission. Furthermore, the quantitative results are in fair agreement with those predicted by classical electromagnetic wave theory and the correspondence principle.
-HBT interpretaron sus resultados como un efecto de agrupamiento fotónico (photon-bunching), efecto HBT, que hicieron compatible con el carácter fotónico de la luz invocando el carácter bosónico del fotón, que haría plausible el aumento de la probabilidad de la llegada simultánea de fotones a los detectores. Posteriormente, Glauber vendría a establecer que la luz del arco de mercurio no es coherente, de modo que las fluctuaciones de intensidad clásicas en la luz termal emitida por la lámpara de Hg son suficientes para una explicación del fenómeno, sin necesidad de invocar la estadística bosónica. Cuando se emplea luz perfectamente coherente, un láser, el efecto HBT no aparece, y la llegada de los fotones no muestra agrupamiento, siendo descrita como un proceso aleatorio de tipo poissoniano puro.
![]() Es interesante señalar que, aunque este experimento se considera hoy una piedra angular para el posterior desarrollo de la óptica cuántica, al mostrar por primera vez los efectos de interferencia en la función de correlación de segundo orden, que involucra las intensidades y, por tanto, muestra una correlación fotón-fotón, en su momento levantó una controversia: algunos autores lo tomaron, erróneamente, como un resultado en contra de la hipótesis fotónica, que parecía inconsistente con la correlación observada.
Es interesante señalar que, aunque este experimento se considera hoy una piedra angular para el posterior desarrollo de la óptica cuántica, al mostrar por primera vez los efectos de interferencia en la función de correlación de segundo orden, que involucra las intensidades y, por tanto, muestra una correlación fotón-fotón, en su momento levantó una controversia: algunos autores lo tomaron, erróneamente, como un resultado en contra de la hipótesis fotónica, que parecía inconsistente con la correlación observada.
-Y es que los resultados, perfectamente explicables en el marco de la teoría de la radiación clásica, ondulatoria, aparentemente presentaban dificultades de comprensión en un marco corpuscular: dada la observada correlación, ¿cómo entenderla para fotones procedentes de distintos y lejanos átomos en una estrella y medidos en dos detectores separados?
-Sobre esta cuestión histórica puede consultarse:
![]() Presentación de I. Lila Silva, «The Controversy on Photons and the Hanbury Brown & Twiss Experiment«, HQ-3 Conference on the History of Quantum Physics, Berlin, 2010, donde recogen la siguiente afirmación de Hanbury Brown en un análisis posterior de la situación, ya en 1991:
Presentación de I. Lila Silva, «The Controversy on Photons and the Hanbury Brown & Twiss Experiment«, HQ-3 Conference on the History of Quantum Physics, Berlin, 2010, donde recogen la siguiente afirmación de Hanbury Brown en un análisis posterior de la situación, ya en 1991:
![]() To me the most interesting thing about all this fuss was that so many physicists had failed to grasp how profoundly mysterious light really is, and were reluctant to accept the practical consequences of the fact that modern physics doesn’t claim to tell us what things are like ‘in themselves’ but only how they ‘behave’. […] If our system was really going to work, one would have to imagine photons hanging about waiting for each other in space!
To me the most interesting thing about all this fuss was that so many physicists had failed to grasp how profoundly mysterious light really is, and were reluctant to accept the practical consequences of the fact that modern physics doesn’t claim to tell us what things are like ‘in themselves’ but only how they ‘behave’. […] If our system was really going to work, one would have to imagine photons hanging about waiting for each other in space!
![]() Presentación, U. Freiburg, Oberholzer:
Presentación, U. Freiburg, Oberholzer:
http://www.capri-school.eu/capri06/lectures/Oberholzer_2.pdf
![]() El caso es que sus experimentos no revelaban ningún efecto puramente cuántico, ya que su dispositivo no usaba detectores de la eficiencia necesaria (no disponibles en la época) y, además, empleaban «luz clásica».
El caso es que sus experimentos no revelaban ningún efecto puramente cuántico, ya que su dispositivo no usaba detectores de la eficiencia necesaria (no disponibles en la época) y, además, empleaban «luz clásica».
![]() Observaron un efecto real de correlación en la llegada de los fotones con una luz que no era monofotónica, ni tampoco completamente coherente: hoy sabemos que el arco de Hg no emite luz coherente, un tipo de luz del que no se dispondría hasta la década de los 60, con el desarrollo de las fuentes de luz láser, cuyo tratamiento téorico riguroso sería posible gracias al formalismo desarrollado por Glauber.
Observaron un efecto real de correlación en la llegada de los fotones con una luz que no era monofotónica, ni tampoco completamente coherente: hoy sabemos que el arco de Hg no emite luz coherente, un tipo de luz del que no se dispondría hasta la década de los 60, con el desarrollo de las fuentes de luz láser, cuyo tratamiento téorico riguroso sería posible gracias al formalismo desarrollado por Glauber.
![]() P. Goodman, W. S. Langer and S. P. Brumby, The Twiss-Hanbury Brown Controversy : A 40-Years Perspective.
P. Goodman, W. S. Langer and S. P. Brumby, The Twiss-Hanbury Brown Controversy : A 40-Years Perspective.
Teoría clásica
![]() B. Bai, Y. Zhou, R. Liu, H. Zheng, Y. Wang, F. Li & Z. Xu, Hanbury Brown-Twiss effect without two-photon interference in photon counting regime, Scientific Reports 7 (2017) 2145; https://doi.org/10.1038/s41598-017-02408-6.
B. Bai, Y. Zhou, R. Liu, H. Zheng, Y. Wang, F. Li & Z. Xu, Hanbury Brown-Twiss effect without two-photon interference in photon counting regime, Scientific Reports 7 (2017) 2145; https://doi.org/10.1038/s41598-017-02408-6.
![]() I. Silva and O. Freire Jr, The Concept of the Photon in Question: The Controversy Surrounding the HBT Effect circa 1956–1958, Historical Studies in the Natural Sciences 43, 4 (2013) 453-491.
I. Silva and O. Freire Jr, The Concept of the Photon in Question: The Controversy Surrounding the HBT Effect circa 1956–1958, Historical Studies in the Natural Sciences 43, 4 (2013) 453-491.
![]() [FOX-06] Fox, M.; Quantum Optic. An introduction. Oxford Univ. Press; Oxford, 2006, pp. 108-110.
[FOX-06] Fox, M.; Quantum Optic. An introduction. Oxford Univ. Press; Oxford, 2006, pp. 108-110.
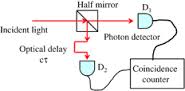
![]() La luz emitida por una lámpara de Hg es una luz parcialmente coherente o caótica (luz super-poissoniana), ya que se origina a partir de muchos átomos, lo que comporta fluctuaciones en la intensidad emitida cuya escala temporal es del orden del parámetro de coherencia
La luz emitida por una lámpara de Hg es una luz parcialmente coherente o caótica (luz super-poissoniana), ya que se origina a partir de muchos átomos, lo que comporta fluctuaciones en la intensidad emitida cuya escala temporal es del orden del parámetro de coherencia . Estas fluctuaciones se deben tanto a las correspondientes al número de átomos que emiten en un instante dado como a las discontinuidades en la fase con que emiten los distintos átomos, radicadas en la aleatoriedad fundamental de los procesos a nivel microscópico.
-Las fluctuaciones en la intensidad se relacionan con la coherencia del haz: si las luces que caen sobre cada detector son coherentes, sus fluctuaciones están correlacionadas, y midiendo esta correlación, puede derivarse la coherencia, sin necesidad de obtener una figura interferencial.
-En el experimento HBT:
- Cuando la distancia
se anula, solapamiento espacial de los dos detectores, y supuesto que el divisor de haz es perfectamente simétrico (50:50), las dos intensidades resultan iguales, con expresión en términos de la corriente total
que llega al divisor de haz:
siendo la salida final:
.
- Para un retardo
, la salida es:
ya que, si bien, en cambio
, debido a las fluctuaciones en intensidad inherentes a una luz caótica como la que emite la lámpara de descarga.
- Si
, las fluctuaciones de intensidad en los dos detectores no estarán correlacionadas en absoluto, de forma que
cambiará aleatoriamente y su promedio temporal se anulará:
- Por tanto, midiendo la salida como función de
, puede determinarse
.
![]() HBT fijaron
HBT fijaron y variaron
: al aumentarlo, la coherencia espacial entre la luz sobre los dos detectores disminuye, de forma que la correlación entre las dos
disminuye, hasta anularse si
es suficientemente grande.
Interferómetros HBT o de intensidad
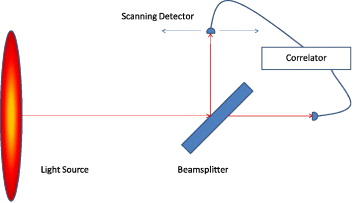
![]() En definitiva, en un interferómetro de Hanbury-Brown Twiss, cuyo esquema general es:
En definitiva, en un interferómetro de Hanbury-Brown Twiss, cuyo esquema general es:
se puede determinar la función de coherencia cuántica de segundo orden,
representando la probabilidad condicional de que se detecte, en una posición dada, un fotón en y también otro en
, esto es, con un retardo
.
![]() [FOX-06] Fox, M.; Quantum Optic. An introduction. Oxford Univ. Press; Oxford, 2006, pp. 113-115, 160-163.
[FOX-06] Fox, M.; Quantum Optic. An introduction. Oxford Univ. Press; Oxford, 2006, pp. 113-115, 160-163.
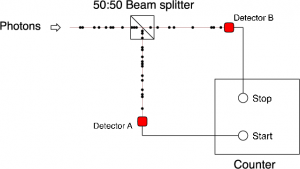
![]() El contador va registrando el tiempo entre las señales de cada detector, al mismo tiempo que el número de detecciones o pulsos en cada uno, de forma que se registran coincidencias del tipo: un fotón es detectado en
El contador va registrando el tiempo entre las señales de cada detector, al mismo tiempo que el número de detecciones o pulsos en cada uno, de forma que se registran coincidencias del tipo: un fotón es detectado en en
, y otro en
en
, donde
es la duración de cada pulso.
-Tras muchas repeticiones, y normalizando por el número total de registros de cada detector, lo que se obtiene es la función de coherencia (semi-clásica) de segundo orden, la cual, puesto que el número de cuentas registrado en cada detector es proporcional a la intensidad, puede expresarse también como:
donde es el número de cuentas en cada detector,
en el instante
; la función indica la probabilidad simultánea de detectar un fotón en
en
, y otro después, en
, en
. Es decir: la función de coherencia
es proporcional a la probabilidad condicional de detectar un segundo fotón en
, una vez que hubo una detección de uno en un tiempo anterior
, aceptada la interpretación cuántica corpuscular.
![]() El efecto Hanbury Brown-Twiss, o efecto de agrupamiento fotónico (photon bunching), es pues perfectamente explicable en términos de una teoría ondulatoria de la luz, pero en los años 50 resultó difícil de entender para algunos científicos desde el aspecto corpuscular o fotónico: si la fuente de luz emite fotones al azar, ¿cómo es que llegan al detector en una forma correlacionada (agrupada)?
El efecto Hanbury Brown-Twiss, o efecto de agrupamiento fotónico (photon bunching), es pues perfectamente explicable en términos de una teoría ondulatoria de la luz, pero en los años 50 resultó difícil de entender para algunos científicos desde el aspecto corpuscular o fotónico: si la fuente de luz emite fotones al azar, ¿cómo es que llegan al detector en una forma correlacionada (agrupada)?
![]() La respuesta la proporciona el modelo de luz agrupada: si se considera que los fotones llegan agrupados, en cada paquete la mitad de ellos se dirigirá hacia el detector
La respuesta la proporciona el modelo de luz agrupada: si se considera que los fotones llegan agrupados, en cada paquete la mitad de ellos se dirigirá hacia el detector y la otra mitad hacia el
, de forma que se tendrá una alta probabilidad de que se produzcan detecciones en coincidencia y, por tanto, un alto número de sucesos cuando
. Pero, al aumentar
, el número de eventos registrados caerá.
-En cualquier caso, la luz agrupada se corresponde con valores de compatibles con la teoría clásica.
Donde la teoría clásica fracasa es en la explicación de los resultados que se obtienen en un interferómetro HBT empleando luz antiagrupada, en la que los fotones van llegando con intervalo de separación temporal fijo y lo que se registra es la ausencia de eventos para
, con un cero en el origen (idealmente, en la práctica una acusada disminución) en la función
.
![]() La función de coherencia cuántica de segundo orden tiene la expresión:
La función de coherencia cuántica de segundo orden tiene la expresión:
donde es el operador número de fotones, detectados en
, y lo mismo para
.
-Es decir, mientras que la función clásica se define en términos de las fluctuaciones de intensidad de la luz incidente, la función cuántica se define en términos de coincidencias de eventos de detección fotónica.
-Para se obtiene:
-El estado de entrada, ya que el segundo canal de entrada está vacío, es (canales de entrada incidentevacío ; canales de salida
):
-La transformación que realiza el divisor de haz:
,
un resultado que para luz incidente en estados número, ,
, proporciona:
para una fuente de luz monofotónica, es decir, que emite luz en estados con
: un resultado no clásico.
El resultado no clásico
sólo es posible para estados cuánticos de la luz que exhiben el fenómeno de antiagrupamiento.
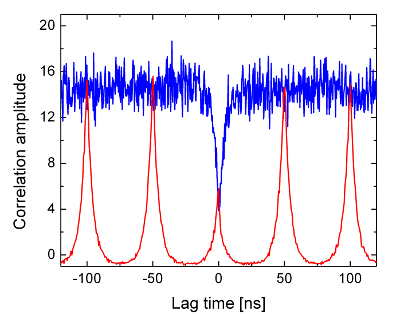
-En la práctica, aunque se obtiene claramente la disminución del valor de , los valores medidos son pequeños pero no nulos, tanto por la dificultad de trabajar con auténtica luz monofotónica como por la limitada eficiencia de los detectores, que tienen una respuesta temporal finita.
![]() En los dos casos de resultados HBT expuestos, para luz agrupada (bunched photons, una luz clásica) y luz antiagrupada (antibunched photons, una luz no clásica) es crucial que se emplee luz caótica: no se observa correlación alguna de intensidades si se emplea luz perfectamente coherente (luz clásica) como la láser, por ejemplo, ya que no se produciría el efecto requerido de o bien luz agrupada, photon bunching, o bien luz antiagrupada (caso de fuentes de pulsos monofotónicos). Y ello porque la luz perfectamente coherente presenta estadística poissoniana.
En los dos casos de resultados HBT expuestos, para luz agrupada (bunched photons, una luz clásica) y luz antiagrupada (antibunched photons, una luz no clásica) es crucial que se emplee luz caótica: no se observa correlación alguna de intensidades si se emplea luz perfectamente coherente (luz clásica) como la láser, por ejemplo, ya que no se produciría el efecto requerido de o bien luz agrupada, photon bunching, o bien luz antiagrupada (caso de fuentes de pulsos monofotónicos). Y ello porque la luz perfectamente coherente presenta estadística poissoniana.
La explicación teórica de la diferencia de comportamiento entre la luz perfectamente coherente (como la láser) y la luz caótica (como la termal) fue desarrollada por Glauber, quien recibiría por ello el Premio Nobel en 2005, «por su contribución a la teoría de la coherencia óptica cuántica».
Interferometría HBT con partículas materiales y otras aplicaciones
![]() HBT Interferometry with Interacting photons
HBT Interferometry with Interacting photons
![]() Presentación, U. Freiburg, Oberholzer: http://www.capri-school.eu/capri06/lectures/Oberholzer_2.pdf
Presentación, U. Freiburg, Oberholzer: http://www.capri-school.eu/capri06/lectures/Oberholzer_2.pdf
![]() HBT para electrones libres:
HBT para electrones libres:
http://www.nature.com/nature/journal/v418/n6896/full/nature00911.html
![]() HBT con átomos ultra-fríos:
HBT con átomos ultra-fríos:
http://scienceblogs.com/principles/2010/08/24/bunches-and-antibunches-of-ato/
![]() Sobre la gran dificultad experimental de realizar buenas medidas de la función de coherencia de segundo orden:
Sobre la gran dificultad experimental de realizar buenas medidas de la función de coherencia de segundo orden:
http://www.opticsinfobase.org/oe/fulltext.cfm?uri=oe-17-17-15087&id=184546
Bibliografía
[FOX-06] Fox, M.; Quantum Optic. An introduction. Oxford Univ. Press; Oxford, 2006.
![]() B. Bai, Y. Zhou, R. Liu, H. Zheng, Y. Wang, F. Li & Z. Xu, Hanbury Brown-Twiss effect without two-photon interference in photon counting regime, Scientific Reports 7 (2017) 2145; https://doi.org/10.1038/s41598-017-02408-6.
B. Bai, Y. Zhou, R. Liu, H. Zheng, Y. Wang, F. Li & Z. Xu, Hanbury Brown-Twiss effect without two-photon interference in photon counting regime, Scientific Reports 7 (2017) 2145; https://doi.org/10.1038/s41598-017-02408-6.
![]() U. Berlín, Lehre: Coherence properties of the electromagnetic field
U. Berlín, Lehre: Coherence properties of the electromagnetic field
![]() S. Rath: The Hanbury Brown-Twiss and related Experiments
S. Rath: The Hanbury Brown-Twiss and related Experiments
![]() Y. Lahini, Y. Bromberg, E. Small and Y. Silberberg, Hanbury Brown and Twiss Interferometry with Interacting Photons.
Y. Lahini, Y. Bromberg, E. Small and Y. Silberberg, Hanbury Brown and Twiss Interferometry with Interacting Photons.
![]() K. Guzek and A. Howard; Single Emitters and the Experimental Demonstration of Photon Antibunching.
K. Guzek and A. Howard; Single Emitters and the Experimental Demonstration of Photon Antibunching.
![]() Presentación, Oberholzer:
Presentación, Oberholzer:
http://www.capri-school.eu/capri06/lectures/Oberholzer_2.pdf
![]() Presentación de L. Silva: http://quantum-history.mpiwg-berlin.mpg.de/news/workshops/hq3/hq3_talks/23_silva.pdf
Presentación de L. Silva: http://quantum-history.mpiwg-berlin.mpg.de/news/workshops/hq3/hq3_talks/23_silva.pdf
![]() G. Baym, The physics of Hanbury Brown–Twiss intensity interferometry: from stars to nuclear collisions.
G. Baym, The physics of Hanbury Brown–Twiss intensity interferometry: from stars to nuclear collisions.
![]() B. Silva et al., The colored Hanbury Brown–Twiss effect.
B. Silva et al., The colored Hanbury Brown–Twiss effect.
![]() C. Foellmi, Intensity interferometry and the second-order correlation function g $^{\sf (2)}$ in astrophysics; AA, vol. 507, 3, p. 1719 – 1727; DOI: https://doi.org/10.1051/0004-6361/200911739.
C. Foellmi, Intensity interferometry and the second-order correlation function g $^{\sf (2)}$ in astrophysics; AA, vol. 507, 3, p. 1719 – 1727; DOI: https://doi.org/10.1051/0004-6361/200911739.
-En la Wikipedia: https://es.m.wikipedia.org/wiki/Efecto_Hanbury_Brown_y_Twiss
Dejar una contestacion