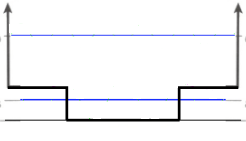
Pozo cuadrado finito en seno pozo infinito
- Función potencial
:
donde
es un número real positivo, con dimensiones de energía.
-Se trata de una función con discontinuidades de segunda especie en los puntos, puntos en los que se sitúan sendas barreras impenetrables de potencial; por lo tanto, en ellos se debe imponer la condición de frontera de anulación de la función de onda
: se produce el confinamiento o ligadura de la partícula en el interior del intervalo
de la recta real, de longitud
; la derivada primera de la función de onda presentará discontinuidades en ambos extremos. Por otra parte, el potencial presenta discontinuidades de primera especie en los puntos
, puntos en los que habrá que proceder al empalme o conexión de las respectivas soluciones en las zonas I y II que garantice la continuidad de la función de onda y su primera derivada.
- Problema de autovalores de energía:
,
y buscamos solucionesque sean funciones continuas y con derivada primera
también continua allí donde
es finito: en el intervalo
; las funciones
tendrán sendos nodos en los puntos extremos
:
(donde
presentará una discontinuidad de primera especie).
- La solución general de una EDO
,
donde,
, tiene la expresión:
-Signo (-) :
conescalares arbitrarios.
-Signo (+) :
conescalares arbitrarios.
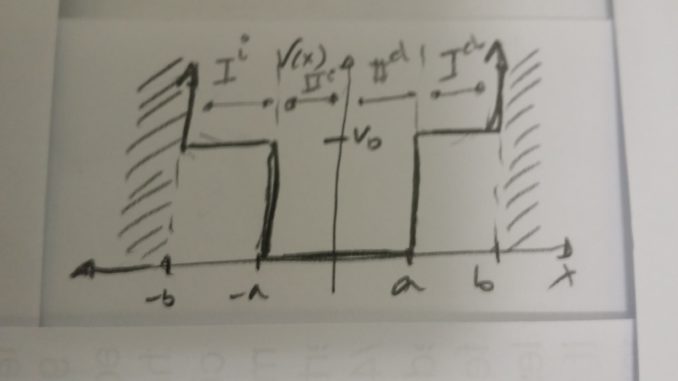
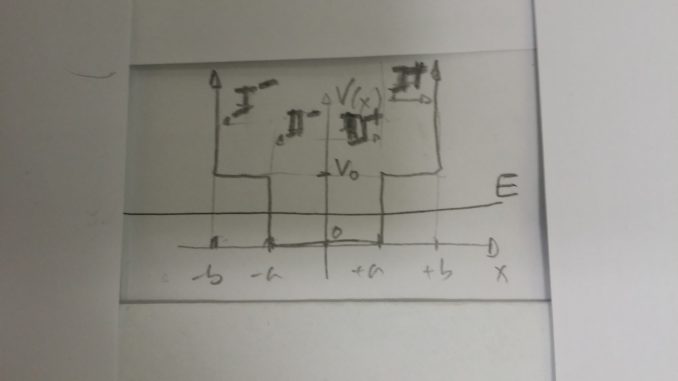
- En las dos regiones espaciales consideradas, I:
y II:
, las respectivas formas de la EDO planteada son:
Zona II ::
Zona I ::
- Puesto que el potencial es simétrico en torno al origen, sabemos de antemano que los autoestados van a tener paridad definida; por ello, iremos incorporando la paridad de partida, limitándonos además a resolver en la parte positiva del eje real.
:
- Forma A de resolución:
- -Zona I:
:
cony
escalares arbitrarios.
-Zona II::
cony
escalares arbitrarios.
-Zona:
.
- Soluciones pares
para
:
- Por ser la función par, ha de tenerse
.
- La función de onda par tendrá la expresión general:
- Imponiendo las condiciones para que la solución sea físicamente aceptable:
-Anulaciónen
-Continuidaden
-Continuidaden
-Obsérvese que ha de serno nula en
, ya que, caso contrario, el conjunto de condiciones conduciría a la solución trivial.
- Dividiendo entre sí las anteriores ecuaciones tercera y segunda:
- Por tanto, se obtiene la condición de cuantización de la energía o ecuación cuyas raíces proporcionan los autovalores correspondientes a las autofunciones pares:
-Las raícesde esta ecuación trascendente constituyen los autovalores de la energía
, o puntos espectrales del Hamiltoniano, en el tramo de energía
, correspondientes a las autofunciones pares.
- Resolución gráfica:
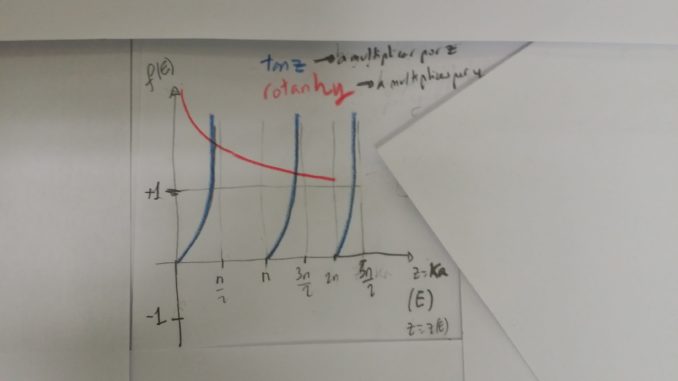
- Expresión de las autofunciones pares
:
donde
;
;
son los distintos autovalores pares, obtenidos a partir de la resolución de la ecuación de autovalores pares;
yes una constante a determinar por normalización de la correspondiente función de onda
.
- Por ser la función par, ha de tenerse
- Soluciones impares
para
:
- Por ser la función impar, ha de tenerse
.
- La función de onda impar tendrá la expresión general:
- Imponiendo las condiciones para que la solución sea físicamente aceptable:
-Anulaciónen
-Continuidaden
-Continuidaden
-Obsérvese que ha de serno nula en
, ya que, caso contrario, el conjunto de condiciones conduciría a la solución trivial.
- Dividiendo entre sí las anteriores ecuaciones tercera y segunda:
- Por tanto, se obtiene la condición de cuantización o ecuación cuyas raíces proporcionan los autovalores correspondientes a las autofunciones impares:
-Las raícesde esta ecuación trascendente constituyen los autovalores de la energía, o puntos espectrales del Hamiltoniano, en el tramo de energía
, correspondientes a las autofunciones impares.
- Resolución gráfica:
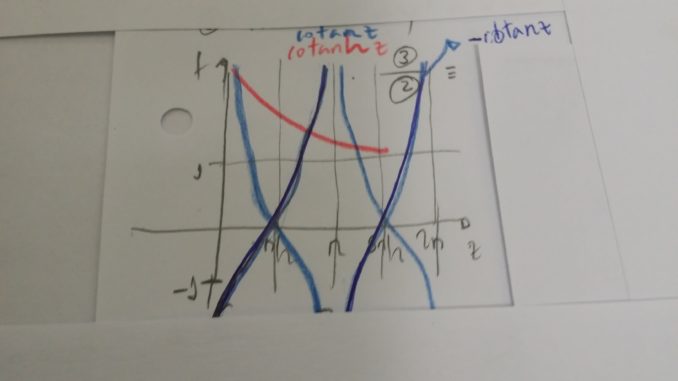
- Expresión de las autofunciones impares
:
donde
;
;
son los distintos autovalores impares, obtenidos a partir de la resolución de la ecuación de autovalores impares;
yes una constante a determinar por normalización de la correspondiente función de onda
.
-Nota: equivalentemente, se puede expresar:
- Por ser la función impar, ha de tenerse
- -Zona I:
- Forma B de resolución:
- En esta segunda forma de resolución, lo que se hace es usar en la zona I para la expresión de la función de onda
una combinación lineal de funciones hiperbólicas:
- -Zona I:
:
con
y
escalares arbitrarios.
-Zona II::
con
y
escalares arbitrarios.
-Zona:
.
- Como ha de tenerse anulación de la función de onda en
, se deriva:
;
renombramos,
eligiendo el nuevo par de constantes arbitrarias, tales que:
y
,
en términos de las cuales la función de onda en la zona I pasa a expresarse como:
-Zona I::
,
cony
escalares arbitrarios.
- Soluciones pares
para
:
- Por ser la función par, ha de tenerse
.
- La función de onda par tendrá la expresión general:
- Imponiendo las condiciones para que la solución sea físicamente aceptable:
-Anulaciónen
-Continuidaden
-Continuidaden
-Obsérvese que ha de serno nula en
, ya que, caso contrario, el conjunto de condiciones conduciría a la solución trivial.
- Dividiendo entre sí las anteriores ecuaciones tercera y segunda, se llega a la misma condición de cuantización para los autovalores de energía correspondientes a las autofunciones pares que se obtuvo antes por el camino A:
.
-Las raícesde esta ecuación trascendente constituyen los autovalores de la energía, o puntos espectrales del Hamiltoniano, en el tramo de energía
, correspondientes a las autofunciones pares.
- Expresión de las autofunciones pares
:
donde
;
;
son los distintos autovalores pares, obtenidos a partir de la resolución de la ecuación de autovalores pares;
yes una constante a determinar por normalización de la correspondiente función de onda
.
- Por ser la función par, ha de tenerse
- Soluciones impares
para
:
- Por ser la función impar, ha de tenerse
.
- La función de onda impar tendrá la expresión general:
- Imponiendo las condiciones para que la solución sea físicamente aceptable:
-Anulaciónen
-Continuidaden
-Continuidaden
-Obsérvese que ha de serno nula en
, ya que, caso contrario, el conjunto de condiciones conduciría a la solución trivial.
- Dividiendo entre sí las anteriores ecuaciones tercera y segunda, se llega a la misma ecuación de autovalores o condición de cuantización para los autovalores de energía correspondientes a las autofunciones impares que se obtuvo antes por el camino A:
-Las raícesde esta ecuación trascendente constituyen los autovalores de la energía, o puntos espectrales del Hamiltoniano, en el tramo de energía
, correspondientes a las autofunciones impares.
- Expresión de las autofunciones impares
:
donde
;
;
son los distintos autovalores pares, obtenidos a partir de la resolución de la ecuación de autovalores impares;
yes una constante a determinar por normalización de la correspondiente función de onda
.
-Nota: equivalentemente, se puede expresar:
- Por ser la función impar, ha de tenerse
- En esta segunda forma de resolución, lo que se hace es usar en la zona I para la expresión de la función de onda
- Forma A de resolución:
:
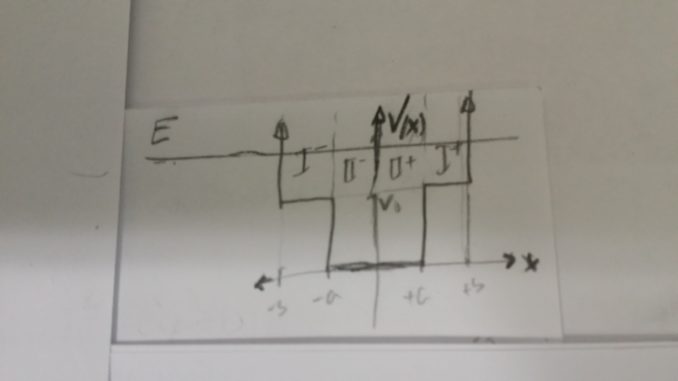
- Forma A de resolución:
- -Zona I:
:
cony
escalares arbitrarios.
-Zona II::
cony
escalares arbitrarios.
-Zona:
.
-De manera que, en este tramo de valores de, la solución es oscilatoria en las dos zonas I y II.
- Soluciones pares
para
:
- Por ser la función par, ha de tenerse
.
- La función de onda par tendrá la expresión general:
- Imponiendo las condiciones para que la solución sea físicamente aceptable:
-Anulaciónen
-Continuidaden
-Continuidaden
-Obsérvese que ha de serno nula en
, ya que, caso contrario, el conjunto de condiciones conduciría a la solución trivial.
- Dividiendo entre sí las anteriores ecuaciones tercera y segunda:
- Por tanto, se obtiene la condición de cuantización de la energía o ecuación de autovalores para las autofunciones pares:
-Las raícesde esta ecuación trascendente constituyen los autovalores de la energía
, o puntos espectrales del Hamiltoniano, en el tramo de energía
, correspondientes a las autofunciones pares.
- Resolución gráfica: como antes.
- Expresión de las autofunciones pares
:
donde
;
;
son los distintos autovalores pares, obtenidos a partir de la resolución de la ecuación de autovalores pares;
yes una constante a determinar por normalización de la correspondiente función de onda
.
- Por ser la función par, ha de tenerse
- Soluciones impares
para
:
- Por ser la función impar, ha de tenerse
.
- La función de onda impar tendrá la expresión general:
- Imponiendo las condiciones para que la solución sea físicamente aceptable:
-Anulaciónen
-Continuidaden
-Continuidaden
-Obsérvese que ha de serno nula en
, ya que, caso contrario, el conjunto de condiciones conduciría a la solución trivial.
- Dividiendo entre sí las anteriores ecuaciones tercera y segunda:
- Por tanto, se obtiene la condición de cuantización o ecuación de autovalores para las autofunciones impares:
-Las raícesde esta ecuación trascendente constituyen los autovalores de la energía, o puntos espectrales del Hamiltoniano, en el tramo de energía
, correspondientes a las autofunciones impares.
- Resolución gráfica: como antes.
- Expresión de las autofunciones impares
:
donde
;
;
son los distintos autovalores impares, obtenidos a partir de la resolución de la ecuación de autovalores impares;
yes una constante a determinar por normalización de la correspondiente función de onda
.
-Nota: equivalentemente, se puede expresar:
- Por ser la función impar, ha de tenerse
- -Zona I:
- Forma B de resolución:
- En esta segunda forma de resolución, lo que se hace es usar en la zona I para la expresión de la función de onda
una expresión trigonométrica:
- -Zona I:
:
cony
escalares arbitrarios.
-Zona II::
cony
escalares arbitrarios.
-Zona:
.
- Como ha de tenerse anulación de la función de onda en
, se deriva:
;
renombramos,
eligiendo el nuevo par de constantes arbitrarias, tales que:
y
,
en términos de las cuales la función de onda en la zona I pasa a expresarse como:
-Zona I::
,
cony
escalares arbitrarios.
- Soluciones pares
para
:
- Por ser la función par, ha de tenerse
.
- La función de onda par tendrá la expresión general:
- Imponiendo las condiciones para que la solución sea físicamente aceptable:
-Anulaciónen
; elegimos
.
-Continuidaden
-Continuidaden
-Obsérvese que ha de serno nula en
, ya que, caso contrario, el conjunto de condiciones conduciría a la solución trivial.
- Dividiendo entre sí las anteriores ecuaciones tercera y segunda, se llega a la misma condición de cuantización para los autovalores de energía correspondientes a las autofunciones pares que se obtuvo antes por el camino A:
.
-Las raícesde esta ecuación trascendente constituyen los autovalores de la energía, o puntos espectrales del Hamiltoniano, en el tramo de energía
, correspondientes a las autofunciones pares.
- Expresión de las autofunciones pares
:
donde
;
;
son los distintos autovalores pares, obtenidos a partir de la resolución de la ecuación de autovalores pares;
yes una constante a determinar por normalización de la correspondiente función de onda
.
- Por ser la función par, ha de tenerse
- Soluciones impares
para
:
- Por ser la función impar, ha de tenerse
.
- La función de onda impar tendrá la expresión general:
- Imponiendo las condiciones para que la solución sea físicamente aceptable:
-Anulaciónen
, elegimos
-Continuidaden
-Continuidaden
-Obsérvese que ha de serno nula en
, ya que, caso contrario, el conjunto de condiciones conduciría a la solución trivial.
- Dividiendo entre sí las anteriores ecuaciones tercera y segunda, se llega a la misma condición de cuantización para los autovalores de energía correspondientes a las autofunciones impares que se obtuvo antes por el camino A:
-Las raícesde esta ecuación trascendente constituyen los autovalores de la energía, o puntos espectrales del Hamiltoniano, en el tramo de energía
, correspondientes a las autofunciones impares.
- Expresión de las autofunciones impares
:
donde
;
;
son los distintos autovalores pares, obtenidos a partir de la resolución de la ecuación de autovalores impares;
yes una constante a determinar por normalización de la correspondiente función de onda
.
-Nota: equivalentemente, se puede expresar:
- Por ser la función impar, ha de tenerse
- En esta segunda forma de resolución, lo que se hace es usar en la zona I para la expresión de la función de onda
- Forma A de resolución:
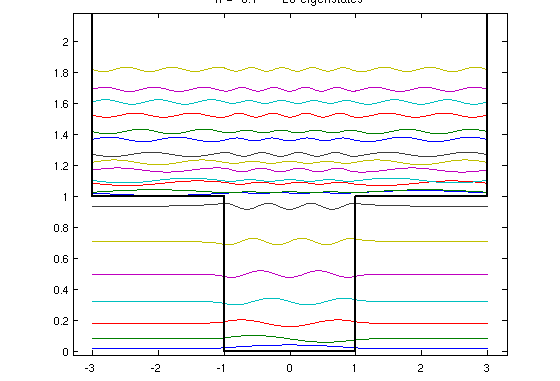
- Las siguiente imágenes nos muestran los correspondiente estados ligados, que satisfacen el teorema de Sturm:
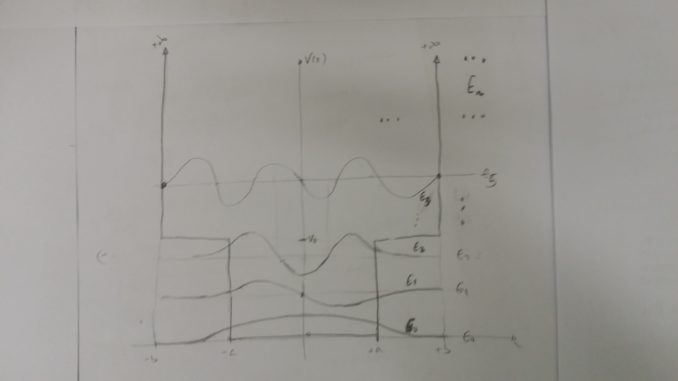
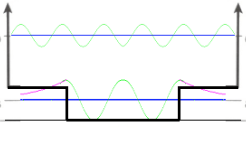
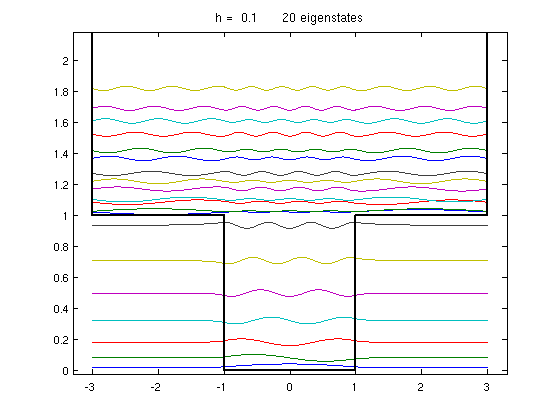
Imagen desde: https://www.mathworks.com/examples/matlab/community/22670-eigenstates-of-the-schroedinger-equation - Nota: los resultados para
se podían haber deducido sin más a partir de los correspondientes a
: hubiera bastado para ello sustituir el parámetro
del cálculo
por
(es decir:
. Por ejemplo, si partimos de la ecuación de los autovalores pares en el tramo de energías
,
,
y realizamos la sustitución indicada, se deriva:
.
- Caso límite: En el límite
, se obtienen los resultados del pozo cuadrado infinito, como es fácil comprobar. En efecto, por ejemplo, el límite
proporciona:
(autovalores de los autoestados pares del pozo infinito).
- En el problema estudiado, Hamiltoniano del pozo cuadrado infinito, o caja de paredes impenetrables, resulta por tanto:
: infinitos estados ligados, sin degeneración; se satisface el teorema de oscilación.
Referencias
[BOH-89] Bohm, D.; «Quantum Theory»; Dover; New York, 1989.
[BRA-00] Bransden, B.H. and Joachain, C.J.; «Quantum Mechanics»; 2nd ed., Pearson; Dorchester, 2000.
[GAL-89] Galindo, A. y Pascual, P.; «Mecánica Cuántica», Eudema, 1989.
[SCH-68] Schiff,L.I.; «Quantum Mechanics»; 3º ed., McGraw; 1968.
Páginas complementarias
http://en.wikipedia.org/wiki/Particle_in_a_box
http://www.uco.es/hbarra/index.php/fc/apuntesfc/334-fc0303
http://eltamiz.com/2008/05/15/cuantica-sin-formulas-el-pozo-de-potencial-infinito/
APPS
http://www.sc.ehu.es/sbweb/fisica/cuantica/pozo/caja.htm
http://www.uco.es/hbarra/index.php/fc/appletsfc/70-pozo-infinito
http://www.uco.es/hbarra/index.php/fc/appletsfc/71-paquete-pozo-infinito
http://www.st-andrews.ac.uk/physics/quvis/embed_item_3.php?anim_id=24&file_sys=index_phys
Probability Density in an Infinite Square Well from the Wolfram Demonstrations Project by Carlos Anton Solanas
Quantum Particles in an Infinite Square Potential Well from the Wolfram Demonstrations Project by Jeff Bryant
-Ejemplos de resolución en MATLAB de distintos potenciales:
https://www.mathworks.com/examples/matlab/community/22670-eigenstates-of-the-schroedinger-equation
Dejar una contestacion