Pruebas experimentales de la contextualidad

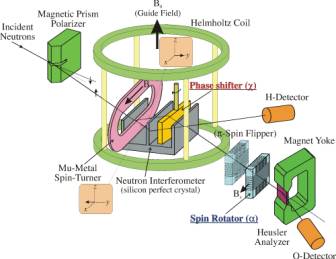
Implementación experimental

 Dos referencias sobre propuestas teóricas de experimentos que pongan a prueba la contextualidad cuántica:

 A. Cabello: Tesis doctoral (1996): Pruebas algebraicas de imposibilidad de variables ocultas en mecánica cuántica, cap. 2.3.6, pp. 47-51.

-Plantea cómo acometer un test experimental del teorema BKS (obviamente no del teorema en sí, que no es sino un resultado matemáticamente indiscutible que muestra la inconsistencia entre la Mecánica Cuántica y cualquier teoría de VO no-contextuales), enfrentando las predicciones sobre un sistema de la mecánica cuántica (teoría con variables contextuales) con las más sencillas que corresponderían a una teoría de VO no-contextuales (las que haga una teoría que suponga definidos a priori el menor número de observables, cf. nota 3 en p. 48). Para permitir una prueba experimental, se acomete una demostración probabilística del teorema BKS.

 Si se compara con los tests experimentales sobre realismo local, la diferencia esencial es que mientras que la violación de una desigualdad de Bell requiere estados entrelazados, en cambio:

 La contextualidad puede ser probada sobre cualquier estado cuántico, no necesariamente entrelazado.

A. Cabello, «Experimentally State-independent Quantum Contextuality», Physical Review Letters 101 (2008) 210401.

Se realizan propuestas de desigualdades derivadas invocando sólo la contextualidad (como sucede con las demostraciones BKS) y que, por lo tanto, se habrían de violar sobre cualquier estado (además de ser contrastables experimentalmente: un paralelismo evidente con las desigualdades de Bell para el realismo local).

-Pero, en la práctica, usar estados entrelazados también permitiría realizar comprobaciones experimentales involucrando menos observables (véase G. García Alcaine, Enredo cuántico, pp. 17ss.).

Otra diferencia esencial es que, puesto que para probar la no contextualidad cuántica no se requiere entrelazamiento, puede también probarse con sistemas sin partes:

 La contextualidad puede ser probada sobre sistemas no compuestos, sin partes:

A. Cabello, «Correlations without parts», Nature 474 (2011) 456–458 ; divulgado en el blog de Francisco R. Villatoro.

Realizaciones experimentales publicadas (selección):

 C. Saulder: Contextuality and the Kochen-Specker Theorem, pp. 11-16.

-El segundo experimento que cita:

 Y. Hasegawa, R. Loidl, G. Badurek, M. Baron and H. Rauch, Nature 425 (2003) 45-48; Violation of a Bell-like inequality in neutron optical experiments: quantum contextuality; Journal of Optics B: Quantum and Semiclassical Optics 6 (2004).

H. Bartosik, J. Klepp, C. Schmitzer, S. Sponar, A. Cabello, H. Rauch and Y. Hasegawa, «Violation of a bell-like inequality in single-neutron interferometer experiments: Quantum contextuality», Journal of Modern Optics 51, 6-7(2004); DOI: 10.1080/09500340408233610.

 Otros experimentos:

 G. Kirchmair, F. Zähringer, R. Gerritsma, M. Kleinmann, O. Gühne, A. Cabello, R. Blatt & C. F. Roos, State-independent experimental test of quantum contextuality, Nature 460 (2009) 494-497; https://arxiv.org/pdf/0904.1655.pdf.

Y. Hasegawa, K. Durstberger-Rennhofer, S. Sponar and H. Rauch, «Kochen–Specker theorem studied with neutron interferometer»; Nucl. Instrumental Methods Phys Res A. 2011 Apr 1; 634(1): S21–S24; DOI: 10.1016/j.nima.2010.06.234.

 C. Zu, Y.-X. Wang, D.-L. Deng, X.-Y. Chang, K. Liu, P.-Y. Hou, H.-X. Yang, and L.-M. Duan, «State-Independent Experimental Test of Quantum Contextuality in an Indivisible System», Phys. Rev. Lett. 109 (2012) 150401.

Pueden verse también los enlaces:

– Para las mediciones cuánticas el sentido común no es suficiente

– Mediciones cuánticas: el sentido común no es suficiente

– Mecánica cuántica: contexto y realidad

 Experimentos sobre contextualidad con qutrits (sistemas no compuestos de tres estados):

-Una demostración experimental de las violación de las desigualdades de Kochen y Specker para un único sistema cuántico, un fotón que puede viajar a lo largo de tres caminos posibles donde se realizan diferentes medidas cuyos resultados deben ser compatibles entre sí:
R. Lapkiewicz et al., «Experimental non-classicality of an indivisible quantum system», Nature 474 (2011) 490–493 , doi: 10.1038/nature10119.

 X. Zhang, M. Um, J. Zhang, S. An, Y. Wang, D.-l. Deng, C. Shen, L.-M. Duan and K. Kim, State-Independent Experimental Test of Quantum Contextuality with a Single Trapped Ion, Phys. Rev. Lett. 110 (2013) 070401.

Otras informaciones:

A. Cabello, «Correlations without parts», Nature 474 (2011) 456-458.

Breno Marques et al., Experimental Observation of Hardy-Like Quantum Contextuality, Phys. Rev. Lett. 113 (2014) 250403, doi: 10.1103/PhysRevLett.113.250403, arXiv:1408.6763.

Entrada del blog Naukas sobre contextualidad

Charla sobre «Contextualidad», por A. Cabello en Buenos Aires, 2015, en Youtube.

De una entrevista a A. Cabello en 2011 (y en el blog de Joanen Cunyat):

Pregunta: En el experimento que has realizado en Estocolmo, habéis encontrado que el comportamiento de los fotones, tomados de uno en uno, no se puede explicar mediante teorías de variables ocultas no-contextuales. ¿Puedes explicarnos esto?

-Respuesta: Lo que hemos hecho en Estocolmo es básicamente lo mismo que hicimos en Innsbruck con parejas de iones de calcio. El experimento consiste en hacer nueve preguntas diferentes sobre esos sistemas, en un caso parejas de iones, y en el otro fotones individuales agrupados de seis maneras distintas. Es decir, en cada fotón hacemos tres preguntas en diferente orden, después en otro fotón otras tres preguntas… en total, esas preguntas son de nueve tipos. Si suponemos que las respuestas a esos experimentos están de alguna manera determinadas por las propiedades del sistema o por la interacción que hacemos nosotros con el sistema, los resultados tienen que tener una cuota superior, y sin embargo la mecánica cuántica predice que sea cual sea el estado inicial de nuestro sistema, esa cuota superior se rompe, y se rompe con bastante diferencia. Por ejemplo, si es 4, esos resultados experimentales son del orden de 5 en Estocolmo.

-R: Lo curioso es que el mismo tipo de preguntas se hacen en ambos sistemas pero en Estocolmo se hacen sobre sistemas individuales, ¿qué tiene esto de especial?, que en cierto modo no es sorprendente encontrar comportamientos de este tipo en sistemas compuestos, porque existen desde hace mucho tiempo las desigualdades de Bell, que se violan para sistemas compuestos, sin embargo es la primera vez que se encuentra una cosa de este tipo para sistemas individuales. Esta es la importancia del experimento de Estocolmo.

-P: Pero cuando hablas de preguntas, te refieres a mediciones, ¿no?.

-R: Sí, mediciones. Tenemos un determinado observable físico, anotamos el resultado, a continuación sobre ese mismo sistema, otro. Además son observables sencillos, solo tienen dos posibles valores, + 1 o -1. A continuación medimos un segundo, anotamos, y a continuación medimos un tercer observable físico. Hay seis situaciones distintas, y éstas involucran nueve medidas diferentes. Son seis situaciones medidas de tres observables, uno tras otro. Hay una desigualdad que se tiene que cumplir en cualquier teoría de las llamadas de variables ocultas no-contextuales que dice que tiene que ser como mucho 4. La mecánica cuántica, en un caso ideal, si no tuviésemos ningún tipo de imperfecciones, tendría que salir 6. En el experimento, que tiene ciertas imperfecciones inevitables, no llega a salir 6, pero sale 5,5.

Sobre conjuntos mínimos de contextos cuánticos: A. Cabello, «El teorema Kochen-Specker llega al laboratorio«, Investigación y Ciencia 461 (2015) 8-9.

Wang et al, «Significant loophole-free test of Kochen-Specker contextuality using two species of atomic ions«, Science Advances 8 (2022) 1-7 ; https://arxiv.org/abs/2112.13612.

Un nuevo experimento: Contextualidad sin escapatorias; divulgación por A. Cabello.