Autofunciones monodimensionales

Formulación general del problema monodimensional

Consideremos el caso particular de la ecuación de Schrödinger para el siguiente sistema conservativo: una partícula material (no relativista) de masa $m$ y sin espín, moviéndose en el seno de un potencial real $V(x)$ (independiente de $\vec{p}$ e independiente de $t$ ), del cual se deriva la fuerza actuante según $\vec{F}(x)=-\nabla V(x)$ ; bajo estas condiciones , el Hamiltoniano clásico $H\,=\, \frac{p_x^2}{2m}+V(x)\;$ representa la energía total de la partícula.
La correspondiente ES tiene la siguiente forma:
$i\hbar\frac{\partial \Psi(x;t)}{\partial t}=H\Psi(x;t)=[-\frac{\hbar^2}{2m}\frac{d^2}{dx^2}+V(x)] \Psi(x;t)$ ,
que admite resolución por el método de separación de variables, verificándose que la ES posee soluciones de la forma separable general:
$\Psi_E(x;t)=C\,e^{-iEt/\hbar}\ \psi_E(x)$ ,
donde $C$ representa una constante arbitraria.
La ecuación diferencial para la parte espacial de la función de onda,
$[-\frac{\hbar^2}{2m}\frac{d^2}{dx^2}+V(x)]\psi(x)=E\psi(x)$
es la ecuación de Schrödinger para los estados estacionarios de energía, a menudo denominada también como ecuación de Schrödinger independiente del tiempo:
$H\psi(x)=[-\frac{\hbar^2}{2m}\frac{d^2}{dx^2}+V(x)]\psi(x)=E\psi(x)$ ,
cuya expresión es la de una ecuación de autovectores o valores propios:
$H\psi(x)=E\psi(x)$ ;
la función $\psi(x)$ se denomina función de onda independiente del tiempo.
Las funciones de onda de expresión separable $\Psi_E(x;t)=C\,e^{-iEt/\hbar}\ \psi_E(x)$ se denominan estados estacionarios de energía, y representan las soluciones de la ES
$i\hbar\frac{\partial \Psi(x;t)}{\partial t}=H_{op}\Psi(x;t)$
en el caso de un sistema conservativo (esto es, cuando el Hamiltoniano es independiente del tiempo y representa la energía total), constituyendo autofunciones del operador Hamiltoniano para los valores propios $E$ :
$H\,\Psi_E(x;t)=E\,\Psi_E(x;t)$ .
Los estados estacionarios de energía satisfacen también la ecuación:
$i\hbar\frac{\partial}{\partial t}\Psi_E(x;t)=E\,\Psi_E(x;t)$ ,
de manera que son autofunciones del operador energía $i\hbar \frac{\partial}{\partial t}$ para los valores propios o autovalores $E$ .
Las dimensiones de la función de onda monodimensional de una partícula son: $L^{-\frac{1}{2}}$ , donde $L$ simboliza longitud.

Requisitos para una función de ondas físicamente aceptable

El problema que se plantea es determinar, dado un operador Hamiltoniano, para qué autovalores $E$ (siempre reales, algo garantizado por el carácter autoadjunto del operador) se tienen autofunciones $\Psi_E(x;t)$ físicamente aceptables. La solución al problema va a establecer, bajo determinadas condiciones, la emergencia del fenómeno de la cuantización de la energía.
En el caso monodimensional de una partícula material no relativista, de masa $m \ne 0$ y sin grados de libertad internos (i.e.: sin espín), moviéndose en el seno de un potencial real $V(x)$ , independiente del tiempo, la ecuación de Schrödinger, una vez separadas las variables $x,t$ , tiene la expresión independiente del tiempo:
$H\psi(x)=[-\frac{\hbar^2}{2m}\frac{d^2}{dx^2}+V(x)]\psi(x)=E\psi(x)$ ,
$\Leftrightarrow \;\frac{d^2\psi}{dx^2}-\frac{2m}{\hbar^2}[V(x)-E]\psi(x)=0$ ,
que es una ecuación diferencial ordinaria de segundo orden, lineal y homogénea. Por tanto, su solución general, para cada $E$ , será la combinación lineal, con coeficientes constantes (escalares en principio complejos) arbitrarios, de dos soluciones particulares linealmente independientes.
Es decir, resolver el problema de valores propios
$H\psi(x)=E\psi(x)$
equivale a resolver la ecuación diferencial ordinaria (EDO)
$\frac{d^2\psi}{dx^2}-\frac{2m}{\hbar^2}[V(x)-E]\psi(x)=0$ ,
y para que el problema esté bien planteado debemos incorporar las correspondientes condiciones de contorno que permitan extraer de su solución general las soluciones particulares que las satisfagan que sean físicamente aceptables.
Como condiciones generales a imponer, dada la interpretación probabilística adoptada para la función de onda ( como densidad de probabilidad de posición, por unidad de longitud), se requerirá siempre que $\psi(x)$ sea una función unívoca y finita $\forall x \in \mathbb{R}$ . Adicionalmente, se distinguen los siguientes casos:
1. es una función continua , de manera que se implica de la EDO que también es continua . Consecuentemente, se requiere la continuidad de $\psi$ , $\psi'=\frac{d\psi}{dx}$ y $\psi''$ , $\forall \ x \in \mathbb{R}$ . En este caso, se podrán imponer dos conjuntos alternativos de condiciones de contorno adicionales:
  1. $\lim_{x \rightarrow \pm \infty} \left| \psi(x) \right| =0$ .
    Puesto que $\psi , \psi'$ $\in L^2(\mathbb{R})$ $\Rightarrow$ $\lim_{x \rightarrow \pm \infty} \left| \psi(x) \right| =0$ , estas funciones de onda se corresponderán en general con funciones del Hilbert $L^2(\mathbb{R})$ .
  2. $\lim_{x \rightarrow \pm \infty} \left| \psi(x) \right| \le C < +\infty$ , donde $C$ es una constante real, positiva y finita, $C \ge 0$ . Se exige pues que la función esté acotada a largas distancias; este caso se corresponderá con estados, como las ondas planas, que no pertenecen al espacio $L^2(\mathbb{R})$ .
    Nota: pueden existir funciones que cumplan $\lim_{ x \rightarrow \pm \infty} \left| \psi(x) \right| =0$ y no sean del Hilbert, $\psi \notin \mathscr{H}=L^2(\mathbb{R})$ : estados oscilatorios que tienden a cero a largas distancias y que sin embargo no son de cuadrado integrable, pues oscilan demasiado lejos; un ejemplo de estos estados aparece para el potencial coulombiano.
2. es una función continua a trozos con un conjunto discreto de discontinuidades de primera especie en , de manera que se implica de la EDO que también será continua a trozos y con un conjunto discreto de discontinuidades de primera especie en . En este caso, se requiere continuidad de $\psi$ y $\psi'$ , $\forall \ x \in \mathbb{R}$ , pero no de $\psi''$ . Las correspondientes condiciones de contorno adicionales a imponer podrán ser de nuevo:
  1. $\lim_{x \rightarrow \pm \infty} \left| \psi(x) \right| =0$ : $\psi , \psi'$ $\in L^2(\mathbb{R})$ .
  2. $\lim_{ x \rightarrow \pm \infty} \left| \psi(x) \right| \le C < +\infty$ , $C \ge 0$ : $\psi \notin L^2(\mathbb{R})$ .
3. es una función con discontinuidades de segunda especie en , que podrán ser de dos tipos:
  1. $V(x) \rightarrow \pm \infty$ en algunos puntos de $\mathbb{R}$ . En este caso se exigirá la anulación de la función en todos los puntos en que la función potencial $V$ se haga infinita; $\psi'$ podrá presentar en esos puntos discontinuidades de primera especie.
  2. $V(x)$ es una función que contiene en su expresión una(s) delta(s) de Dirac de la forma $\delta(x-a) \; , \, a \in \mathbb{R}$ . En estos casos se exigirá continuidad de la función $\psi$ en cada punto $a$ , pero $\psi'$ podrá presentar en ellos discontinuidades de primera especie.
Las soluciones $\psi$ de la ecuación de autovalores que pertenecen al Hilbert $\mathscr{H}=L^2(\mathbb{R})$ se dice que representan «estados ligados«. Son funciones que, una vez normalizadas de forma estándar, definen vía $| \psi |^2$ una densidad de probabilidad de posición, y que se asocian con sistemas físicos como, por ejemplo, una partícula material inicialmente bien localizada (i.e.: un paquete de ondas); otro ejemplo, una partícula confinada a moverse, por la presencia de fuerzas externas, en una región espacial bien especificada.
Los estados ligados satisfacen el Teorema de oscilación de Sturm:
1. Teorema de oscilación de Sturm: Sea una función potencial , con valor finito $\forall x \in \mathbb{R}$ , y tal que , es decir, existe un conjunto no vacío de autofunciones de la energía, . Entonces, si se ordenan los autovalores discretos de energía en orden creciente, esto es,
  ,
  siendo las respectivas autofunciones de energía
  , , …,
  se tiene que:
  1. La autofunción $\psi_{n+m}$ se anula al menos una vez $\forall m \ge 1$ .
  2. Las autofunciones de energía poseen un número creciente de ceros, de manera que la autofunción $n-$ ésima, $\psi_{n}$ posee $n$ nodos o ceros finitos (los estados ligados se anulan además todos en los límites $x \rightarrow \pm \infty$ ).
  3. Entre cada dos nodos consecutivos de $\psi_{n} \,, \,n\ge 2$ , la anterior autofunción $\psi_{n-1}$ posee un nodo.
2. Para potenciales que posean discontinuidades de segunda especie, donde por tanto las autofunciones se deben anular, el anterior teorema de oscilación se satisface de forma que los $n$ ceros de la autofunción $n-$ ésima, $\psi_{n}$ , se producen adicionalmente a los nodos en los puntos en los que el potencial se hace infinito.
  -Por ejemplo: en un caso monodimensional como el del anterior potencial de paredes infinitas o infranqueables
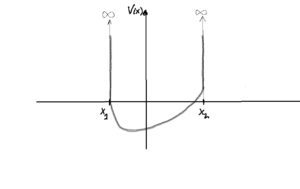  la autofunción ligada $\psi_{n}$ posee un total de $n+2$ nodos (ceros) en el intervalo $x_1 \le x \le x_2$ .
Las soluciones $\psi$ de la ecuación de autovalores que no pertenecen al Hilbert $\mathscr{H}=L^2(\mathbb{R})$ se dice que representan «estados de difusión«, o de «scattering» («colisión»), también denominados a menudo simplemente como «estados no ligados». Representan sistemas que no están ni localizados ni confinados, y para trabajar con ellos se requerirá de la introducción de formas especiales de normalización efectiva.
Obsérvese que:
1. En todos los casos a considerar, se va a requerir a las funciones $\psi$ al menos su acotación a largas distancias (en general, en cualquier dirección):
  $\lim_{ x \rightarrow \pm \infty} \left| \psi(x) \right| \le C < +\infty$ , $C$ constante real, positiva y finita, $C \ge 0$ .
2. Puesto que en la EDO obtenida tanto $E$ como $V$ son reales, para cualquier solución $\psi$ se cumplirá que su parte real $Re (\psi )= \frac{1}{2}(\psi + \psi^*)$ y su parte imaginaria $Im (\psi ) = \frac{1}{2i}(\psi - \psi^*)$ son por separado también soluciones de la EDO, y son ambas funciones reales, de forma que podemos reducirnos a considerar sólo soluciones reales del problema de valores propios planteado, sin pérdida de generalidad.
Nota matemática: para un estudio a fondo de las condiciones matemáticas a imponer sobre las funciones potencial $V(x)$ , véase [GAL-89], vol. I, cap. 4, pp. 232-238; en particular, cumplidas las condiciones matemáticas que establecen una buena formulación del problema de valores propios considerado, «se puede probar que de las soluciones $\psi$ del mismo sólo las polinómicamente acotadas y cumpliendo que $\psi, \psi'$ son absolutamente continuas son admisibles como funciones propias generalizadas del operador autoadjunto energía, y aparecen, por tanto, en su descomposición espectral», cf. p. 171.

Densidad y corriente de probabilidad

Interpretación estadística: imaginemos un gran número $n$ de sistemas idénticos e idénticamente preparados, en las mismas condiciones, compuestos cada uno por una partícula de masa $m$ ; sea $\Psi(x;t)$ la función asociada, la misma para todos ellos. Si realizamos un experimento de determinación de la posición en cada una de estas copias idénticas del mismo sistema, en un mismo elemento de línea $dx$ y en el mismo instante $t$ , se tendrá que $\lim_{n\rightarrow \infty} \frac{n(x;t)}{n}=|\Psi(x;t)|^2dx$ , siendo $n(x;t)$ el número de copias en que el resultado del experimento ha sido la detección positiva de la partícula en $dx$ .
Es decir, la colección de valores obtenidos en la medida del observable posición $x$ , o sea, las frecuencias de repetición de cada resultado posible, en el límite de muchos sistemas, $\lim{n \rightarrow \infty}$ , generan una distribución de probabilidad de la magnitud física posición. Si procedemos igual para todos los observables del sistema, tendremos caracterizado operacionalmente al sistema de la forma máxima posible, en términos predictivos.
Respecto a la medida simultánea a la posición (en este caso) de otros observables sobre el sistema, se dan dos situaciones: 1) Los observables compatibles no tendrán limitación fundamental a la precisión con que pudieran ser medidos; 2) Los observables complementarios sólo podrían ser determinados con una precisión que cumpla la correspondiente relación de indeterminación que liga el producto de las varianzas de los dos operadores a medir simultáneamente (posición y este segundo complementario).
El vector densidad de corriente monodimensional $\vec{j}(x;t)$ se define según
$\vec{j}(x;t)= -\frac{i\hbar}{2m}[ \Psi^*( \frac{d}{dx} \Psi)-(\frac{d}{dx}\Psi^*) \Psi ]\hat{i} =Re\{ -\frac{i\hbar}{m}\Psi^*( \frac{d}{dx} \Psi) \}\hat{i}$
teniéndose
$\frac{d}{dx}j(x;t)= -\frac{i\hbar}{2m}[ \Psi^*( \frac{d^2}{dx^2} \Psi)-(\frac{d^2}{dx^2}\Psi^*) \Psi ]$ ;
la correspondiente ecuación de continuidad tiene la expresión:
$\frac{\partial \left|\Psi(x;t)\right|^2}{\partial t}+\nabla \cdot \vec{j}(x;t)=0$ ,
a satisfacer por toda función de onda solución de la ES para un potencial $V(x;t)$ real.
En particular, para un estado estacionario , se tiene (caso potencial independiente del tiempo):
1. Densidad de probabilidad:
  $\left|\Psi_E(x;t)\right|^2=\left|\psi_E(x)\right|^2 \ne f(t)$
2. Corriente de probabilidad:
  $\vec{j}(x;t)= -\frac{i\hbar}{2m}[ \Psi_E^*( \frac{d}{dx} \Psi_E)-(\frac{d}{dx}\Psi_E^*) \Psi_E]\hat{i} = \vec{j}(x)=j \ \hat{i}$ , donde $j \ne f(t)$ y $j \ne f(x)$ .
3. Ecuación de continuidad:
  -Para estos estados, resulta:
  $\nabla \cdot \vec{j}=-\frac{\partial}{\partial t}P(x;t)=\frac{\partial j}{\partial x}=0$
  (corriente solenoidal).

Autofunciones monodimensionales

Autofunciones y Paridad:
1. La operación paridad se define como la reflexión espacial en torno al origen, y se representa por un operador paridad $P$ , actuando en el espacio de configuración según
  $P\Psi(x;t)=\Psi(-x;t)$ .
2. Considerado el espacio de Hilbert $\mathscr{H}=L^2(\mathbb{R})$ , el operador paridad es acotado; con norma unidad; isométrico; autoadjunto; unitario; con espectro $\sigma(P)=\sigma_p(P)=\{+1,-1\}$ .
3. Una función de onda se dice que posee paridad bien definida cuando es autofunción del operador Paridad, esto es, satisface:
  $P\Psi(x;t)=\Psi(-x;t)=\pm \Psi(x;t)$
  (para ello debe tener un intervalo de definición simétrico respecto al origen, de modo que, si se ha procedido a una normalización por confinamiento, se supone que el intervalo de la recta real considerado, de longitud $L$ , es simétrico en torno al origen ).
4. Una función de onda se define como par cuando es autofunción del operador Paridad con autovalor $+1$ .
5. Una función de onda se define como impar cuando es autofunción del operador Paridad $P$ con autovalor $-1$ .
6. Un operador $A$ se define como simétrico cuando conmuta con el operador paridad $P$ , es decir, $[A,P]=0$ . Por ejemplo, el Hamiltoniano del oscilador armónico es un operador simétrico. La situación se describe diciendo que un operador simétrico es invariante bajo la operación de paridad o inversión espacial.
7. Cuando el Hamiltoniano de un sistema es invariante bajo paridad, $[H,P]=0$ , de modo que el operador Paridad, puesto que tampoco presenta dependencia temporal explícita, $P \ne P(t)$ , constituye una constante del movimiento; en consecuencia, la paridad de los estados se conserva en la evolución temporal.
  -Además, para un sistema conservativo, cuando $[H,P]=0$ puede construirse una base de autofunciones comunes a ambos operadores: compuesta por autofunciones de energía con paridad definida.
8. Nota: En tres dimensiones, todo potencial escalar (dependencia $V(r)$ , sólo de $r=|\vec{r}|$ ) define un Hamiltoniano invariante bajo paridad.
Sea la ecuación de Schrödinger para un potencial monodimensional independiente del tiempo y simétrico, $V=V(x)=V(-x)$ (siempre con el intervalo de la recta real considerado simétrico en torno al origen), es decir, $[H,P]=0$ , el Hamiltoniano es invariante bajo paridad:
$i\hbar\frac{\partial \Psi(x;t)}{\partial t}=H\Psi(x;t)=[-\frac{\hbar^2}{2m}\frac{d^2}{dx^2}+V(x)] \Psi(x;t)$ .
Separando variables se obtiene la ecuación de autovalores:
$H\psi(x)=[-\frac{\hbar^2}{2m}\frac{d^2}{dx^2}+V(x)]\psi(x)=E\psi(x)$ .
Aplicando el operador Paridad $P$ en ambos lados:
$H\psi(-x)=[-\frac{\hbar^2}{2m}\frac{d^2}{dx^2}+V(x)]\psi(-x)=E\psi(-x)$ ,
de forma que tanto $\psi(x)$ como $\psi(-x)$ son autofunciones de energía para el mismo autovalor $E$ .
Pueden ocurrir entonces dos casos:
1. El autovalor $E$ no es degenerado; entonces, necesariamente han de ser $\psi(x)$ y $\psi(-x)$ linealmente dependientes, es decir, ha de ser:
  $\psi(-x)= P\psi(x)=C \ \psi(x) \ \forall x$ ,
  donde $C$ simboliza una constante.
  Aplicando de nuevo el operador paridad,
  $\Rightarrow P\psi(-x)= P^2\psi(x)=\psi(x)=C \ P \psi(x)=C^2\psi(x) \ \forall x$
  por lo que se implica $C= \pm 1$ , de forma que este caso se corresponde con autofunciones $\psi(x)$ que tienen paridad definida.
  -Como, en particular, los estados ligados de un potencial monodimensional nunca presentan degeneración, queda establecido que, para un potencial simétrico, los estados ligados tienen siempre paridad definida.
  -Y, teniendo en cuenta el teorema de oscilación, se deriva también que, una vez ordenados en orden creciente de energía, los estados ligados de un potencial monodimensional simétrico van alternándose en paridad, siendo la autofunción del estado fundamental par (ya que una función par tiene siempre o ninguno o un número par de nodos, mientras que una función impar posee un número impar de ceros).
2. El autovalor $E$ es degenerado, en cuyo caso $\psi(x)$ y $\psi(-x)$ pueden ser linealmente independientes; en este caso, aunque tanto $\psi(x)$ como $\psi(-x)$ sean autofunciones de energía para el mismo autovalor $E$ , no se deriva que tengan que tener paridad definida (sí lo tendrán en el caso de que sean linealmente dependientes).
  -Ahora bien, si las autofunciones $\psi(x)$ y $\psi(-x)$ , correspondientes al mismo autovalor $E$ , no tienen paridad definida, siempre es posible sustituirlas por las combinaciones lineales
  $\psi_{\pm}(x)=\frac{1}{+\sqrt{2}}(\psi(x) \pm \psi(-x))$
  que sí que tienen paridad definida: $\psi_+$ es par y $\psi_-$ es impar; además, si las iniciales $\psi(x)$ y $\psi(-x)$ estaban normalizadas, las $\psi_{\pm}(x)$ también lo están.
Autofunciones generalizadas del operador momento:
Nota: supondremos siempre un dominio de definición que garantice el carácter autoadjunto del operador.
1. Sea la ecuación de autovalores del operador momento,
  $p_{xop}\psi(x)=-i\hbar \frac{d}{dx}\psi(x)=p_x\psi(x)$
  que posee solución $\forall p_x \in \mathbb{R}$ ; las autofunciones tienen la expresión
  $\psi_{p_x}(x)=Ce^{+ip_xx/\hbar}=Ce^{+ik_xx}$ ,
  que son funciones fuera del Hilbert, $\psi_{p_x} \notin \mathscr{H}=L^2(\mathbb{R})$ ; $k_x=p_x/\hbar$ es el número de ondas .
2. Es decir, el operador momento posee un espectro puramente continuo y sin degeneración que abarca toda la recta real, $\sigma(p_x)=\mathbb{R}$ ; los correspondientes autovalores y autofunciones lo son en sentido generalizado.
Autofunciones generalizadas del operador energía cinética:
Nota: supondremos siempre un dominio de definición que garantice el carácter autoadjunto del operador.
1. Sea el caso más simple de una función potencial constante, $V(x)=V_o$ , de forma que la partícula está libre: no se ejercen fuerzas sobre ella (ya que $\vec{F}=-\nabla V =0$ ). Sin pérdida de generalidad, puede considerarse $V_o=0$ , de forma que la correspondiente ecuación de autovalores toma la expresión
  $H\psi(x)=-\frac{\hbar^2}{2m}\frac{d^2}{dx^2}\psi(x)=E\psi(x)$
  $\Rightarrow \frac{d^2\psi(x)}{dx^2}+\frac{2mE}{\hbar^2}\psi(x)=0$
2. Definiendo
  $k_x=\frac{+\sqrt{2mE}}{\hbar}=+\sqrt{\frac{2m\omega}{\hbar}} , k_x>0 \,, k_x \in \mathbb{R}$ ,
  donde $E=\hbar \omega = \frac{\hbar^2k_x^2}{2m} > 0$ ,
  (el mínimo absoluto del potencial es $V_o=0$ y sólo aparecen pues soluciones físicamente aceptables cuando $E \ge 0$ ), la anterior ecuación diferencial puede escribirse como
  $\frac{d^2\psi}{dx^2}+k_x^2\psi=0$ ,
  cuya solución general tiene la expresión:
  $\psi(x)=A e^{ik_xx}+Be^{-ik_xx}=C_1cos\ k_xx +C_2 sen\ k_xx$
  con $A,B,C_1,C_2$ escalares arbitrarios.
3. Las anteriores soluciones particulares representan estados de difusión, que son funciones fuera del Hilbert: $\psi_{E} \notin \mathscr{H}=L^2(\mathbb{R})$ ; obteniéndose dos soluciones particulares linealmente independientes para cada autovalor de energía $E>0$ , que es por tanto doblemente degenerado.
  -Para $E=0$ se obtiene $\psi(x)=C_1 + C_2x$ ; imponiendo el requisito de acotación a largas distancias se deriva $C_2=0$ , de forma que se obtiene un autoestado de expresión constante, siendo el autovalor $E=0$ no degenerado.
4. Es decir, el operador energía cinética posee un espectro puramente continuo que abarca toda la semirrecta real positiva (elección $V_o=0$ ) , $\sigma(K)=[0,+\infty)$ ; todos los autovalores son doblemente degenerados a excepción del más bajo, $E=0$ ; los correspondientes autovalores y autofunciones lo son en sentido generalizado.

Ondas planas

Consideremos una partícula no relativista de masa $m \ne 0$ , sin espín, moviéndose a lo largo del eje $OX$ , con energía $E=\frac{p_x^2}{2m}$ y momento $\vec{p}=p_x\hat{i}$ bien definido; el signo de $p_x$ determina clásicamente el sentido del movimiento sobre el eje $OX$ de los dos posibles .
A cada sentido posible del movimiento sobre el eje $OX$ se le asocia una función de onda en la forma de «onda plana viajera», que se propaga en la misma dirección y sentido, con número de ondas $k=|\vec{k}|=\frac{2\pi}{\lambda}$ fijo, $\vec{p}=p_x\hat{i}=\hbar \vec{k}=\hbar k_x\hat{i}$ , de expresión
$\Psi(x;t)=Ae^{i[k_xx-\omega(k)t]}=Ae^{i[p_xx-E(p_x) t]/\hbar}=Ae^{ip_xx/\hbar}\ e^{-iE\ t/\hbar}$ ,
donde $A$ es una constante (real o compleja); el número de ondas $k$ y la frecuencia vienen dados por la relación de de Broglie, $k=\frac{2\pi}{\lambda}=\frac{p}{\hbar}$ y $\omega=2\pi\nu=\frac{E}{\hbar}$ .
-Este tipo de funciones de onda se usan, por ejemplo, en teoría de colisiones, y aparecen al discutir la parte continua del espectro.
Para una onda distinguimos entre la velocidad de fase, $v_f=\frac{\omega(k)}{k}$ , que es la velocidad a la cual la fase de cualquier componente en frecuencia de la onda se propaga (puede ser distinta para cada frecuencia; por ejemplo, en el paquete de ondas para una partícula material así ocurre), y la velocidad de grupo, $v_g=\frac{\partial \omega (k)}{\partial k}$ , que es la velocidad a la que se desplaza la energía contenida en la onda.
Para una partícula material libre no relativista, $E=\frac{p^2}{2m}=\frac{p_x^2}{2m}$ , por lo que $\omega(k)=\frac{E(p)}{\hbar}=\frac{E(k)}{\hbar}=\frac{ \hbar k^2}{2m}$ , resultando pues $v_f=\frac{\hbar k}{2m}$ y $v_g=\frac{\hbar k}{m}$ .
La función de onda
$\Psi(x;t)=Ae^{i[p_xx-E(p_x)t]/ \hbar}$
satisface el par de ecuaciones diferenciales
$-i\hbar\frac{\partial }{\partial x}\Psi(x;t)=p_x\Psi(x;t)$
$i\hbar\frac{\partial }{\partial t}\Psi(x;t)=E\Psi(x;t)$
que justifican que, para una partícula libre de masa $m$ (no relativista), la energía y el momento pueden representarse por sendos operadores diferenciales $E_{op}=i\hbar\frac{\partial}{\partial t}$ y $p_{xop}= -i\hbar\frac{d}{dx}$ , actuando sobre la función de onda $\Psi(x;t)$ . Esta asociación constituye un postulado de la Mecánica Cuántica, que se establece para toda partícula, libre y no libre.
La función de onda de expresión

,
donde vamos a fijar el signo ,
es la solución general de la ecuación de Schrödinger para una partícula libre con energía y momento , donde y representan escalares arbitrarios. Algunos casos posibles son:
1. $B = 0$ :
  La solución particular correspondiente es el estado estacionario
  $\Psi(x;t)=Ae^{i(k_xx-\omega t)}=Ae^{ik_xx}e^{-iE t/\hbar}$ ,
  es decir, una onda plana asociada a una partícula que se desplaza en el sentido positivo del eje $OX$ , con momento $\vec{p}=\hbar \vec{k}=\hbar k_x \hat{i}=p_x\hat{i}$ , $p_x >0$ (se ha fijado $k_x >0$ ) .
  
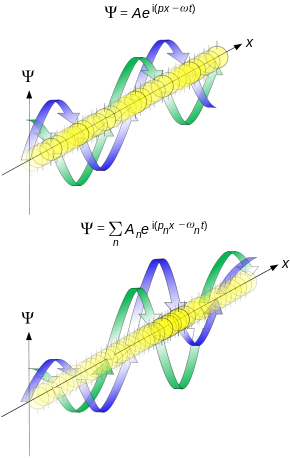
  Propagation of de Broglie waves in 1d – real part of the complex amplitude is blue, imaginary part is green. The probability (shown as the colour opacity) of finding the particle at a given point x is spread out like a waveform, there is no definite position of the particle. As the amplitude increases above zero the curvature decreases, so the decreases again, and vice versa – the result is an alternating amplitude: a wave. Top: Plane wave. Bottom: Wave packet. Imagen y pie de figura de la Wikipedia.
  
  -La densidad de probabilidad es $|A|^2$ y la corriente de probabilidad resulta $\vec{j}(x;t)=\vec{v}|A|^2$ , con $\vec{v}=v_x\hat{i}=\frac{p_x}{m}\hat{i}$ .
2. $A=0$ :
  La solución particular correspondiente es el estado estacionario
  $\Psi(x;t)=Be^{-i(k_xx+\omega t)}=Be^{-ik_xx}e^{-iE t/\hbar}$ ,
  es decir, una onda plana asociada a una partícula que se desplaza en el sentido negativo del eje $OX$ , con momento $\vec{p}=\hbar \vec{k}=-\hbar k_x \hat{i}=-p_x\hat{i}$ , $p_x >0$ (se ha fijado $k_x >0$ ) .
  -La densidad de probabilidad es $|B|^2$ y la corriente de probabilidad resulta $\vec{j}(x;t)=\vec{v}|B|^2$ , con $\vec{v}=-v_x\hat{i}=-\frac{p_x}{m}\hat{i}$ .
3. $A=B$ :
  $\Psi(x;t)=Ae^{i(k_xx-\omega t)}+Ae^{-i(k_xx+\omega t)}$
  $=A(e^{ik_xx}+e^{-ik_xx})e^{-i\omega t}$
  $=2Acos\ k_xx \ e^{-i\omega t}$ ,
  que representa una onda estacionaria (no viajera), con nodos en los puntos
  $x_n=\pm\frac{(2n+1)\pi}{2k_x}\,,\,n=0,\pm 1,\pm 2 \ldots$ , en los cuales la partícula nunca puede ser encontrada. La onda estacionaria es resultado de la superposición o interferencia de sendas ondas viajeras, en los dos sentidos opuestos posibles.
  -La densidad de probabilidad es $P(x;t)=|\Psi(x;t)|^2=4|A|^2cos^2k_xx$ y la corriente de probabilidad se anula, $\vec{j}(x;t)=0$ .
4. $A=-B$ :
  $\Psi(x;t)=Ae^{i(k_xx-\omega t)}-Ae^{-i(k_xx+\omega t)}$
  $=A(e^{ik_xx}-e^{-ik_xx})e^{-i\omega t}$
  $=2iAsen\ k_xx \ e^{-i\omega t}$ ,
  que representa una onda estacionaria (no viajera), con nodos en los puntos
  $x_n=\pm\frac{n\pi}{k_x}\,,\,n=0,\pm 1,\pm 2 \ldots$ , en los cuales la partícula nunca puede ser encontrada. La onda estacionaria es resultado de la superposición o interferencia de sendas ondas viajeras, en los dos sentidos opuestos posibles.
  -La densidad de probabilidad es $P(x;t)=|\Psi(x;t)|^2=4|A|^2sen^2k_xx$ y la corriente de probabilidad se anula, $\vec{j}(x;t)=0$ .
5. Caso general:
  $\Psi(x;t)=Ae^{i(k_xx-\omega t)}+Be^{-i(k_xx+\omega t)}$
  $=(Ae^{ik_xx}+Be^{-ik_xx})e^{-i\omega t}$ ,
  que representa una superposición de sendas ondas planas viajeras, en los dos sentidos opuestos posibles a lo largo del eje $OX$ , con amplitudes respectivas $|A|^2$ y $|B|^2$ .
  -Como los dos sumandos son estados estacionarios pertenecientes al mismo valor de energía $E=\frac{\hbar^2k_x^2}{2m}$ , su suma es también otro estado estacionario.
  -La densidad de probabilidad es:
  $P(x;t)=|\Psi(x;t)|^2=|A|^2+|B|^2+(AB^*e^{2ik_xx}A^*Be^{-2ik_xx})=|A|^2+|B|^2+2\ Re(AB^*e^{2ik_xx})$
  -La corriente de probabilidad resulta:
  $\vec{j}(x;t)=\frac{\hbar k_x}{m}(|A|^2-|B|^2)\hat{i}$
  $=\frac{p_x}{m}(|A|^2-|B|^2)\hat{i}$
6. Visualmente (pero recuérdese que las ondas cuánticas son, en general, complejas: poseen parte real e imaginaria):
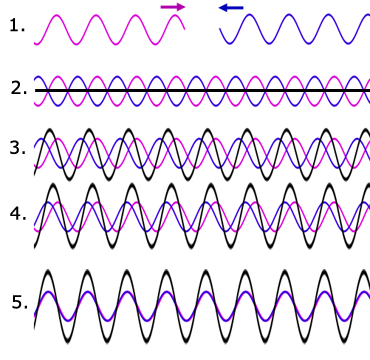
  1. Two waves having the same amplitudes approach each other from opposite directions. 2. The two waves are 180º out of phase with each other and therefore cancel out(black horizontal line). 3. The phase difference between the two waves narrows. The resultant grows but is not in phase with either of the two waves. 4. The phase difference between the two waves is narrower still. The resultant is larger but is still out of phase with the two waves. 5. The phase difference between the two waves is now zero. The resultant has its maximum value and is in phase with the two waves. (Imagen y pie de figura de: http://www.a-levelphysicstutor.com/wav-stat-wavs.php).

Normalización

La condición de normalización para las funciones de onda del tipo ondas planas presenta el problema de que es imposible satisfacer el requisito
,
ya que las correspondientes integrales resultan ser divergentes (no son funciones del Hilbert; constituyen autofunciones generalizadas). Para acometer su normalización se aplican diversos procedimientos; algunos de ellos son (hay más):
1. Dado que $\left|\Psi(x;t)\right|^2=|A|^2$ , esto es, hay igual probabilidad de encontrar a la partícula en cualquier punto del espacio, esta onda plana se asocia con el estado de preparación de la partícula en que ésta tiene un momento perfectamente definido y está completamente deslocalizada. Para que la partícula que presente alguna localización, hay que introducir alguna indeterminación en su momento: superponer ondas elementales, ondas planas, correspondientes a distintos valores del momento de la partícula: formar un «paquete de ondas«, localizado ya espacialmente y, por tanto, admitiendo normalización a la unidad vía una integración a toda la recta real $\mathbb{R}$ . Su expresión general (caso no relativista) es:
  $\Psi(x,;t)=\frac{1}{\sqrt{2\pi \hbar}}\int_{-\infty}^{+\infty}e^{i(p_xx-E(p_x) t)/\hbar}\phi(p_x)dp_x$ , con $E(p_x)=\frac{p_x^2}{2m}$ ,
  pudiendo expresarse
  $\Psi(x;t)=\frac{1}{\sqrt{2\pi \hbar}}\int_{-\infty}^{+\infty}e^{ip_xx/\hbar}e^{-iE(p_x) t/\hbar}\phi(p_x)dp_x=\mathscr{F}^{-1}\{\Phi (p_x;t) \}$
  -Es decir: el paquete es la transformada de Fourier inversa de la función $\Phi (p_x;t)=e^{-iE(p_x)\ t/\hbar}\phi(p_x)$ , esto es, de un estado estacionario de energía (espacio de momentos), y es una función del Hilbert, $\Psi(x,t) \in L^2(\mathbb{R})$ .
  -En resumen: el paquete de ondas, o superposición de muchas ondas planas, constituye una función del Hilbert $\mathscr{H}=L^2(\mathbb{R}^n)$ ( $n=1$ para el caso monodimensional), es decir, una función de cuadrado integrable Lebesgue. Para una partícula material libre, masa invariante $m_o \ne 0$ , moviéndose a lo largo del eje $OX$ con energía en aproximación no relativista ( $m=m_o$ ) $E=\frac{p_x^2}{2m}$ y momento $\vec{p}=p_x\hat{i}$ ( $|\vec{p}|=|p_x|$ ), el paquete de onda asociado tiene la expresión general (caso monodimensional):
  $\Psi(x;t)=\frac{1}{\sqrt{2\pi \hbar}}\int_{-\infty}^{+\infty}\phi(p_x)e^{i(p_xx-E(p_x) t)/\hbar}dp_x$ ,
  donde cada onda plana individual $j$ -ésima tendrá una velocidad de fase distinta, dada por $(v_{f})_j=(\frac{x}{t})_j=\frac{\omega (k_j)}{k_j}=\frac{E_j(p_{xj})}{p_{xj}}=\frac{p_{xj}}{2m}=\frac{\hbar k_j}{2m}$ ; $\phi(p_x)$ es la correspondiente función de distribución de momentos, que para la partícula libre puede escogerse como una gaussiana con un pico muy acusado, por ejemplo.
  -Su representación: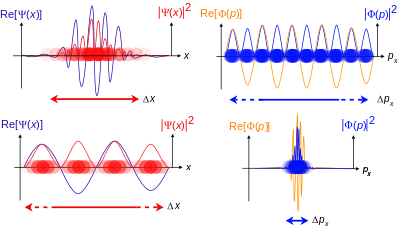
  
  Wave function for one spin-0 particle in one dimension; increasing amounts of wavepacket localization, meaning the particle becomes more localized. The wavefunctions shown are continuous, finite, single-valued and normalized. The colour opacity (%) of the particles corresponds to the probability density (which can measure in %) of finding the particle at the points on the x-axis. In the limit ħ → 0, the particle’s position and momentum become known exactly. Imagen y pie de figura de la Wikipedia.
2. Otra posibilidad es la normalización por confinamiento: restringir la integral a una región muy extensa, de dimensión lineal $L$ : integrar sobre un subintervalo $L \subset \mathbb{R}$ , muy grande pero finito, sobre cuya frontera o extremos se impone la condición de contorno apropiada para la función de onda. De esta forma, se convierte la parte continua del espectro, en su caso, en parte cuasi-continua (discreta), y la condición de normalización pasa a ser
  $\int_{L}\left|\Psi(x;t)\right|^2dx=1$ .
  -En el caso de las ondas planas, las condiciones de frontera no pueden ser de anulación en los extremos del intervalo de longitud $L$ , por lo que se recurre a establecer condiciones de contorno periódicas, del tipo $\psi(x)=\psi(x+L)$ .
  -Por ejemplo, para k-ondas planas monodimensionales, $\psi(x)=e^{ik_xx}$ , esta condición conduciría a
  $e^{ik_xx}=e^{ik_x(x+L)} \, \Rightarrow e^{ik_xL}=1$
  $\Rightarrow k_xL=2\pi n \, \Rightarrow k_x=\frac{2\pi}{L}n\,,\,n=0,\pm 1,\pm 2 \ldots$
  derivándose para la energía la cuantización
  $E_n=\frac{\hbar^2 k_x^2}{2m}=\frac{2\pi^2 \hbar^2}{mL^2} n^2\,,\,n=0,\pm 1,\pm 2 \ldots$ .
  Es decir, surge una discretización en el continuo, que ha devenido en casi-continuo; a mayor dimensión $L$ , más fina esta discretización.
  -La normalización exige funciones de onda de la forma $\psi_N(x)=Ne^{ik_xx}$ tales que
  $\int_{L}^{2L} \psi_N^*(x)\psi_N(x)\ dx=\int_{L}^{2L} e^{-ik_xx}e^{ik_xx}\ dx=N^2L=1$
  es decir, las funciones normalizadas serían $\psi(x)=\frac{1}{\sqrt{L}}e^{ik_xx}$ .
3. Otra posibilidad, muy frecuente, es recurrir a la normalización vía la delta de Dirac:
  $\delta(x)=\frac{1}{2\pi}\int_{-\infty}^{+\infty} e^{ik_xx}\ dk_x$
  $\delta(k_x'-k_x)=\frac{1}{2\pi}\int_{-\infty}^{+\infty} e^{i(k_x'-k_x)x}\ dx$
  Por ejemplo:
  $\int_{-\infty}^{+\infty} \psi_{k_x'}^*(x)\psi_{k_x}(x)\ dx=\delta(k_x'-k_x)$
  $\int_{-\infty}^{+\infty} \psi_{p_x'}^*(x)\psi_{p_x}(x)\ dx=\delta(p_x'-p_x)$
  $\int_{-\infty}^{+\infty} \psi_{E'}^*(x)\psi_{E}(x)\ dx=\delta(E'-E)$
  denominadas, respectivamente como $k-$ normalización, $p-$ normalización y $E-$ normalización.
  -Las correspondientes autofunciones normalizadas se expresan:
  $\psi_{k_x}(x)=\frac{1}{\sqrt{2\pi}}e^{ik_xx}$
  $\psi_{p_x}(x)=\frac{1}{\sqrt{2\pi \hbar}}e^{ip_xx/\hbar}$
  $\psi_{E_ {\pm}}(x)=\frac{1}{\sqrt{2\pi \hbar}} (\frac{m}{2E})^{\frac{1}{4}}e^{\pm i\frac{+\sqrt{2mE}}{\hbar}x}$ ( $E=\hbar \omega = \frac{\hbar^2k_x^2}{2m} > 0$ ).
  -Y las correspondientes relaciones de cierre o clausura:
  $\int_{-\infty}^{+\infty} \psi_{k_x}^*(x')\psi_{k_x}(x)\ dk_x=\frac{1}{2\pi}\int_{-\infty}^{+\infty} e^{-ik_xx'}e^{ik_xx}\ dk_x=\delta(x'-x)$
  $\int_{-\infty}^{+\infty} \psi_{p_x'}^*(x)\psi_{p_x}(x)\ dp_x=\frac{1}{2\pi \hbar}\int_{-\infty}^{+\infty} e^{-ip_xx'/\hbar} e^{ip_xx/\hbar}\ dp_x=\delta(x'-x)$
  $\int_{-\infty}^{+\infty} \psi_{E}^*(x')\psi_{E}(x)\ dE$
  $= \frac{1}{2\pi \hbar}(\frac{m}{2E})^{\frac{1}{2}} \int_{-\infty}^{+\infty} e^{\mp i\frac{+\sqrt{2mE}}{\hbar}x'}e^{\pm i\frac{+\sqrt{2mE}}{\hbar}x}\ dE=\delta(x'-x)$ .