Variables ocultas: concepto e historia
![]() Una «variable oculta», V.O., es una variable que se asume como desconocida y que se incorpora a una teoría con el fin de ampliarla. En el caso de la teoría cuántica, y asumiendo como correcta la acusación EPR de que constituye una teoría incompleta, incorporar postuladas V.O. es un intento de afinarla, en primer lugar para completarla y, en muchos casos, para también, en segundo lugar, superar su carácter estocástico, o sea, recuperar el determinismo perdido.
Una «variable oculta», V.O., es una variable que se asume como desconocida y que se incorpora a una teoría con el fin de ampliarla. En el caso de la teoría cuántica, y asumiendo como correcta la acusación EPR de que constituye una teoría incompleta, incorporar postuladas V.O. es un intento de afinarla, en primer lugar para completarla y, en muchos casos, para también, en segundo lugar, superar su carácter estocástico, o sea, recuperar el determinismo perdido.
![]() Por tanto, una teoría cuántica de variables ocultas es una teoría que, incorporando V.O., se propone plantearse como una compleción a la M.C.
Por tanto, una teoría cuántica de variables ocultas es una teoría que, incorporando V.O., se propone plantearse como una compleción a la M.C.
![]() Una referencia esencial al respecto es la siguiente:
Una referencia esencial al respecto es la siguiente:
![]() E. Santos, The Search for Hidden Variables in Quantum Mechanics, en [SEL-88], pp. 365-390.
E. Santos, The Search for Hidden Variables in Quantum Mechanics, en [SEL-88], pp. 365-390.
![]() Premisa: «La mecánica cuántica es una teoría incompleta»
Premisa: «La mecánica cuántica es una teoría incompleta»
![]() Reacciones posibles:
Reacciones posibles:
1. No aceptarlo: → interpretación de Copenhague.
2. Aceptarlo: En este caso se puede, de forma compatible:
2.a) Rechazar por completo la teoría cuántica, no por incorrecta o inválida, sino por insuficiente (Einstein).
2.b) Intentar su compleción, extensión o refinamiento, esto es, completarla: → proponentes de variables ocultas (¿Einstein?, Bohm,…).
-A continuación, vamos a desarrollar la historia de la segunda alternativa 2.b) anterior:
![]() Concepto de variable oculta (V.O.):
Concepto de variable oculta (V.O.):
«Variables ocultas» (V.O.): parámetros no accesibles experimentalmente (“por hoy”) que, añadidos a la mecánica cuántica (“ortodoxa”), permitirían a la teoría, principalmente: a) efectuar predicciones siempre certeras sobre los resultados individuales de los experimentos, superando la descripción meramente estadística; y/o b) convertir a la teoría cuántica en un tipo de teoría más cercano a la tradición clásica científica (realismo); c) otros…
-Obsérvese que, por supuesto, sería posible el considerar V.O. estocásticas sólo con el propósito b) anterior: → salvar el realismo aunque no el determinismo.
«Teoría de variables ocultas» (Teoría de V.O.) «óptima»: Teoría que, conservando todas las predicciones estadísticas de la M.C., se propone “ir más allá”, acometiendo una descripción que especifique los resultados para los experimentos individuales y/o permita recuperar el realismo científico.
![]()
Aclaraciones y comentarios:
- En definitiva, ya que a partir de la función de onda ψ que describe en M.C. el estado de un sistema sólo se puede, en general, hacer predicciones de tipo estadístico para los resultados de las medidas de los observables, puede considerarse que los sistemas del ensemble, o conjunto para el que la M.C. realiza sus predicciones estadísticas, difieren entre sí en el valor de unos parámetros adicionales, λ, las V.O.
- Esto es: se incorporan a la descripción teórica unos microestados que dependen de las V.O.: unos ψ = ψ(λi), i = 1,2,…, → microestados o estados libres de dispersión para todo observable de la M.C.
- Por tanto, si se lograse acceso experimental a la naturaleza y valores específicos de estas nuevas V.O., para cada microestado, los distintos sistemas del ensemble se harían distinguibles entre sí, y sería posible predecir los resultados de las medidas de los observables sobre cada sistema individual que integra el colectivo estadístico o ensemble.
- Repárese en que, obviamente, también podría suceder, es una posibilidad más, que todos los sistemas del ensemble estuvieran en el mismo estado (iguales valores para todas las λ en todos los microestados correspondientes a cada estado del ensemble), con lo que las leyes de la naturaleza no serían en última instancia deterministas y las V.O. serían, después de todo, unos entes superfluos e innecesarios de los que prescindir (a efectos de cálculos, o sea, para realizar predicciones sobre resultados experimentales).
- A priori, parece sensato plantear, siguiendo una línea de pensamiento positivista, que un requisito básico a pedir a una teoría de V.O. es ser capaz de establecer una prueba empírica a su favor; en otras palabras: no ser observacionalmente equivalente a la M.C.
- Porque, si lo fuera, lo que convertiría a esas V.O. en inobservables, metafísicas, deberíamos desestimarla en aras de la simplicidad y economía postulacional (navaja de Occam), criterios tradicionalmente aceptados (¿de forma unánime?) para elegir entre dos teorías experimentalmente equivalentes.
- Pero… ¿y si una teoría de V.O., aun siendo observacionalmente equivalente a la M.C. (ortodoxa), fuera capaz de resolver problemas conceptuales, o de interpretación, de esta? (supuesto los tiene, lo que admite muy controvertido debate, desde luego).
- Algunos físicos, entre los que creen que existen esos problemas, evidentemente, estarían dispuestos a sacrificar la simplicidad conceptual si fuera posible concebir una descripción de la naturaleza, la inherente a esa teoría, que estuviese más de acuerdo con sus supuestos filosóficos, aunque no fuese, hoy por hoy, útil. Además, siempre se podría calcular, desarrollar las aplicaciones, con la versión ortodoxa, reducida en este caso a mera herramienta de cálculo y desprovista de cualquier pretensión de describir la naturaleza “tal como es”… Lo único que ya pretende la versión ortodoxa, por otra parte, declaradamente instrumentalista.
- Y, además, quién sabe, un ulterior desarrollo tecnológico podría hacer en un futuro medibles esas V.O. , rompiendo la equivalencia observacional e, incluso, desterrando el indeterminismo.
![]()
La controversia sobre las V.O.:
![]() Tanto Born como Heisenberg, en sus artículos básicos “demoledores” del indeterminismo, sobre la interpretación probabilística de ψ y las relaciones de indeterminación, aludieron ya a la posible concepción de V.O., expresándose:
Tanto Born como Heisenberg, en sus artículos básicos “demoledores” del indeterminismo, sobre la interpretación probabilística de ψ y las relaciones de indeterminación, aludieron ya a la posible concepción de V.O., expresándose:
a) Born como conciliador y abierto a un posible debate:
![]() M. Born, «Zur Quantenmechanik der Stossvorgänge», Zeitschrift für Physik 37 (1926) 863-867, 38 (1926) 803-827:
M. Born, «Zur Quantenmechanik der Stossvorgänge», Zeitschrift für Physik 37 (1926) 863-867, 38 (1926) 803-827:
![]() Here the whole problem of the determinism comes up. From the standpoint of our quantum mechanics there is no quantity which in any individual case causally fixes the consequence of the collision; but also experimentally we have so far no reason to believe that there are some inner properties of the atom which condition a definite outcome for the collision. Ought we to hope later to discover such properties (like phases or the internal atomic motions) and determine them in individual cases? Or ought we to believe that the agreement of theory and experiment -as to the impossibility of prescribing conditions for a causal evolution- is a pre-established harmony founded on the no existence of such conditions? I myself am inclined to give up determinism in the world of atoms. But that is a philosophical question for which physical arguments alone are not decisive.
Here the whole problem of the determinism comes up. From the standpoint of our quantum mechanics there is no quantity which in any individual case causally fixes the consequence of the collision; but also experimentally we have so far no reason to believe that there are some inner properties of the atom which condition a definite outcome for the collision. Ought we to hope later to discover such properties (like phases or the internal atomic motions) and determine them in individual cases? Or ought we to believe that the agreement of theory and experiment -as to the impossibility of prescribing conditions for a causal evolution- is a pre-established harmony founded on the no existence of such conditions? I myself am inclined to give up determinism in the world of atoms. But that is a philosophical question for which physical arguments alone are not decisive.
b) Heisenberg como tajantemente desestimador:
![]() W. Heisenberg, » Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik», Zeitschrift für Physik 43 (1927) 172-198; trad. al inglés en [WHE-83], pp. 62-84, «The physical content of Quantum Kinematics and Mechanics» :
W. Heisenberg, » Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik», Zeitschrift für Physik 43 (1927) 172-198; trad. al inglés en [WHE-83], pp. 62-84, «The physical content of Quantum Kinematics and Mechanics» :
![]() But what is wrong in the sharp formulation of the law of causality, ‘When we know the present precisely, we can predict the future’, is not the conclusion but the assumption. Even in principle we cannot know the present in all detail. For that reason everything observed is a selection from a plenitude of possibilities and a limitation on what is possible in the future. As the statistical character of quantum theory is so closely linked to the inexactness of all perceptions, one might be led to the presumption that behind the perceived statistical world there still hides a `real’ world in which causality holds. But such speculations seem to us, to say it explicitly, fruitless and senseless. Physics ought to describe only the correlation of observations. One can express the true state of affairs better in this way: Because all experiments are subject to the laws of quantum mechanics, and therefore to equation Δp Δq ≈ h, it follows that quantum mechanics establishes the final failure of causality.
But what is wrong in the sharp formulation of the law of causality, ‘When we know the present precisely, we can predict the future’, is not the conclusion but the assumption. Even in principle we cannot know the present in all detail. For that reason everything observed is a selection from a plenitude of possibilities and a limitation on what is possible in the future. As the statistical character of quantum theory is so closely linked to the inexactness of all perceptions, one might be led to the presumption that behind the perceived statistical world there still hides a `real’ world in which causality holds. But such speculations seem to us, to say it explicitly, fruitless and senseless. Physics ought to describe only the correlation of observations. One can express the true state of affairs better in this way: Because all experiments are subject to the laws of quantum mechanics, and therefore to equation Δp Δq ≈ h, it follows that quantum mechanics establishes the final failure of causality.
![]()
Antecedentes históricos:
- Según M. Jammer, la idea de V.O. es antigua en la historia del pensamiento (consultar [JAM-74], pp. 257 ss.).
- En efecto: definida una teoría de V.O. como una teoría que, en esencia, “racionaliza” la conducta de un sistema en términos de parámetros que, por las razones que sea, son inaccesibles experimentalmente, su existencia es antigua, yendo acompañada históricamente por el debate en torno a su conveniencia o sentido.
- Ejemplos muy conocidos son:
a) La teoría de la visión de Arquitas de Tarento, s. –IV, que introducía “rayos ópticos”.
b) La teoría atomista antigua, y la oposición mostrada por Aristóteles, que la afirmaba como lógicamente insostenible y metodológicamente innecesaria.
c) Siglo XX: las moléculas, con las que Boltzmann era partidario de interpretar mecánico-cinéticamente los fenómenos termodinámicos, y a las que Mach y otros se opusieron radicalmente.
- En teoría cuántica, la primera teoría de V.O. parece que se remonta a 1926, siendo atribuida a Frenkel. De ella sólo quedan vagas referencias hechas por Born (ver [JAM-74], pp. 263-265, donde intenta su reconstrucción).
![]()
Einstein y las variables ocultas:
- Aparentemente, las tesis y propósitos que acompañan las V.O. coincidirían con los objetivos de Einstein respecto a la M.C. y, de hecho, las V.O. toman impulso a partir del teorema EPR.
- Sin embargo, existe un debate sobre si Einstein abogaba por ellas o no:
a) Jammer sostiene ([JAM-74], p. 254) que Einstein no era un proponente de V.O., contra lo manifestado por J.S. Bell en su “muy leído” artículo “On the EPR paradox”, que comienza con la frase:
![]() J.S. Bell, “On the EPR paradox”, Physics 1 (1964) 195-200; trad. en [BEL-90], pp. 41-50:
J.S. Bell, “On the EPR paradox”, Physics 1 (1964) 195-200; trad. en [BEL-90], pp. 41-50:
![]() La paradoja EPR se propuso como un argumento de que la M.C. no podía ser una teoría completa, sino que debía ser suplida con variables adicionales, que restauraran la localidad y la causalidad en la teoría.
La paradoja EPR se propuso como un argumento de que la M.C. no podía ser una teoría completa, sino que debía ser suplida con variables adicionales, que restauraran la localidad y la causalidad en la teoría.
![]() En opinión de Jammer, hay encuadrar a Einstein entre los que se pronunciaban a favor de, más que completar la M.C., sustituirla por una teoría alternativa radicalmente diferente (teoría de campos unificada).
En opinión de Jammer, hay encuadrar a Einstein entre los que se pronunciaban a favor de, más que completar la M.C., sustituirla por una teoría alternativa radicalmente diferente (teoría de campos unificada).
b) Bell, en su artículo:
![]() “EPR experiments”, J.S. Bell, “EPR experiments”, Proceedings of the Symposium on Frontier Problems in High Energy Physics, Pisa, junio 76, pp.33-45; trad. en [BEL-90],
“EPR experiments”, J.S. Bell, “EPR experiments”, Proceedings of the Symposium on Frontier Problems in High Energy Physics, Pisa, junio 76, pp.33-45; trad. en [BEL-90],
incluyó un apéndice en que respondía a Jammer. En opinión de Bell, el objetivo de Einstein era en efecto encontrar una teoría alternativa a la M.C., pero también consideraba que ésta podría ser completada.
![]() De hecho, existen referencias sobre el esbozo por Einstein de alguna teoría de V.O., aunque no llegara a publicarla:
De hecho, existen referencias sobre el esbozo por Einstein de alguna teoría de V.O., aunque no llegara a publicarla:
![]() D.W., Belousek, «Einstein’s 1927 Unpublished Hidden-Variable Theory: Its background, Context and Significance», Studies in History and Philosophy of Modern Physics, 27B,4 (1996) 437-461.
D.W., Belousek, «Einstein’s 1927 Unpublished Hidden-Variable Theory: Its background, Context and Significance», Studies in History and Philosophy of Modern Physics, 27B,4 (1996) 437-461.
-Pero la realidad es que, tras la famosa prueba de imposibilidad de V.O. que realizó von Neumann en 1932, el tema quedó “dormido”, hasta que D. Bohm, en 1952, conseguiría revitalizarlo.
Teoremas de imposibilidad de V.O.: enunciado y crítica
![]() Las teorías de V.O. han sido rechazadas en la filosofía y la ciencia modernas porque, al ser experimentalmente inobservables las variables involucradas, su concepción ha sido tildada de inútil y superflua, siguiendo un modo de pensamiento positivista.
Las teorías de V.O. han sido rechazadas en la filosofía y la ciencia modernas porque, al ser experimentalmente inobservables las variables involucradas, su concepción ha sido tildada de inútil y superflua, siguiendo un modo de pensamiento positivista.
![]() Además, existen teoremas matemáticos que afirman la imposibilidad de existencia para teorías de V.O. de determinados tipos.
Además, existen teoremas matemáticos que afirman la imposibilidad de existencia para teorías de V.O. de determinados tipos.
![]() Teorema de no existencia de V.O. de von Neumann
Teorema de no existencia de V.O. de von Neumann
![]() En 1932 von Neumann publicó una prueba de no existencia de V.O.: se trata del famoso «teorema de imposibilidad de V.O. de von Neumann»:
En 1932 von Neumann publicó una prueba de no existencia de V.O.: se trata del famoso «teorema de imposibilidad de V.O. de von Neumann»:
![]() J. von Neumann, J., Mathematische Grundlagen der Quantenmechanik, Springer, Berlín, 1932; Mathematical Foundations of Quantum Mechanics, Princenton Univ., Princenton, 1955; Fundamentos matemáticos de la Mecánica Cuántica, C.S.I.C., Madrid, 1991.
J. von Neumann, J., Mathematische Grundlagen der Quantenmechanik, Springer, Berlín, 1932; Mathematical Foundations of Quantum Mechanics, Princenton Univ., Princenton, 1955; Fundamentos matemáticos de la Mecánica Cuántica, C.S.I.C., Madrid, 1991.
![]() En este teorema se establece que:
En este teorema se establece que:
![]() [GAL-89], vol. I, pp. 459-460:
[GAL-89], vol. I, pp. 459-460:
![]() El aspecto estocástico de la M.C. no puede reproducirse bajo la hipótesis de que existen unos parámetros cuyo conocimiento fije un microestado de un sistema, libre de dispersión para todo observable y en términos de los cuales un estado cuántico puro ordinario Ψ no sea más que un macroestado mezcla incoherente de aquéllos (tales parámetros serían análogos a las posiciones y velocidades de todas y cada una de las moléculas de un gas, que son las que en última instancia fijan el estado termodinámico especificado por las variables observables presión, volumen y temperatura absoluta).
El aspecto estocástico de la M.C. no puede reproducirse bajo la hipótesis de que existen unos parámetros cuyo conocimiento fije un microestado de un sistema, libre de dispersión para todo observable y en términos de los cuales un estado cuántico puro ordinario Ψ no sea más que un macroestado mezcla incoherente de aquéllos (tales parámetros serían análogos a las posiciones y velocidades de todas y cada una de las moléculas de un gas, que son las que en última instancia fijan el estado termodinámico especificado por las variables observables presión, volumen y temperatura absoluta).
![]() Partiendo del contexto ordinario de la M.C., en que los observables se identifican con los operadores autoadjuntos de un espacio de Hilbert complejo y separable, y los estados cuánticos convencionales son simplemente funcionales lineales positivos sobre los observables acotados, y haciendo la hipótesis de que los microestados o estados libres de dispersión son igualmente funcionales lineales positivos sobre los observables acotados, se concluye que no existen estados libres de dispersión o microestados, o sea, que no es posible una descripción por V.O.
Partiendo del contexto ordinario de la M.C., en que los observables se identifican con los operadores autoadjuntos de un espacio de Hilbert complejo y separable, y los estados cuánticos convencionales son simplemente funcionales lineales positivos sobre los observables acotados, y haciendo la hipótesis de que los microestados o estados libres de dispersión son igualmente funcionales lineales positivos sobre los observables acotados, se concluye que no existen estados libres de dispersión o microestados, o sea, que no es posible una descripción por V.O.
-Para detalles sobre el teorema de imposibilidad de von Neumann, leáse [JAM-74], pp. 265-277; [ICA-91], pp. 238-241, y la exposición original, [NEU-91], pp. 225-233.
![]() Esquema del teorema:
Esquema del teorema:
-Premisas:
- Postulado 1: Si un observable es representado por el operador P, entonces una función f de ese observable es representado por f(P).
- Postulado 2: Si se consideran observables representados por los operadores P,S,…, entonces la suma de observables se representa por la suma de operadores P+S+…, conmuten o no entre sí dichos operadores.
- Postulado 3: Si la magnitud P es no-negativa, entonces el observable P es positivo (<P> ≥ 0).
- Postulado 4 (sobre el que Bell dirigirá su crítica): Se establece un isomorfismo entre la estructura de espacio vectorial de los observables cuánticos y la de los observables de la teoría de V.O., de forma que se tiene que si P,S,…, son observables arbitrarios y a, b,…€ R, entonces
<aP + bS + …> = a<P> + b<S> + …
tanto para los macroestados cuánticos como para los microestados de la teoría de V.O.
Conclusión del teorema von Neumann: No existen estados libres de dispersión → No es posible una descripción con V.O.
![]() En términos de M. Jammer ([JAM-74]):
En términos de M. Jammer ([JAM-74]):
![]() Si los experimentos fuerzan a basar el formalismo de la M.C. en los postulados enunciados, entonces cualquier concepción de V.O., concebida para restaurar el determinismo en la teoría, es incompatible con los postulados.
Si los experimentos fuerzan a basar el formalismo de la M.C. en los postulados enunciados, entonces cualquier concepción de V.O., concebida para restaurar el determinismo en la teoría, es incompatible con los postulados.
![]() Sobre este postulado, comentan en el manual antes citado A. Galindo y P. Pascual ([GAL-89], vol. I, p. 460):
Sobre este postulado, comentan en el manual antes citado A. Galindo y P. Pascual ([GAL-89], vol. I, p. 460):
![]() Ahora bien, si von Neumann demostró que no existen V.O., ¿para qué continuar por este camino? ¿Cómo se explica que, a pesar de la rotunda afirmación de von Neumann, bastantes científicos de reconocido prestigio, como de Broglie, Bohm, Wiener y otros hayan elaborado teorías basadas en V.O.? En realidad, la autoridad de von Neumann gravitó de tal fuerza que detuvo durante veinte años todo progreso interesante en este problema.
Ahora bien, si von Neumann demostró que no existen V.O., ¿para qué continuar por este camino? ¿Cómo se explica que, a pesar de la rotunda afirmación de von Neumann, bastantes científicos de reconocido prestigio, como de Broglie, Bohm, Wiener y otros hayan elaborado teorías basadas en V.O.? En realidad, la autoridad de von Neumann gravitó de tal fuerza que detuvo durante veinte años todo progreso interesante en este problema.
![]() En el año 1952, Bohm, por primera vez, critica el resultado de von Neumann desde el punto de vista físico, diciendo que hay algo insatisfactorio en el planteamiento que este matemático hace del problema.
En el año 1952, Bohm, por primera vez, critica el resultado de von Neumann desde el punto de vista físico, diciendo que hay algo insatisfactorio en el planteamiento que este matemático hace del problema.
![]() Pero habrá que esperar al año 1966 a que Bell ponga el dedo en la llaga, señalando la premisa concreta del teorema de von Neumann que es inaceptable a priori en cualquier teoría realista de V.O. Recordemos que, en el contexto ordinario de la M.C., los observables se identifican con los operadores autoadjuntos de un espacio de Hilbert complejo y separable, y que los estados cuánticos convencionales son simplemente funcionales positivos lineales sobre los observables acotados. Von Neumann requiere, sin más, esto mismo de los microestados, es decir, de los estados libres de dispersión. Y bajo esta hipótesis sigue su teorema.(…) Pero no hay razón a priori para exigir la linealidad de los valores esperados.
Pero habrá que esperar al año 1966 a que Bell ponga el dedo en la llaga, señalando la premisa concreta del teorema de von Neumann que es inaceptable a priori en cualquier teoría realista de V.O. Recordemos que, en el contexto ordinario de la M.C., los observables se identifican con los operadores autoadjuntos de un espacio de Hilbert complejo y separable, y que los estados cuánticos convencionales son simplemente funcionales positivos lineales sobre los observables acotados. Von Neumann requiere, sin más, esto mismo de los microestados, es decir, de los estados libres de dispersión. Y bajo esta hipótesis sigue su teorema.(…) Pero no hay razón a priori para exigir la linealidad de los valores esperados.
![]() Repercusiones:
Repercusiones:
-Así pues, la autoridad de von Neumann era tan considerable y considerada que, durante dos décadas, tras la publicación de su teorema, las V.O. fueron abandonadas como tema de investigación. Dos ejemplos ilustrativos:
- 1. Cuando en 1952 Bohm publicó su teoría de V.O., fue completamente ignorada, a pesar de que su mera existencia como teoría de V.O. determinista (no local) capaz de reproducir los resultados de la M.C. (no relativista) debiera haber suscitado la atención, al menos sobre cómo era posible su misma existencia.
- 2. Bell ha narrado como, atraído fuertemente por el argumento EPR y la posibilidad relacionada de elaborar una descripción teórica más completa que la de la M.C., en cuanto tuvo conocimiento de que von Neumann había demostrado su imposibilidad abandonó el tema. Posteriormente, sin embargo, «al ver lo imposible realizado», decidió analizar cómo era posible, es decir, si es que el teorema de von Neumann era erróneo:
 J.S. Bell, «On the impossible pilot wave», Foundations of Physics, 12 (1982) 989-999; trad. en [BEL-90], pp. 221-233.
J.S. Bell, «On the impossible pilot wave», Foundations of Physics, 12 (1982) 989-999; trad. en [BEL-90], pp. 221-233.
![]() Otros teoremas de imposibilidad de teorías de V.O.
Otros teoremas de imposibilidad de teorías de V.O.
![]() Existen otros teoremas de imposibilidad además del de von Neumann. Entre ellos, con parecidas consecuencias negativas para las V.O., pueden citarse como más conocidos el teorema de Jauch y Piron,
Existen otros teoremas de imposibilidad además del de von Neumann. Entre ellos, con parecidas consecuencias negativas para las V.O., pueden citarse como más conocidos el teorema de Jauch y Piron,
![]() J.M. Jauch and C. Piron, Helv. Phys. Acta 36 (1963) 827,
J.M. Jauch and C. Piron, Helv. Phys. Acta 36 (1963) 827,
y, especialmente, el teorema de Gleason,
![]() A.M. Gleason, J. Math. Mech., 6 (1957) 885,
A.M. Gleason, J. Math. Mech., 6 (1957) 885,
este último considerado en su momento como definitivo.
-Difieren del de von Neumann, esencialmente, en que relajan el postulado 4, exigiéndolo sólo para operadores que conmutan, y añaden hipótesis varias sobre valores esperados de determinados proyectores, hipótesis cuya validez, siendo clara para los estados de la M.C., es también supuesta para los microestados:
![]() Bell, J.S.; «On the problem of hidden variables in quantum mechanics», Reviews of Modern Physics 38 (1966) 447-452, trad. en [BEL-90], pp. 25-40.
Bell, J.S.; «On the problem of hidden variables in quantum mechanics», Reviews of Modern Physics 38 (1966) 447-452, trad. en [BEL-90], pp. 25-40.
![]() Crítica por Bell a los teoremas de imposibilidad de V.O.
Crítica por Bell a los teoremas de imposibilidad de V.O.
![]() En 1966 Bell publicó un artículo fundamental, que tenía redactado desde 1964:
En 1966 Bell publicó un artículo fundamental, que tenía redactado desde 1964:
![]() Bell, J.S.; «On the problem of hidden variables in quantum mechanics«, Reviews of Modern Physics 38 (1966) 447-452, trad. en [BEL-90], pp. 25-40.
Bell, J.S.; «On the problem of hidden variables in quantum mechanics«, Reviews of Modern Physics 38 (1966) 447-452, trad. en [BEL-90], pp. 25-40.
![]() En la introducción de este artículo, Bell afirmaba que, aunque los teoremas de imposibilidad eran mayoritariamente considerados hasta entonces como universales e invulnerables,
En la introducción de este artículo, Bell afirmaba que, aunque los teoremas de imposibilidad eran mayoritariamente considerados hasta entonces como universales e invulnerables,
![]() La conciencia de que la prueba de von Neumann es de relevancia limitada ha ido ganando terreno desde el trabajo de Bohm de 1952. Sin embargo, se halla lejos de ser universal. Además, quien escribe no ha encontrado en la literatura ningún análisis de qué era incorrecto en dicha prueba.
La conciencia de que la prueba de von Neumann es de relevancia limitada ha ido ganando terreno desde el trabajo de Bohm de 1952. Sin embargo, se halla lejos de ser universal. Además, quien escribe no ha encontrado en la literatura ningún análisis de qué era incorrecto en dicha prueba.
-Además, Bell señala la existencia de un debate sobre si la cuestión de las V.O. es interesante o no. Pero él, nos dice, no se propone contribuir a tal debate, sino sólo «clarificar lo que realmente demostraron von Neumann y sus continuadores», haciendo hincapié en que esos análisis «dejan intacta la cuestión real».
![]() Esencialmente, en su trabajo Bell señala el postulado 4 como inaceptable para los microestados, en concreto:
Esencialmente, en su trabajo Bell señala el postulado 4 como inaceptable para los microestados, en concreto:
- Contra von Neumann: El hecho de que el valor esperado de una combinación lineal de observables sea la combinación lineal de los valores esperados de los correspondientes valores esperados, cierto para los estados cuánticos, no tiene por qué requerirse para los microestados.
- Contra von Neumann y Gleason: Para los microestados, los valores esperados de los observables dependen no sólo del observable a medir, sino también del aparato particular, es decir, del montaje experimental concreto, con el que se va a realizar la medición (i.e.: qué otros observables se decida medir).
![]() En definitiva, en esta respuesta podemos intuir que Bell está incorporando el espíritu de la respuesta de Bohr a la situación EPR: el estado cuántico no puede concebirse ya como interaccional (hasta 1935), sino que ha quedado establecido como relacional (desde 1935):
En definitiva, en esta respuesta podemos intuir que Bell está incorporando el espíritu de la respuesta de Bohr a la situación EPR: el estado cuántico no puede concebirse ya como interaccional (hasta 1935), sino que ha quedado establecido como relacional (desde 1935):
![]() En texto del artículo de J.S.Bell:
En texto del artículo de J.S.Bell:

Tipos de variables ocultas
![]() Existen muchos tipos de V.O., es decir, de teorías que, incorporando V.O., se proponen plantearse como una compleción a la M.C.
Existen muchos tipos de V.O., es decir, de teorías que, incorporando V.O., se proponen plantearse como una compleción a la M.C.
-Por supuesto son posibles muchas clasificaciones distintas, entre ellas:
-Nota previa: en lo siguiente, representamos las V.O. por y el valor medido del observable A en el sistema individual o microestado
, esto es, el resultado de la medida, por
.
1. V.O. contextuales y no-contextuales:
1.a) V.O. no-contextuales
-Los teoremas tipo von Neumann (i.e.: von Neumann, Jauch y Piron, Gleason, etc.) definen por sí mismos un tipo de teorías de V.O.: aquéllas a las que les son aplicables.
-En concreto, definimos las teorías de V.O. no-contextuales, excluidas por estos teoremas, como aquéllas que satisfacen sus hipótesis:
1) Dados dos observables ,
y dos constantes
,
, siendo
, entonces
, donde
representa el valor esperado del operador (autoadjunto)
medido en el microestado
.
2) El valor medido de un observable en un microestado
,
, no depende del contexto en que se realice la correspondiente medida. Es decir, es independiente del tipo de aparato, o montaje experimental concreto, con que se mida; por ejemplo, es independiente de cuáles otras medidas (¡compatibles!) se realicen simultáneamente.
-Una precisión: en sentido estricto, una teoría que incorpora V.O. es no-contextual cuando, dados dos observables (o funciones de ellos) cualesquiera,
y
, es posible definir formalmente una distribución conjunta de densidad de probabilidad de resultados de las medidas sobre el estado cuántico en cuestión (ver ref. [SEL-88], pp. 373ss.).
-En marco EPR, la «simultánea realidad» de dos variables implica la existencia de una distribución conjunta de densidad de probabilidad.
–Varios teoremas de imposibilidad excluyen las V.O. no-contextuales.
1.b) V.O. contextuales
-Una teoría de V.O. es contextual cuando el valor medido de un observable depende del «contexto» C de la medida:
-Toda V.O. que no es contextual es no-contextual, y viceversa.
-En una teoría de V.O. contextuales, el resultado de una medida puede depender no sólo del estado del sistema en que se mide, sino también de la disposición completa del aparato o dispositivo experimental; por ejemplo, de qué otros observables se decida medir también.
-Las V.O. contextuales no están excluidas por ningún teorema matemático.
–El teorema de Bell-Kochen-Specker demuestra la contextualidad de los (algunos) observables cuánticos.
2. V.O. locales y no-locales:
2.a) V.O. locales
![]() Se enuncia un principio de acción local ([GAL-89], vol. I, p. 459):
Se enuncia un principio de acción local ([GAL-89], vol. I, p. 459):
Principio de acción local: «Las condiciones físicas reales de subsistemas aislados, espacialmente separados, son independientes».
-Las V.O. locales se introducen con la meta de satisfacer este principio, y la exigencia que conllevan, matemáticamente, es que el valor esperado de un observable de correlación en un estado del sistema formado por dos subsistemas A y B, espacialmente separados, sin interacción, ha de aparecer como promedio estadístico, sobre los microestados, de los productos de los valores individuales en tales microestados, y cada uno de estos valores individuales (y aquí entra la localidad) dependerá exclusivamente del aparato que sirva para medir el observable individual correspondiente y de las V.O. del microestado, pero no de lo que se haga sobre el otro subsistema (cf. [GAL-89], vol. I, p. 463).
-En esta clasificación asumimos que una V.O. es local cuando bien es no-contextual, bien es contextual y el contexto correspondiente no contiene elementos pertenecientes a regiones separadas EPR (separabilidad einsteiniana), de forma que el contexto puede influir en los resultados de las medidas sin que se involucren en modo alguno «acciones a distancia superlumínicas» (v>c).
–Los teoremas tipo Bell excluyen las V.O. locales (esto es, no son equivalentes, predictivamente, con la MC, y parece que tampoco con los experimentos realizados).
Resulta «sensato» (al menos para la mayoría…) que una V.O. no-contextual haya de ser necesariamente local. Y ello porque, al ser no-contextual, las distribuciones de probabilidad para las medidas dependen sólo, por así decirlo, de lo interno al sistema sobre el que se mide, esto es, del estado de lo medido, y no del contexto o disposición global del experimento.
-Asumimos por definición, pues, que toda V.O. que es no-contextual es local.
Si no-contextualidad implica localidad, se deriva (regla lógica) que no-localidad implica contextualidad.
-Obsérvese que, con las definiciones hechas aquí (¡no son universales: varían con los autores!) las V.O. locales pueden ser bien no-contextuales, bien contextuales, siempre que el contexto no incluya regiones separadas.
2.b) V.O. no-locales
-Una V.O. es no-local cuando no es local (y viceversa).
–Las V.O. no-locales no están excluidas por ningún resultado matemático similar a los históricos teoremas que excluyeron a las variables no-contextuales haciendo uso del propio formalismo matemático de la Mecánica Cuántica.
–Las V.O. no-locales conllevan en general incompatibilidad con la Relatividad.
-Las V.O. contextuales pueden ser locales (entonces el contexto no puede contener regiones separadas) o no-locales.
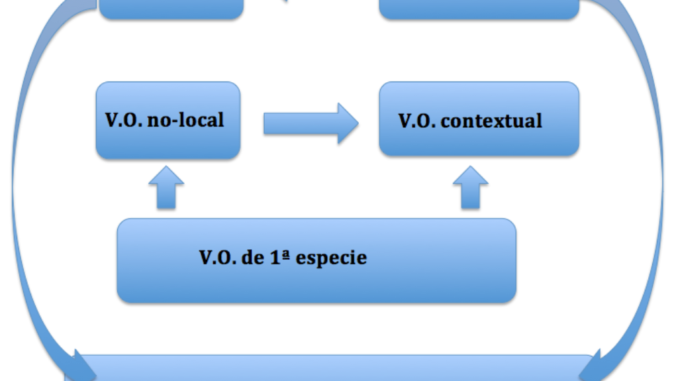
-Relaciones:
V.O. no-contextual V.O. local
V.O. no-local V.O. contextual
3. V.O. de primera y de segunda especie:
3.a) V.O. de primera especie
-Son aquéllas que se desarrollan con el requisito de permitir reproducir todas las predicciones estocásticas de la M.C.
-Son, necesariamente, V.O. contextuales no-locales.
-Ejemplo: las V.O. de la teoría cuántica de Bohm (¡cuidado: son de primera especie en cuanto a la mecánica cuántica no relativista!).
-Nota: pero, obviamente, el que una teoría de V.O. utilice V.O. de tipo contextual no-local no la convierte en predictivamente equivalente a la M.C. Es decir, no toda V.O. contextual no-local ha de ser de primera especie.
3.b) V.O. de segunda especie
-Son variables incompatibles con la M.C., es decir, tales que las correspondientes teorías llevan a predicciones diferentes de las de la M.C. en determinadas situaciones experimentales. Se incluyen aquí todas las V.O. no-contextuales; todas las V.O. locales; algunas contextuales y algunas no-locales.
-Tanto las V.O. locales como las no-contextuales, son V.O. de 2ª especie.
![]() El teorema de Bell vendría a establecer que las V.O. locales, todas, son inconsistentes con la M.C.
El teorema de Bell vendría a establecer que las V.O. locales, todas, son inconsistentes con la M.C.
![]() El avance que supuso el teorema de Bell fue añadir las VO. locales contextuales a la lista de inconsistentes con la M.C., es decir, declararlas V.O. de segunda especie. Su repercusión fue enorme, porque hizo ver que es la conjunción realismo + localidad (= realidad separable, no confundir con la causalidad relativista: consultar el apartado sobre terminología EPR) lo que conlleva la inconsistencia con la Mecánica cuántica.
El avance que supuso el teorema de Bell fue añadir las VO. locales contextuales a la lista de inconsistentes con la M.C., es decir, declararlas V.O. de segunda especie. Su repercusión fue enorme, porque hizo ver que es la conjunción realismo + localidad (= realidad separable, no confundir con la causalidad relativista: consultar el apartado sobre terminología EPR) lo que conlleva la inconsistencia con la Mecánica cuántica.
![]() Bell clarificó que lo que los teoremas de von Neumann (1932), Gleason y similares, anteriores al suyo de 1964 sobre VO locales, habían establecido era que: todas las V.O. no-contextuales (que son todas locales por lo dicho) son inconsistentes con la M.C.
Bell clarificó que lo que los teoremas de von Neumann (1932), Gleason y similares, anteriores al suyo de 1964 sobre VO locales, habían establecido era que: todas las V.O. no-contextuales (que son todas locales por lo dicho) son inconsistentes con la M.C.
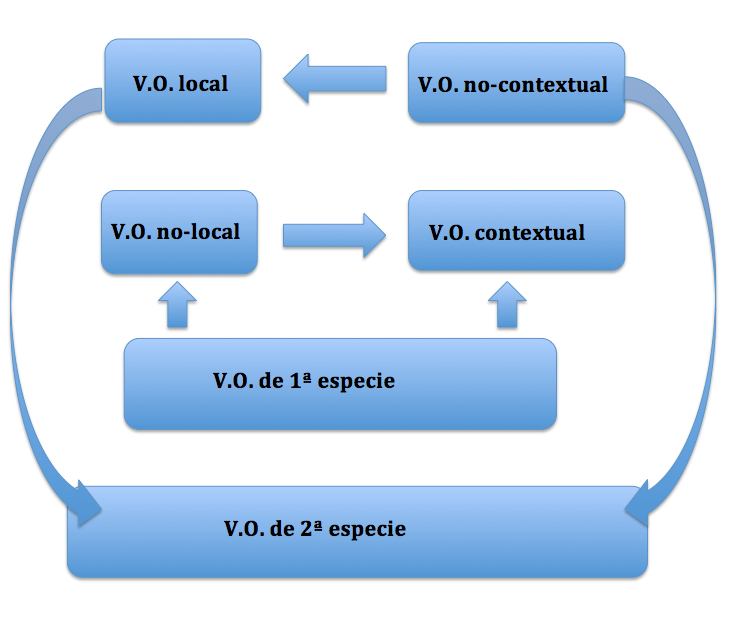
Diagrama de conexiones lógicas entre VO
![]() Esquema en que se muestran las relaciones lógicas entre los distintos tipos de V.O., según se han definido antes:
Esquema en que se muestran las relaciones lógicas entre los distintos tipos de V.O., según se han definido antes:
Bibliografía
- [BEL-90] Bell, J.S.; Lo decible y lo indecible en mecánica cuántica, Alianza Univ., 1990.
- [ESP-76] Espagnat, B.d’; Conceptual Foundations of Quantum Mechanics, Benjamin, 1976.
- [GAL-89] Galindo, A. y Pascual, P.; Mecánica Cuántica, Eudema, Madrid, 1989.
- [ICA-91] Icaza, J.J.; La construcción de la Mecánica Cuántica, Univ. del País Vasco, Bilbao, 1991.
- [JAM-74] Jammer, M.; The philosophy of Quantum Mechanics,Wiley, 1974.
- [NEU-91] Neumann, J. von; Fundamentos matemáticos de la Mecánica Cuántica, Consejo Superior de Investigaciones Científicas, Madrid, 1991.
- [SEL-88] Selleri, F., ed.; Quantum Mechanics Versus Local Realism. The Einstein-Podolsky-Rosen Paradox, Plenum, New York, 1988.
- [WHE-83] Wheeler, J.A. y Zurek,W.H., eds.; Quantum Theory and measurement, Princenton Univ., Princenton, 1983.
Dejar una contestacion