El experimento de Stern-Gerlach y el espín

Resultados del experimento de Stern y Gerlach en 1922 — Postal enviada por W. Gerlach a N. Bohr, con fecha 8 de febrero de 1922, mostrando el desdoblamiento observado en su experimento. El texto que incluyó fue: «Adjunto la prueba experimental de la cuantización espacial. Le felicitamos por la confirmación experimental de su teoría.» (Fuente: https://pubs.aip.org/physicstoday/article/56/12/53/632269/Stern-and-Gerlach-How-a-Bad-Cigar-Helped-Reorient).

El experimento de Stern-Gerlach

El experimento de Stern-Gerlach fue realizado en 1922 por O. Stern y W. Gerlach; su explicación teórica correcta no se alcanzaría hasta 1927, dos años más tarde de la introducción del espín electrónico, concepto indispensable postulado en 1925 por S. Goudmit y G.E. Uhlenbeck para explicar el efecto Zeeman anómalo (aunque la primicia de la concepción, por meses, se deba a R. Kronig, quien sin embargo desistiría de publicar su idea por la desfavorable opinión inicial hacia el concepto expresada por un muy influyente W. Pauli).
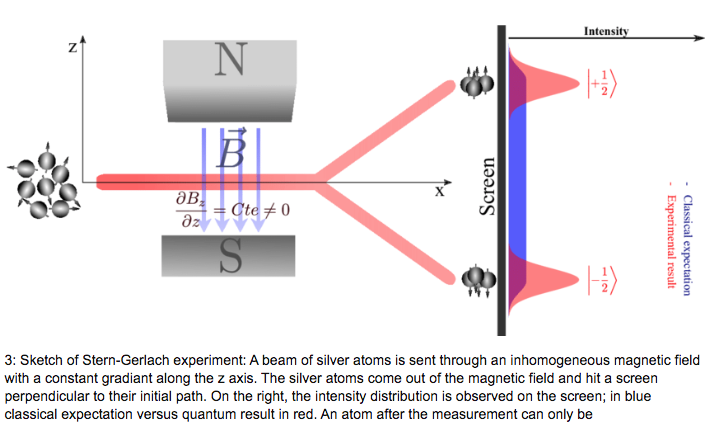
Un haz de átomos de Plata atraviesa un campo magnético exterior inhomogéneo o no uniforme, según se ilustra en la figura adjunta; elegimos el eje vertical $OZ$ según la dirección espacial entre los dos polos del imán y 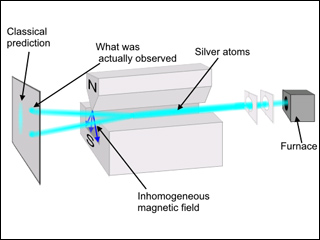el haz se dirige según una dirección de propagación, el eje $OY$ , perpendicular a la dirección de variación del campo o gradiente de $\vec{B}$ . Las razones de esta configuración experimental que diseñaron Stern y Gerlach estaban claras:
a) Átomos neutros, y no de carga $q$ , para evitar la aparición de las fuerzas de Lorentz $\vec{F_{Lo}}=q \ (\vec{v} \times \vec{B})$ , siendo v la velocidad de entrada al imán de las partículas, ya que estas fuerzas habrían producido unas desviaciones en las trayectorias atómicas, las cuales, superpuestas y de mayor magnitud que las producidas por los momentos magnéticos atómicos, relacionados con los momentos angulares, habrían impedido estudiar estos últimos. Y es que unos átomos cargados habrían salido disparados hacia los lados de forma muy caótica, y/o habrían seguido trayectorias curvas muy pronunciadas, ocultando por completo la pequeña desviación que se quería medir, para confirmar o no la postulada cuantización espacial del momento angular orbital $\vec{L}$ (modelo de Bohr-Sommerfeld).
b) Átomos de Plata porque, al tener la plata 47 electrones, Z=47, su configuración electrónica distribuye 46 de ellos en capas cerradas, de modo que los momentos magnéticos se cancelan entre sí, resultando un momento magnético neto nulo. Y el electrón número 47 se dispone solitario en el orbital más externo, de modo que todo el momento magnético $\vec{\mu}$ del átomo de plata depende exclusivamente del momento angular de ese solo electrón. Es obvio que esta situación era idónea para producir un resultado más «limpio» de interpretar.
c) Campo magnético $\vec{B}$ inhomogéneo, variando según una dirección vertical dirigida entre los polos del imán empleado, porque si el campo fuese uniforme, la fuerza resultante sobre el momento magnético atómico $\vec{\mu}$ , $\vec{F_{\mu}}= - \nabla V$ , donde $V$ representa la energía potencial, $V= -\vec{\mu} \cdot \vec{B}$ , provocaría sólo un movimiento de precesión (Larmor) alrededor de la dirección del campo magnético $\vec{B}$ , sin desplazamiento neto del dipolo hacia la región de mayor intensidad del campo (el gradiente en un campo magnético homogéneo es igual a cero). En cambio, en el seno del campo inhomogéneo la fuerza neta sobre el átomo es $F_z=\mu_z \frac{\partial B_z}{\partial z}$ , siendo $\mu_z$ la componente del momento magnético según la dirección del gradiente del campo.
d) Trayectoria de incidencia perpendicular al gradiente del campo magnético, con el fin de maximizar las deflexiones laterales d, que a la salida del imán serán (para las dos desviaciones simétricas y opuestas observadas): $|d|=\frac{1}{2}a_zt^2=\frac{1}{2} (F_z/m_e) (b/v_y)^2$ , donde a es la aceleración , t el tiempo de tránsito en el interior del imán, b es la extensión de dicha zona de tránsito, donde actúa el campo magnético; $v_y$ la componente según OY de la velocidad, que corresponde a un movimiento sin aceleración en el eje OY, $y(t)=v_yt$ .
En el montaje final del experimento, un haz de átomos de plata producidos por efusión del vapor metálico producido en un horno calentado a 1000 °C era colimado por dos rendijas estrechas de unos 0.03 mm y se le hacía atravesar una bobina magnética de 3.5 cm de longitud, con un campo magnético de una intensidad máxima de 0.1 tesla y un gradiente máximo de unos 10 teslas/centímetro. La desviación de los haces atómicos conseguida era tan sólo de 0.01 mm, y es interesante mencionar que, según los diversos relatos sobre este famoso experimento, el instrumento original solía estropearse unas pocas horas después de iniciarse el experimento, por lo que tan sólo una fina capa de átomos de plata eran depositados en la placa a impresionar. Lentamente, mientras Stern y Gerlach, en medio de un denso humo procedente de cigarros de alto contenido en azufre, exploraban la placa receptora de los impactos, sobre esta empezaron a aparecer las claras manchas que mostraban el paso del haz.
En efecto, según la teoría electromagnética, cada fuente de campo magnético (en este caso, el electrón externo, una partícula de carga $e$ , en giro orbital clásico en torno a las capas cerradas internas) posee una propiedad vectorial denominada momento magnético (dipolar), $\vec{\mu}$ , que clásicamente es proporcional a su momento angular, $\vec{\mu}= -\frac{|e|}{2m_e}\vec{L}=-\mu_B \frac{\vec{L}}{\hbar}$ , donde $\mu_B=\frac{|e|\hbar}{2m_e}=9,27408 \times10^{-24}\,JT^{-1}$ es una constante, denominada «el magnetón de Bohr» (unidades Julio/Tesla). El momento angular (orbital) atómico $\vec{L}$ depende en general de los electrones de valencia o electrones en la capa más externa de un átomo; por ejemplo, en el átomo de Plata las capas electrónicas internas están todas llenas, al máximo de su capacidad, de modo que la suma vectorial de todos los momentos conduce a que es el solo electrón de valencia el responsable de ese momento. En los modelos pre-cuánticos de la época del experimento, 1922, ese solitario electrón era supuesto en órbita en torno al núcleo del átomo y el conjunto de capas electrónicas internas llenas, siendo él solo el responsable del momento magnético, al aportar los restantes electrones una contribución neta nula al momento angular. Es decir, el electrón de valencia, como cualquier carga eléctrica que gira en una órbita, funcionaría como un minúsculo electroimán, generando un pequeño campo magnético.
Así pues, si consideramos (¡descripción clásica!) el electrón más externo girando en una órbita circular de radio $r$ , el momento magnético dipolar es normal al plano de la corriente así constituida, de intensidad $I=\frac{|e|v}{2\pi r}$ , de forma que:
$\vec{\mu}=Id\vec{S}$ ,
donde $|\vec{S}|=\pi r^2$
y
$\mu=-\frac{|e|v\pi r^2}{2\pi r}=-\frac{|e|m_evr}{2m_e}=-\frac{|e|}{2m_e}L$ ,
$L=|\vec{L}| \; , \; \vec{L}=m_e \ \vec{r} \times \vec{v}$ ,
según se representa en la siguiente figura (con notación $m=m_e \ , \ A=S$ ):

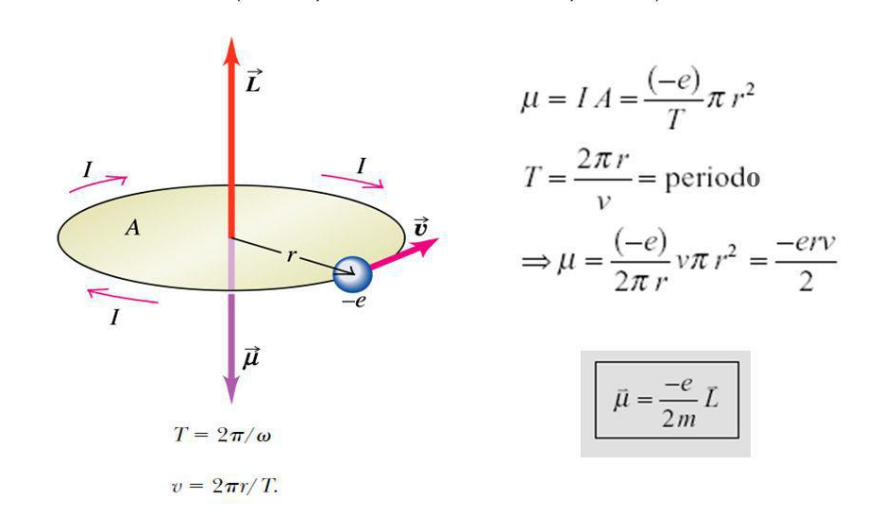
Obsérvese que el momento magnético dipolar tiene igual dirección que el momento angular orbital, y sentido opuesto.
En el seno del campo magnético, la energía de interacción entre el momento magnético y el campo viene dada por $V=-\vec{\mu} \cdot \vec{B}$ ; la deflexión que experimentará cada átomo dependerá de la orientación relativa entre su momento magnético y la dirección del campo inhomogéneo entre los bornes del imán.
Según lo expuesto, el efecto del campo magnético no uniforme sobre cada átomo es desviarlo de su trayectoria rectilínea inicial, y la desviación depende de la orientación específica del vector momento magnético (en particular, por la disposición experimental descrita, de su tercera componente $\mu_z$ ). Al entrar cada átomo de Plata en la zona del campo magnético $\vec{B}$ , su momento magnético $\vec{\mu}$ estará orientado al azar, siendo todas las orientaciones posibles según la teoría clásica (sin cuantización espacial alguna). El campo magnético provocaría entonces que los átomos fueran desviados de un modo aleatorio, dependiendo el grado de deflexión de cada átomo particular del ángulo inicial entre su correspondiente vector (orientación aleatoria) y el campo magnético (líneas del campo dirigidas desde el polo norte hacia el sur y no paralelas, véase la figura). Por lo tanto, algunas partículas serían desviadas fuertemente, otras de manera más débil, etc., debiendo observarse sobre la pantalla situada a la salida, según una teoría estrictamente clásica, una zona continua cubierta de impactos. Y midiendo la desviación individual (a partir de dónde impacta cada átomo), se podría determinar directamente la componente z de su momento magnético.
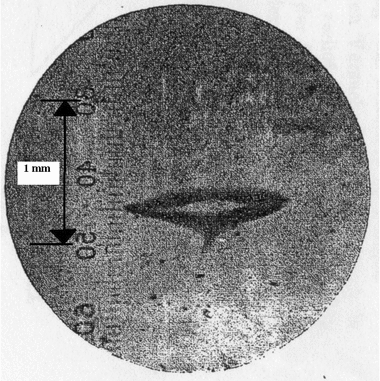
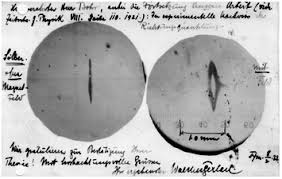
Pero lo que encontraron Stern y Gerlach es lo que se indica en las siguientes figuras:
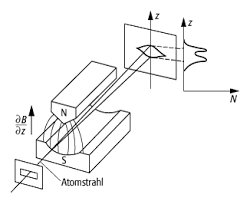
Resultados del experimento de Stern-Gerlach.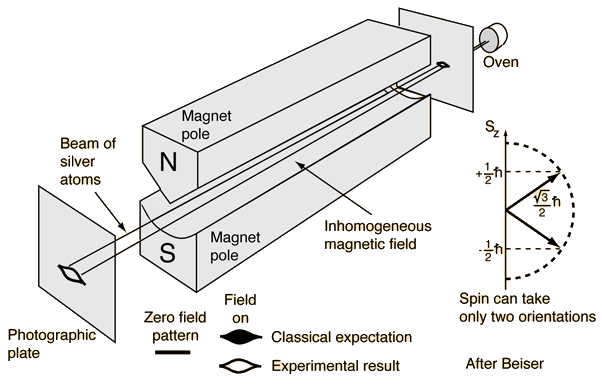
Es decir, el resultado del experimento que encontraron Stern y Gerlach indicaba que sólo había dos ángulos de deflexión, o sea, lo que observaron es que todas las partículas
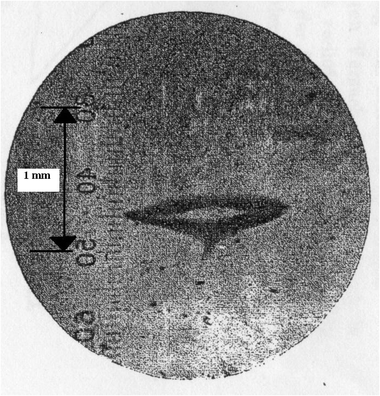
W. Gerlach, O. Stern, «Der experimentelle Nachweis der Richtungsquantelung im Magnetfeld»; Zeitschrift für Physik A, Hadrons and Nuclei, Vol. 9, No. 1, (1922) 349-352.

fueron desviadas o bien hacia arriba o bien hacia abajo, y ambos grupos con la misma intensidad, dibujando por la simetría del problema una figura en forma de labios abiertos, sin que ningún átomo impactara en la zona central. El experimento sugería que los átomos de Plata sólo poseían dos orientaciones particulares de su momento magnético y, por tanto, de su momento angular, un resultado inexplicable para la física clásica, que predecía una sola y amplia mancha continua.
Los modelos de cuantización primitivos, como el que había introducido Sommerfeld en 1916 generalizando el de Bohr (modelo de Bohr-Sommerfeld-Debye), conducían a una predicción de resultados distinta a la clásica, y como en ese momento histórico, 2022, se asignaba un momento angular incorrecto a los átomos de Ag utilizados, en concreto un momento angular unidad, $l=1$ ( $\hbar$ ), el experimento pareció justificar la prediccción de cuantización espacial introducida por esos modelos. Aunque para ello hubo que aceptar la suposición, aceptada por Bohr entre dudas, de que para el valor $l=1$ sólo podrían tenerse los dos valores $m=\pm 1$ para el correspondiente número cuántico, excluyendo como imposible el valor nulo.
El hecho histórico es que habría que esperar a la conjunción de dos nuevos avances en la Física, uno, la postulación en 1925 por S. Goudmit y G.E. Uhlenbeck del espín electrónico, y dos, el que en 1927 R. Fraser estableciera que el estado fundamental de los átomos neutros como la plata y el sodio, entre otros, era cero, para alcanzar finalmente la correcta justificación teórica del experimento de Stern y Gerlach. En efecto: una vez incorporado el valor $\frac{1}{2}$ para el momento angular intrínseco del electrón, o espín electrónico, a partir de los dos valores de su tercera componente $\pm \frac{1}{2}$ , y fijado el valor nulo para el momento angular orbital, $l=0$ , se justificaría la presencia de las dos manchas observadas (convirtiendo pues en errónea la anterior fundamentación teórica, algo que ignoran todavía en muchas fuentes de información actuales, incluida la AI, que fijan en 1925, con la incorporación del espín, la explicación completa del experimento).
En efecto: en el modelo precuántico de Bohr-Sommerfel se introducían unas cuantizaciones para el momento angular orbital y su tercera componente según $L = n_{\psi} \hbar$ y $L_z = m \hbar$ ; el número cuántico $n_{\psi}$ tomaba valores enteros y, para cada valor suyo, el número cuántico $m$ podía tomar los valores $m=-n_{\psi},-n_{\psi}+1,-n_{\psi}+2, \cdots ,-1,0,+1,+2,\cdots ,n_{\psi}-2,n_{\psi}-1,n_{\psi}$ . Conforme con estos modelos, debería observarse sobre la pantalla, para cada valor $l$ , un número de manchas o zonas de localización de impactos compatible con un número impar $2 n_{\psi}+ 1$ de posibilidades para las desviaciones de los átomos. El porqué de esas dos únicas manchas, y no las tres correspondientes a los sendos valores m =0, ±1 (l=1) en el experimento realizado se justificó pues bajo las erróneas suposiciones de que, uno, el momento angular orbital del átomo de Ag era $\hbar$ , siguiendo el modelo de Bohr, y dos, aunque con muchas dudas, el mismo Bohr acabó por decidir que el valor m=0 no se tuviera en cuenta: en el caso m = 0 el electrón se movería en una órbita paralela al campo magnético que define la dirección privilegiada OZ, lo que resultaría inestable. Por tanto, cabía esperar sólo dos orientaciones del momento magnético (a favor y en contra del campo), lo que dejaba sólo dos posibilidades para la cuantización espacial. El resultado del experimento, pues, fue considerado y aceptado como una gran confirmación de los modelos cuánticos primitivos, y su predicción del fenómeno de la cuantización espacial, frente a la física clásica.
Sobre la realización experimental:
El experimento en la web Cienciaes.com: Stern-Gerlach. El experimento que cambió el curso de la Física:
El haz atravesaba entonces un campo magnético inhomogéneo de una décima de Tesla con una variación de diez Teslas por centímetro generado por un imán de tres metros y medio de longitud, antes de chocar con una placa colectora, donde la posición de los átomos de plata depositados indicaría su trayectoria. Y todo esto, al vacío, para evitar que los átomos de plata chocasen contra las moléculas del aire durante su recorrido. Con este montaje, la separación esperada de los haces resultantes en la placa colectora era de sólo 0,2 mm, por lo que los aparatos debían estar alineados con una precisión de 0,01 mm. Por razones técnicas, el experimento nunca llegaba a funcionar más de unas pocas horas seguidas, así que los depósitos de plata recogidos eran extremadamente tenues, invisibles a simple vista. Cuando Gerlach retiró la placa colectora, no vio ni rastro de plata en ella, y se la pasó a Stern, que se la llevó a los ojos para examinarla de cerca. Y entonces, mientras Stern observaba la placa, con su colega mirando por encima de su hombro, ambos se sorprendieron al ver que una sombra negra, la huella del haz de plata, empezaba a hacerse visible gradualmente. ¿Qué estaba ocurriendo? En aquella época, los exiguos sueldos de Stern y Gerlach no les permitían grandes alegrías, así que fumaban unos cigarros baratos con un alto contenido de azufre. El humo del tabaco, al reaccionar con la plata, había formado sulfuro de plata, de color negro azabache. Fue como revelar un negativo fotográfico. En un principio, Stern creyó que el azufre procedía de su propio aliento, pero un experimento realizado por los físicos Bretislav Friedrich y Dudley Herschbach, de la Universidad de Harvard, en febrero de 2002, coincidiendo con la inauguración de un nuevo centro de física experimental dedicado a Stern y Gerlach en la Universidad de Francfort, demostró que el aliento no era suficiente; sólo el humo del cigarro podía ennegrecer y hacer visible la plata.
La Historia del experimento en Physics Today: B. Friedrich and D. Herschbach; Physics Today 56 (12) 53–59 (2003); Stern and Gerlach: How a bad cigar helped Reorient Atomic Physics:
In view of the interest aroused by the SGE in 1922, we would expect that the postulation of electron spin in 1925 should very soon have led to a reinterpretation of the SGE splitting as really due to spin. However, the earliest attribution of the splitting to spin that we have found did not appear until 1927, when Ronald Fraser noted that the ground-state orbital angular momentum and associated magnetic moments of silver, hydrogen, and sodium are zero. Practically all current textbooks describe the Stern–Gerlach splitting as demonstrating electron spin, without pointing out that the intrepid experimenters had no idea it was spin that they had discovered.
J. Santoro, 100 años del experimento de Stern-Gerlach:
Stern y Gerlach eligieron la plata suponiendo que l = 1. De los tres valores posibles de m eliminaron el caso m = 0 siguiendo la propuesta de Bohr. Supusieron que el impulso angular total era $\hbar$ . Consideraron que el impulso angular estaba orientado por completo a favor (m = 1) o en contra (m = -1) del campo magnético…. El experimento Stern-Gerlach se había diseñado para dilucidar “si la concepción teórica cuántica o la clásica es la correcta”. El experimento demostraba fuera de toda duda la existencia de una cuantización direccional. Eliminaba, por tanto, el comportamiento clásico. Sin embargo, la descripción cuántica estaba basada en una serie de hipótesis equivocadas que, de un modo totalmente afortunado, derivaban en una predicción correcta del resultado esperado. Mientras que el experimento proporcionaba evidencias concluyentes contra la teoría clásica, la supuesta validación de la vieja teoría cuántica era incorrecta, puesto que gran parte de sus hipótesis lo eran.
B. Friedrichs, «A Century Ago the Stern–Gerlach Experiment Ruled Unequivocally in Favor of Quantum Mechanics» (https://doi.org/10.1002/ijch.202300047), hace este relato sobre la dificultad del experimento:
Wilhelm Schütz (1900–1972), who was in 1922 Gerlach’s Ph.D. student, described the difficulties of the SGE as well as the final triumph on 8 February 1922 as follows:
The old apparatus had only yielded a broadening of the silver beam [deposit on the glass plate] of the expected magnitude … due to the inhomogeneous magnetic field. A major improvement of the apparatus with the aim to further increase its resolution was [therefore] necessary. During this rebuilding period, Stern moved to Rostock to assume a Professorship for Theoretical Physics there. He would show up in Frankfurt every now and then (during Christmas 1921 and Easter 1922) for discussions and to measure the inhomogeneity of the magnetic field… Soon came the time when I was able to enter the holy premises of the laboratory and take a look at the pumps, when [the technician Mr. Adolf] Schmidt was not on duty and Prof. Gerlach had to sleep once in a while… Anyone who has not been through it cannot at all imagine how great were the difficulties with an oven to heat the silver up to about 1300 K within an apparatus which could not be heated in its entirety [the seals would melt] and where a vacuum of $10^5$ Torr had to be produced and maintained for several hours. The cooling was done with solid carbon dioxide and acetone or with liquid air. The pumping speed of the Gaede mercury backing pumps and the Volmer mercury diffusion pumps was ridiculously low compared with the performance of modern pumps. And then their fragility; the pumps were made of glass and quite often they broke, either from the thrust of boiling mercury… or from the dripping of condensed water vapor. In that case the effort of several days of pumping, required during the warming up and heating of the oven, was lost. Also, one could be by no means certain that the oven would not burn through during the four- to eight-hour exposure time. Then both the pumping and the heating of the oven had to be started from scratch. It was a Sisyphus-like labor and the main load of responsibility lay on the broad shoulders of Prof. Gerlach. In particular, W. Gerlach would take over the night shifts. He would get in at about 9 p.m. equipped with a pile of reprints and books. During the night he then read the proofs and reviews, wrote papers, prepared lectures, drank plenty of cocoa or tea and smoked a lot. When I arrived the next day at the institute, heard the intimately familiar noise of the running pumps, and found Gerlach still in the lab, it was a good sign: nothing broke during the night.
El resultado experimental observado carecería de interpretación correcta teórica, en términos del espín electrónico, un momento angular intrínseco sin análogo clásico postulado por S. Goudmit y G.E. Uhlenbeck en 1925 para explicar el efecto Zeeman anómalo (desdoblamiento de niveles atómicos en campos magnéticos débiles), hasta años más tarde, cuando R. Fraser estableciera la simetría esférica (estado S) del estado fundamental de los átomos neutros de hidrógeno, sodio y plata. Por ejemplo, en el átomo neutro de plata, el electrón de valencia externo se encuentra en un orbital $s$ , con momento angular orbital cero, lo que da lugar a un estado fundamental $2S_{\frac{1}{2}}$ (configuración electrónica: $[Kr] 4d^{10}5s^{1}$ ), cuyo momento orbital total es nulo. Dos años después de su introducción, la nueva variable cuántica del espín fue desarrollada y dotada de rigor matemático por W. Pauli en 1927, siendo incorporada por Dirac en 1928 a su ecuación mecánico-cuántica relativista para el electrón.
Las palabras de Wolfgang Pauli al conocer el resultado del experimento fueron (cf. How a bad cigar helped Reorient Atomic Physics):
As a beginning graduate student back in 1923, I … hoped with ingenuity and inventiveness I could find ways to fit the atomic phenomena into some kind of mechanical system…. My hope to [do that] died when I read about the Stern–Gerlach experiment…. The results were astounding, although they were hinted at by quantum theory…. This convinced me once and for all that an ingenious classical mechanism was out and that we had to face the fact that the quantum phenomena required a completely new orientation.

Cuantización espacial

El fenómeno de la cuantización espacial, que ya vimos como aparecía en el modelo atómico de Sommerfeld de 1916, se interpretó estableciendo que la orientación del plano de las órbitas permitidas (un concepto precuántico) respecto a una dirección dada no puede ser arbitrario, sino que su normal (esto es, la dirección de $\vec{L}$ ) debe formar con el eje $OZ$ (en general, con cualquier dirección prefijada) un ángulo $\phi$ dado por $cos\phi=\frac{L_z}{L}=\frac{m}{n_\psi}$ . Puesto que el espacio es isótropo, esta cuantización que surge en el modelo carece de sentido físico hasta que no se marque experimentalmente una dirección en el espacio, por ejemplo aplicando un campo magnético.
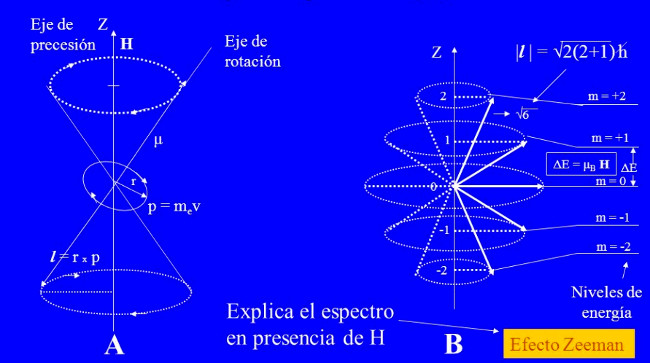
La cuantización espacial (ya discutida en el apartado modelos atómicos primitivos y con la que se logró explicar el efecto Zeeman «normal» o clásico: los tripletes de Lorentz); imagen por Angélica Oquendo en SlidePlayer; H representa el campo magnético exterior.
La predicción del fenómeno de la cuantización espacial, por tanto, habría quedado supuestamente confirmada por el experimento en 1922 de O. Stern y W. Gerlach, vía la medida de momentos magnéticos atómicos, aunque en realidad sólo sería justificada teóricamente años después, cuando se combinarían la aplicación del concepto de espín, un momento angular intrínseco sin análogo clásico postulado en 1925 por S. Goudmit y G.E. Uhlenbeck para explicar el efecto Zeeman anómalo, y el momento angular orbital correcto (nulo) de los átomos neutros de plata.
En efecto: el resultado del experimento de Stern y Gerlach indicaba la presencia de sólo algunos ángulos de deflexión, en conformidad con la predicción teórica de un fenómeno de cuantización espacial, y el que sólo aparecieran dos valores de deflexión se casaba con la predicción de los modelos de cuantización primitivos: el experimento sugería que los átomos de plata, que eran supuestos con momento angular orbital l=1, eliminado el valor m=0, sólo poseían dos orientaciones particulares de su momento magnético, un resultado inexplicable para la Física Clásica (predicción de mancha continua). Pero el hecho es que la observación de sólo dos manchas se haría pronto también incompatible e injustificable para los modelos de cuantización primitivos, como el que había introducido Sommerfeld en 1916, ya que R. Fraser demostró posteriormente que para átomos neutros como los de plata, hidrógeno, sodio… en realidad en el estado fundamental debía asociarse con un momento magnético nulo, ya que les correspondía un valor del número cuántico l=0. Y la única explicación teórica justificativa pasó entonces a basarse en la hipótesis del espín electrónico: es el electrón de valencia, con s=1/2, el responsable de todo el momento magnético del átomo y de las dos posibles orientaciones ( $m_s= \pm \frac{1}{2}$ ) observadas. Como se comenta en todos los artículos antes citados, en realidad Stern y Gerlach no fueron conscientes en su momento de que lo que su experimento había establecido es la manifestación de la nueva propiedad cuántica del espín de las partículas, y su cuantización espacial. Lo cual es obvio: ¡todavía no había sido formulado!
Explicación: el espín electrónico está cuantizado, pudiendo arrojar como resultado de su medida (sobre un estado arbitrario o no preparado con una medida previa filtrante) según cualquier dirección (su proyección) sólo los dos valores $\pm \frac{\hbar}{2}$ , lo que provoca en consecuencia dos únicas sendas deflexiones: las partículas con componente de espín según esa dirección, con valor $+\frac{\hbar}{2}$ , son desviadas hacia arriba, y las partículas con componente opuesta, valor $-\frac{\hbar}{2}$ , son desviadas en el sentido contrario. Es decir, el momento magnético de los diferentes átomos sólo podía tomar, en las condiciones del experimento, dos valores, ya que, en términos del espín $\vec{S}$ , el momento magnético tiene el valor $\vec{\mu}=-\mu_B g_s \frac{\vec{S}}{\hbar}$ , donde $\mu_B$ es el magnetón de Bohr; $g_s$ es el «factor giromagnético «g» del electrón, o factor g de Landé, una constante de valor $g_s=2,002319$ para el espín y g=1 para el momento angular orbital; $\vec{S}$ es el espín o momento angular intrínseco; el correspondiente hamiltoniano de interacción tiene la expresión $H_B=-\vec{\mu}\cdot \vec{B}$ ). Repárese en que se trata del caso en que $\vec{L}=0$ ; se aplica la cuantización $L=\hbar \sqrt{l(l+1)}$ , $l=0, \pm 1, \pm 2, \cdots , \pm l$ , y en este caso de momento angular orbital nulo, sólo se tiene $l=0$ . Luego todo el momento magnético dipolar procede del espín electrónico, teniéndose: $S=\hbar \sqrt{s(s+1)}$ ; $s=\frac{1}{2}$ ; $m_s= +\frac{1}{2}\, ,-\frac{1}{2}$ ( $m_s$ es el número cuántico de tercera componente de espín).

El espín electrónico

Como se comentó anteriormente, el concepto de espín electrónico surgió en el contexto experimental del denominado efecto Zeeman «anómalo», o desdoblamientos de las líneas espectrales observados al situar los átomos en el seno de campos magnéticos de intensidades débiles. En este caso, se producen desdoblamientos de naturaleza diferente (efecto Paschen-Back para campos medios y Zeeman anómalo para campos débiles, éste descubierto por T. Preston) a los correspondientes a campos intensos, o efecto Zeeman normal, el único que logró ser explicado por la teoría clásica y los modelos pre-cuánticos como el de Sommerfeld.
En el efecto Zeeman anómalo, cada línea espectral se desdobla de una manera que sólo encontrarían justificación en la teoría plenamente cuántica moderna, en que se incorpora el espín electrónico, nueva magnitud cuántica sin análogo clásico y para cuyo descubrimiento la experimentación relacionada con los distintos efectos Zeeman fue decisiva. En 1925, Uhlenbeck y Goudmit postularían el espín o momento angular intrínseco, cuya incorporación al Hamiltoniano de interacción del momento magnético atómico con el campo magnético permitió por fin explicar teóricamente las correspondientes observaciones experimentales. Históricamente, parece que ya en 1921 A. Compton había sugerido que el electrón podría tener un momento magnético intrínseco, y que también R. Kronig, en el mismo 1925, habría especulado con ello, pero ninguno de ellos desarrolló el concepto (en el segundo caso, por decisión de W. Pauli). La bibliografía señala que cuando Uhlenbeck y Goudmit, sin conexión con Kronig, presentaron el artículo para su revisión previa a la publicación a Ehrenfest, Lorentz se mostró muy crítico. El cálculo mostraba que un electrón, concebido a la clásica como una diminuta bola en rotación, superaría la velocidad de la luz en su límite exterior, marcado por la estimación contemporánea de su radio… Ehrenfest, pese a ello, lo envió, porque, les dijo a los autores, «sois lo suficientemente jóvenes como para poder decir algunas tonterías».
El espín de un electrón es una magnitud vectorial $\vec{S}$ , cuyo módulo vale $\hbar\sqrt{s(s+1)}=\hbar \frac{\sqrt{3}}{2}$ , ya que el número cuántico de espín $s$ tiene el valor $s=\frac{1}{2}$ para el electrón; sus dimensiones son las de un momento angular (es decir, momento lineal por distancia); es usual medirlo en unidades de la constante de Dirac o $h$ barrada, $\hbar=\frac{h}{2\pi}$ . Presenta un fenómeno de cuantización espacial, consistente en que, fijada una dirección arbitraria $\vec{d}$ en el espacio, que suele tomarse como eje $OZ$ , la medida de su proyección sobre esa dirección, o componente $S_z$ , sólo produce dos resultados:

Magnitud $+\frac{\hbar}{2}$ , apuntando en el sentido creciente del eje $OZ$ ; este resultado por convención se refiere como «hacia arriba» y se nota como $\uparrow$ . Se corresponde con las orientaciones del vector $\vec{S}$ con origen en $O$ y situadas sobre la superficie de un cono con vértice también en $O$ y eje a lo largo de la dirección positiva $OZ$ (según dirección marcada como $\vec{d}$ en la figura siguiente). Algunas de estas posibles orientaciones se muestran dibujadas en la figura adjunta, cono superior.
Resultado análogo, de igual magnitud, pero correspondiente a la proyección apuntando en el sentido decreciente, $-\frac{\hbar}{2}$ , «hacia abajo», $\downarrow$ . En este caso, se corresponde con las orientaciones de $\vec{S}$ con origen en $O$ y sobre la superficie de otro cono similar al anterior, también con vértice $O$ y eje a lo largo de $OZ$ , pero ahora en sentido decreciente: enfrentado al anterior. Corresponde al cono inferior en la figura:

Únicas posibles orientaciones para el espín electrónico respecto a una dirección arbitraria d, marcada como eje OZ; se corresponden con las direcciones con origen en O y sobre la superficie de dos conos enfrentados por su vértice común en O. Todas proporcionan en su proyección sobre un eje OZ una longitud de magnitud $\hbar /2$ , pero una mitad con signo positivo (sentido creciente del eje) y la otra negativo (sentido decreciente); $\hbar$ representa la constante de Planck reducida o constante de Dirac, $\hbar=h/(2\pi)$ (imagen del libro «La realidad cuántica», de RBA ediciones, colección «Un paseo por el cosmos», núm. 32).

Únicas posibles orientaciones para el espín electrónico respecto a una dirección arbitraria d, marcada como eje OZ; se corresponden con las direcciones con origen en O y sobre la superficie de dos conos enfrentados por su vértice común en O. Todas proporcionan en su proyección sobre un eje OZ una longitud de magnitud $\hbar /2$ , pero una mitad con signo positivo (sentido creciente del eje) y la otra negativo (sentido decreciente); $\hbar$ representa la constante de Planck reducida o constante de Dirac, $\hbar=h/(2\pi)$ (imagen del libro «La realidad cuántica», de RBA ediciones, colección «Un paseo por el cosmos», núm. 32).

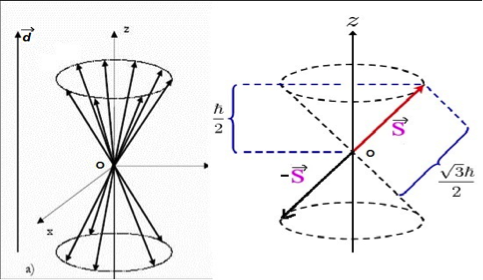
En el formalismo cuántico, el electrón se describe como un «fermión», o partícula con un número cuántico de espín $s$ semi-impar (1/2, 3/2, etc.); en particular, al electrón le corresponde el valor $s=\frac{1}{2}$ .
El postulado del espín electrónico cuantizado permitió explicar ciertos desdoblamientos adicionales observados en algunas líneas espectrales, como los que constituyen el efecto Zeeman anómalo, que se produce al situar átomos en campos magnéticos débiles; también la estructura fina de las líneas espectrales, por la que algunas de ellas, miradas con mayor precisión, resultan estar compuesta por varias líneas muy juntas (un fenómeno cuya comprensión completa requiere espín y teoría relativista).
Además, el espín electrónico resultaría ser la pieza ausente con la que se lograría entender por fin el resultado observado en el experimento Stern-Gerlach: al incorporar el cálculo del momento angular total los espines de todos los electrones del átomo de Plata, añadiéndolos a los momentos angulares orbitales, resultaba que el momento angular total dependía sólo del espín del electrón de valencia. Introducida su adecuada cuantización, se justificó el resultado experimental observado.
El espín es una propiedad sin análogo clásico, es decir, no hay correlato en Física Clásica; para ella, simplemente, no existe. Así que, si lo ha leído alguna vez, olvídelo: el espín no tiene nada que ver con un momento angular de rotación de una partícula, aparte de compartir unidades. Y es que si se usa el valor estimado para el radio clásico» del electrón y el momento angular total conocido del electrón, se concluye que un punto en el ecuador del electrón ¡se movería a unas 137 veces la velocidad de la luz! Así, aunque se siga en algunos contextos usando la palabra “giro”, es otro abuso de lenguaje para referir realmente al espín o momento angular intrínseco. Pervive, por ejemplo, en la denominación frecuente del factor de Landé g como factor «giromagnético».
Las siguientes figuras nos indican lo que sucede experimentalmente si hacemos pasar fermiones de espín $\frac{1}{2}$ bien por un dispositivo Stern-Gerlach, bien por varios artilugios de medida similares, pero con distintas orientaciones, de forma sucesiva:
Resultados en un dispositivo tipo Stern-Gerlach (Autor: I. Saideh).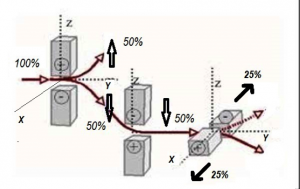

Medidas Stern-Gerlach sucesivas sobre fermiones de espín 1/2 (imagen del libro «La realidad cuántica», de RBA ediciones, colección «Un paseo por el cosmos», número 32).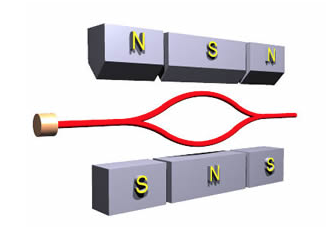

Camino de un haz de fermiones neutros de espín 1/2 en sucesivos Stern-Gerlach con polaridades de los polos magnéticos invertidas (imagen de libretexts.org).

A rellenar: las salidas en este experimento de sucesivos dispositivos Stern-Gerlach (imagen de la URL=https://www.numerade.com/).

En términos cuánticos, pues, nos encontramos con la situación que establece el siguiente postulado cuántico, formulado por B. d’Espagnat (véase “Veiled Reality. An analysis of Present-day Quantum Mechanical Concepts”, p. 223) para resumir la concepción de estado cuántico:
«A quantum system has no dynamical properties of its own whatsoever (it is therefore meaningless to think of it as having some unknown ones). When associated with a given experimental setup it can be said to have the dynamical property this setup is appropiate for measuring. The, properly so-called, measurement event (The actual interaction with the instrument) then reveals the value this dynamical property has on the system».
-Esta concepción, denominada como concepción relacional del estado cuántico, fue desarrollada por Bohr en 1935, como respuesta al argumento Einstein-Podolsky-Rosen (EPR) publicado ese mismo año y con el que se que pretendía establecer la mecánica cuántica como una teoría incompleta. En ella el objeto/sistema bajo observación y el aparato/experimento con que se le observa forman un sistema indivisible que no admite ser separado en partes analizables individualmente.
-La concepción relacional sustituyó a la antigua concepción interaccional, vigente hasta 1935, en la que los atributos microfísicos se atribuían a los sistemas en sí mismos tras su interacción con un aparato de medida. De forma que para determinar o medir las propiedades de los objetos debemos hacer experimentos, tanto en Física Clásica como en Física Cuántica, pero en la segunda, peculiarmente, las propiedades, en último término, están definidas por los experimentos que realizamos.
-La combinación de un sistema cuántico dado, por ejemplo, una «partícula» (sea cual sea el significado cuántico de este término…), con un montaje experimental concreto, para realizar una observación particular, como la medida de su observable posición, es un sistema distinto del sistema que integrarían la misma partícula con un aparato experimental diseñado para medir otra propiedad, de la misma partícula, como el momento. Y si ambos montajes experimentales son incompatibles, por ser complementarios entre sí los observables que miden ( [q, p] ≠ 0), entonces, respondió Bohr al argumento EPR, puesto que un «elemento de realidad» (concepto ajeno a la cuántica e introducido en el argumento EPR) sólo puede estar asociado con un acto concreto de medición realizado, no está justificado («es esencialmente ambiguo») considerar que posición y momento corresponden a dos elementos de realidad existentes simultáneamente, ya que nunca se pueden realizar medidas simultáneas conjuntas de posición y momento con sendas precisiones que vayan más allá del límite establecido por el principio de indeterminación. En todo caso, la mecánica cuántica ortodoxa no considera ningún tipo de «elementos de realidad», se trata de una teoría radicalmente instrumentalista que no configura una ontología en su interpretación ortodoxa, quedando estas cuestiones en el ámbito de lo que se conoce como «interpretaciones alternativas» del formalismo.
-Representación «figurativa»: según el Principio de superposición, aplicado al espín de un electrón, en ausencia de determinación de su proyección sobre una dirección cualquiera, marcada como OZ, en la correspondiente función de onda se superponen todas las orientaciones con origen en O y sobre la superficie de dos conos enfrentados por su vértice común en O (únicas compatibles con el hecho de que, bajo medida de la componente $S_z$ , el resultado sea bien $+\frac{\hbar}{2}$ ( $\uparrow$ , «hacia arriba»), bien $-\frac{\hbar}{2}$ ( $\downarrow$ , «hacia abajo»):

Representación borrosa e ideal de las orientaciones espín electrónico en superposición
Tarea formal: representar en el formalismo matemático las componentes del espín según los tres ejes coordenados ( $\vec{S}=\frac{\hbar}{2}\vec{\sigma}$ , donde $\vec{\sigma}$ representa las matrices de Pauli), y sumar vectorialmente los momentos angulares cuantizados (coeficientes de Clebsch-Gordan para el cambio entre vectores de las correspondientes bases).
Imagen de la Wikipedia.