La nueva física

double-slit-film_dibujo20120328-selected-frames-from-a-false-colour-movie-recorded-with-an-emccd-camera-showing-build-up-quantum-interference-pattern

Insuficiencia de la antigua teoría cuántica

La Antigua Teoría de los cuantos supuso un enorme progreso hacia la comprensión del microcosmos que culminaría en 1925 con las primeras formulaciones de la nueva teoría cuántica.
Alcanzado 1925, se había logrado gracias a ella la comprensión de un gran número de fenómenos inexplicables en términos de la Física Clásica, entre otros:
1. La radiancia espectral del cuerpo negro.
2. Los espectros de líneas de los sistemas monoelectrónicos (y algunos más complicados, parcialmente).
3. La estructura fina del Hidrógeno.
4. Los efectos Stark y Zeeman normal (éste también explicado por la teoría clásica) para un átomo monoelectrónico.
5. Algunas de las reglas de selección observadas para las transiciones atómicas de sistemas sencillos.
6. El efecto fotoeléctrico.
7. La presencia de una longitud de onda mínima umbral en los espectros característicos de rayos $X$ .
8. La capacidad calorífica de los sólidos a baja temperatura.
9. El efecto Compton.
10. La difracción de partículas materiales.
Sin embargo, la teoría presentaba numerosas limitaciones y defectos, y parecía que se había llegado a su límite de capacidad explicativa. La Física no conseguía avanzar en la justificación teórica de numerosos fenómenos observados con una teoría precuántica claramente insuficiente; por ejemplo:
1. La teoría sólo se podía aplicar a algunos sistemas multiperiódicos, dejando fuera todos los complejos (átomos con más de un electrón) o los no periódicos
2. Adolecía de inconsistencia, en el sentido de mezclar sin reglas fijas conceptos clásicos y cuánticos, como evidencia la dualidad onda corpúsculo.
3. No justificaba la mayoría de las reglas de selección, intensidades de líneas y polarizaciones de éstas observadas.
4. El efecto Zeeman anómalo, que se produce al situar átomos en campos magnéticos débiles, escapaba a todo intento de explicación: requeriría la introducción del concepto de espín, un momento angular intrínseco sin análogo clásico postulado en 1925 por S. Goudmit y G.E. Uhlenbeck.
5. El experimento de Stern-Gerlach requería variables sin análogo clásico para su justificación: el espín.
A partir de 1925, finalmente se logró desarrollar una teoría que superó todas estas dificultades y problemas, teniendo lugar lo que se ha dado en denominar como «revolución cuántica». Como protagonistas pioneros de ella, Heisenberg y Schrödinger en 1925, por separado y con versiones aparentemente distintas en un principio: primeros formalismos cuánticos.

Introducción: sobre ondas y corpúsculos

Nuestra experiencia cotidiana sobre los fenómenos en la Naturaleza carece de ambigüedades sobre los conceptos teóricos clásicos de partícula y onda. Ambos términos se correlacionan con entidades observacionales que tienen en común tan sólo, aparentemente, la capacidad de transportar energía y momento entre diferentes regiones del espacio.
Así pues, en el dominio de la Física Clásica, el de nuestra realidad macroscópica, ondas y partículas conforman una ontología que los integra como elementos diferentes y separados: las correspondientes disciplinas Óptica y Mecánica refieren y explican experimentos involucrando sus términos teóricos propios representativos, a partir del enunciado de leyes y principios de aplicación en campos de fenómenos usualmente separados.
Como ilustración característica, la naturaleza de la luz fue objeto de un largo debate científico, que se extendió durante siglos: chorro de corpúsculos para Newton pero onda para Huyguens (s. XVII); onda con Young y, definitivamente, Maxwell, en el s. XIX; vuelta a la teoría corpuscular con Einstein en el s.XX; naturaleza dual con el desarrollo de la Física Cuántica… hasta la Electrodinámica Cuántica.
Porque… ¿qué es un fotón?
Y es que los fenómenos que percibimos, a lo mejor radicados en una realidad física subyacente, sobre todo cuando conciernen con lo microscópico, con átomos, núcleos, partículas elementales, etc., requieren para su explicación teórica de una nueva física, la Física Cuántica, en la que los términos teóricos de partícula y onda se desdibujan, apareciendo otros nuevos que integran características y propiedades que sus correlatos clásicos, cuando las poseían, lo hacían por separado.

La dualidad onda-corpúsculo

Por ejemplo: los electrones, que hemos visto como, tras aparecer como meras unidades elementales de carga en el contexto de los experimentos pioneros de electrólisis, pasaban a ser partículas materiales elementales integrantes de los rayos catódicos, comportándose como tales, siguiendo las leyes de la Mecánica, en dispositivos tan comunes como los tubos de las antiguas televisiones. Pero también se convirtieron en protagonistas de experimentos de difracción, tradicionalmente reservados a las ondas. Y la radiación electromagnética, la onda eje central del Electromagnetismo, interviene en fenómenos para cuya explicación resultó muy útil apelar a una concepción cuasi corpuscular (efecto fotoeléctrico, longitud de onda umbral mínima en los espectros continuos de rayos $X$ , dispersión Compton…).

Hitos fundamentales en la concepción de la dualidad onda-corpúsculo:
1. El cuanto de luz de Einstein:
  1. Einstein: en 1905, en un artículo titulado «Un punto de vista heurístico sobre la producción y transformación de la luz«, mostró como la idea de un cuanto de luz podía explicar el efecto fotoeléctrico y la presencia de una frecuencia característica para cada material por debajo de la cual no se producía ningún efecto:
    «Si la radiación monocromática de baja densidad se comporta en aspectos termodinámicos como un medio discreto que consistiera de quanta de energía mutuamente independientes de magnitud $\frac{R\beta \nu}{N}$ ( $\beta=\frac{h}{k},\, k=\frac{R}{N},\, \frac{R\beta \nu}{N}=h\nu$ , hipótesis del cuanto de luz), entonces esto sugiere como si las leyes de generación y conversión de la luz se dieran también como si la luz consistiera de cuantos de energía de esta clase». Por lograr explicar la ley del efecto fotoeléctrico con esta hipótesis heurística recibiría el Premio Nobel de Física en 1921.
  2. Einstein conceptualiza la radiación como compuesta de paquetes indivisibles de energía o «cuantos de luz» («fotones» a partir de 1926, en terminología introducida por Lewis), que se desplazan localizadamente a velocidad $c$ (vacío); para una frecuencia $\nu$ , la energía del cuanto es $E = h \nu$ ; les dotaría de momento en 1916.
2. Las ondas de materia de de Broglie:
  1. En 1924 L. de Broglie presenta su Tesis Doctoral, en la cual postula las ondas de materia.
  2. Hipótesis: la idea básica de la teoría cuántica es la imposibilidad de considerar «una porción aislada de energía» sin asignarle una frecuencia $\nu$ : apelación a la relación de Einstein $E=h \nu$ de los cuantos de luz (fotones).
  3. Tesis: Las partículas materiales, también «porciones aisladas de energía», deberían ser tratadas análogamente, asociándoles una longitud de onda $\lambda$ : relación de de Broglie $\lambda = \frac{h}{p}$ (postulación de las ondas de fase o materia).
3. La complementariedad de Bohr:
  1. En 1927 Bohr hace públicas sus nuevas concepciones al respecto, en la ponencia que presentó en el Congreso de Como, titulada «El postulado cuántico y el desarrollo reciente de la teoría cuántica» (Bohr, N.; «Das Quantenpostulat und die neuere Entwicklung der Atomistik», Die Naturwissensenschaften 16 (1928) 245-257; «The Quantum Postulate and the Recent Development of the Atomic Theory», Nature 121 (1928) 580-590; rep. en [WHE-83], pp. 87-126.
    1. La base del artículo es la aceptación de la dualidad onda-corpúsculo, a la que Bohr se había opuesto inicialmente, al negarse a reconocer la validez de los cuantos de luz introducidos por Einstein (ver entrada primeras controversias Einstein-Bohr).
    2. Contenido esencial del artículo:
      -Parte del «postulado cuántico», por el que se reconoce una «discontinuidad esencial en los procesos atómicos«; esta discontinuidad, «desconocida en el mundo clásico y representada por el cuanto de acción de Planck h,»produce consecuencias fundamentales en el contenido de realidad física asignado a los fenómenos microscópicos y a sus agentes de observación«:
      «Notwithstanding the difficulties which, hence, are involved in the formulation of the quantum theory, it seems, as we shall see, that its essence may be expressed in the so-called quantum postulate, which attributes to any atomic process an essential discontinuity, or rather individuality, completely foreign to the classical theories and symbolized by Planck’s quantum of action.(…). This postulate implies a renunciation as regards the causal space-time coordination of atomic processes. Indeed, our usual description of physical phenomena is based entirely on the idea that the phenomena concerned may be observed without disturbing them appreciably.(…). Now, the quantum postulate implies that any observation of atomic phenomena will involve an interaction with the agency of observation not to be neglected» (N. Bohr, cit. en Petersen, A.; «The Philosophy of Niels Bohr», en [FRE-85], pp. 299-310).
    3. Aceptado el postulado, se deriva la aceptación también de una interacción finita e impredecible entre el objeto sobre el que se mide y el instrumento de medida, siendo su consecuencia una indeterminación en el conocimiento de su mutua interacción.
    4. Aceptar el postulado, además, imposibilita una definición clásica del estado del sistema, pues «la noción clásica del mismo requiere la no existencia de perturbación externa, con lo que la observación misma se haría imposible, perdiendo los conceptos de espacio y tiempo su sentido«.
    5. Y también se hace imposible la causalidad:
      «De otro lado, si para hacer las observaciones posibles se admiten las interacciones del sistema con adecuados aparatos de medida externos al sistema, ya no es posible una definición no ambigua del estado del sistema, siendo imposible la causalidad en el sentido estricto del término«.
      Así pues, la propia naturaleza de la M.C. fuerza a considerar las dos descripciones, la espacio-temporal (cinemática: $\vec{r}, t$ ) y la causal (dinámica: $E, \vec{p}$ ), características de las teorías clásicas, como «complementarias«, en el sentido de mutuamente excluyentes e igualmente necesarias.
    6. Renuncia al modo clásico de descripción:
      «[The quantum postulate] forces us to adopt a new mode of description designated as complementary in the sense that any given application of classical concepts precludes the simultaneous use of other classical concepts which in a different connection are equally necessary for the elucidation of phenomena». (N. Bohr, cit. en [JAM-74], p. 95).
      -Mientras que en Física Clásica es posible concebir un experimento o aparato experimental que en una sola operación nos proporcione toda la información sobre el objeto bajo estudio, en Física Cuántica no es posible.
      -En el dominio de la experiencia que la Física Cuántica describe, podemos montar un aparato para medir la posición o el momento de la partícula, pero no uno que mida ambos simultáneamente. Consecuentemente, carece de sentido atribuir tales propiedades al sistema en sí mismo.
      -Y lo mismo es cierto para cualquier par de observables complementarios.
    7. El artículo incluye también una deducción de las relaciones de indeterminación.
    8. La formulación original de Como contenía implicaciones problemáticas que llevarían a Bohr, posteriormente, a su remodelación. Por ejemplo: implícitamente, se suponía una distinción entre, de un lado, los sistemas como existen y, de otra, como son conocidos. Pero lo único que se afirmaba sobre tales sistemas eran las condiciones de su cognoscibilidad.
      -Así, se suponía que un sistema estaba en un estado dado, determinado antes de la medida, siendo la medida la que lo perturbaba en ese estado anterior, forzando a un cambio de estado. Al mismo tiempo, ambos estados se afirmaban como incognoscibles.
  2. Concepción de estado cuántico en Bohr:
    1. Concepción interaccional de estado: Es la original, contenida en la ponencia presentada en Como, 1927, anterior a la formulación del argumento Einstein-Podolsky-Rosen, que tendría lugar en 1935.
      -Se basa en la noción de interacción física: afirmar que una partícula tiene un momento definido p implica afirmar que dicha partícula ha sido sometida a una interacción con un aparato de medida que ha registrado el valor p.
      The Bohr postulate: «A quantum system has no dynamical properties of its own whatsoever (it is therefore meaningless to think of it as having some unknown ones). When associated with a given experimental setup it can be said to have the dynamical property this setup is appropiate for measuring. The, properly so-called, measurement event (the actual interaction with the instrument) then reveals the value this dynamical property has on the system«.
      (B. d’Espagnat, en [ESP-95], p. 223).
    2. Concepción relacional de estado: Tras la publicación del teorema EPR, Bohr ha de revisar su concepción anterior, la interaccional de Como, evolucionando hacia una relacional, en la que el objeto bajo observación y el aparato de medida forman un sistema indivisible, no susceptible de separación en partes para su análisis.
      -La descripción del estado de un sistema, por tanto, no se puede restringir al sistema bajo observación, puesto que ha de expresar una relación entre el sistema y el montaje experimental involucrado en la medida.
      -El sistema cuántico y el aparato de medida u observación forman un todo indivisible.
      -Para determinar las propiedades de los objetos debemos, tanto en Física Clásica como en Física Cuántica, hacer experimentos, pero en la segunda, peculiarmente, las propiedades, en último término, están definidas por los experimentos que realizamos.
      Principle of Complementarity: «The nonseparable whole constituted by the quantum system and a definite instrument can be described by using a simplification of our language, according to which some of the properties that the system and the instrument share with one another are conventionally attributed to the system. However, other properties, which in our classical experience leads us to think of, cannot then be attributed to the system. They are said to be complementary to the first ones. They can also be attributed to a quantum system similar in type to the one considered so far, but this is possible only if that system builds up an indivisible whole with some new instrument, which is appropriate for a measurement of the new quantities«. (Cf. B. d’Espagnat, en [ESP-76], p. 252).
  3. Bohr mantuvo sus ideas en revisión continua desde su primera formulación en Como, 1927. Se considera (ver referencias al pie de la entrada) que hacia 1937 su postura epistemológica quedó fijada, culminando una transición desde la complementariedad original expuesta en Como, esencialmente cinemático-dinámica, centrada en la imposibilidad simultánea de ambas descripciones, espacio-temporal y causal, para los sistemas cuánticos, hacia la nueva concepción antes sumarizada.
  4. Y, respecto a la dualidad onda-corpúsculo, debe separarse del anterior principio de complementariedad: no existen observables «onda» y «corpúsculo», a los que asociar sendos operadores autoadjuntos que no conmuten entre sí: conviene ser consciente de que «la Física se mueve«, y hoy la complementariedad original de Bohr debe ser reelaborada para dar cuenta de recientes fenómenos, especialmente en el campo de la Óptica Cuántica. Una buena puesta al día puede iniciarse leyendo el siguiente artículo, y las referencias en él, en su caso:
    García Alcaine, G.; «Complementaridad, coherencia, dualidad», Revista Española de Física 6,3 (1993) 8-9.
    -De manera que las propiedades ondulatorias y corpusculares pueden manifestarse simultáneamente, en un único experimento. La versión original de Bohr de la complementariedad onda-corpúsculo queda restringida al caso en que uno de los dos tipos de conducta, o propiedades, se haya manifestado de forma «total», pero existen situaciones intermedias en que ambos tipos de propiedades se ponen de manifiesto a la vez: recuérdese el experimento del doble prisma de Bose.
  5. Lectura clarificadora: «Another Step Back for Wave-Particle Duality», en http://physics.aps.org/articles/v4/102 :
    «We show you can do both wave and particle experiments at once» (…). This means the choice of wave vs particle can be delayed indefinitely. The photon can be observed at one of the detectors and still not ‘know’ if it is supposed to be a wave or a particle. It’s only when the observer decides to measure the state of the quantum control that the photon’s behavior can be identified as wave-like or particle-like.

¿Onda o corpúsculo? Ψ

El formalismo cuántico es suficiente para predecir correctamente todos los resultados observados hasta la fecha (óptica cuántica, QED, operadores de campo eléctrico y magnético, etc.).
Sólo el requerir una comprensión que incorpore imágenes o representaciones mentales subyugadas a las percepciones cotidianas hace aparecer términos conceptuales ontológicos (onda, partícula), sin relevancia de orden predictivo. De hecho, en la moderna Teoría Cuántica de Campos se prescinde por completo de esos términos en su significado clásico: las partículas se convierten en excitaciones de los campos cuánticos, y estos en los componentes ontológicos de la realidad (en opinión de muchos).
Por ejemplo, en un experimento de doble rendija, es hora de cambiar narrativas del tipo «cada partícula pasa por las dos rendijas e interfiere consigo mismo», sustituyéndolas por, en este ejemplo, expresiones como «cuando los dos caminos son indistinguibles, las probabilidades asociadas a cada uno (las $\psi$ ) interfieren entre sí».
En palabras de Bohr:
Is absolutely meaningless to ask whether light is ‘in reality’ waves or particles. We must never forget that ‘reality’ too is a human word just like ‘wave’ or ‘consciousness’. Our task is to learn to use these words correctly, that is, unambiguosly and consistently. (Bohr, 1967, cit. por Kalckar en [WHE-85], p.5).
Ya lo advirtió Heisenberg:
The concept of complementarity introduced by Bohr into the interpretation of quantum theory has encouraged the physicists to use an ambiguous rather than an unambiguous language, to use the classical concepts in a somehow vague manner.
(Heisenberg, 1958, cit. en Ghose and Home, Wave-Particle Duality of Single-Photon States, Foundations of Physics, 22-12, 1992, p. 1446).
Y concluía:
When this vague and unsystematic use of the language leads into difficulties, the physicist has to withdraw into the mathematical scheme and its unambiguous correlation with the experimental facts. (Heisenberg, 1958, ibid.)

Formulario ondas de materia

$\nu=\frac{E}{h}$ ; $\lambda=\frac{h}{p}$

Dominio relativista	Aproximación no relativista	Comentarios
$E_r^2=m_0^2c^4+p_r^2c^2=m^2c^4$	$E_{nr}=\frac{p_{nr}^2}{2m_0}=K_{nr}$	(es usual ignorar la energía en reposo $m_0c^2$ en $E_{nr}$ )
$p_r=mv=\frac{m_0v}{\sqrt{1-\frac{v^2}{c^2}}}$	$p_{nr}=m_0v$
$K_r=E_r-m_0c^2$	$K_{nr}=E_{nr}=\frac{p_{nr}^2}{2m_0}=\frac{1}{2}m_0v^2$

$\lambda_r=\frac{h}{p_r}=\frac{h}{mv}=\frac{h\sqrt{1-\frac{v^2}{c^2}}}{m_0v}$	$\lambda_{nr}=\frac{h}{p_{nr}}=\frac{h}{m_0v}$
$\nu=\frac{mc^2}{h}=\frac{m_0c^2}{h\sqrt{1-\frac{v^2}{c^2}}}$
$\nu=\frac{+\sqrt{m_0^2c^4+p_r^2c^2}}{h}=\frac{mc^2}{h}$	Nota: $lim_{v < < c}\nu=\frac{m_0c^2}{h}=\nu_0$	( $\nu$ sin significado físico en Mec. Cuánt.)
$h^2\nu^2\lambda^2=m_0^2c^4\lambda^2 + h^2c^2$	$\nu=\frac{h}{2m_0\lambda^2}$
En general:
$E=h\nu =\hbar \omega$ $p=\hbar k$		( $k=\frac{2\pi}{\lambda}$ es el número de ondas)
En general, para una onda de de Broglie:
$v_B=\nu \lambda=\frac{\omega}{k}=\frac{mc^2}{h}\lambda=\frac{c^2}{v}$ $k=\frac{2\pi mv}{h}=\frac{2\pi m_0v}{h\sqrt{1-\frac{v^2}{c^2}}}$ $\omega=2\pi \nu=\frac{2\pi}{T}=\frac{\hbar k^2}{2m}$		(la veloc. de fase puede ser $v_B > c$ )
$v_g=\frac{d \omega}{d k}=v$		(la veloc. de grupo $v_g$ coincide con la veloc. $v$ de la part. )

Formulario radiación-materia

Onda (límite clásico: $h \rightarrow 0$ )	Corpúsculo (límite clásico: $\lambda_B \rightarrow 0$ )	Comentarios
$E=h\nu$	$\nu=\frac{E}{h}$
$p=\frac{h\nu}{c}$	$\lambda=\frac{h}{p}$
$E=h\nu=\hbar \omega$	$E=h\nu=\hbar \omega$
$p=\frac{h}{\lambda}= \hbar k$	$p=\frac{h}{\lambda}= \hbar k$
$E=pc$	$E^2=m_0^2c^4+p^2c^2=m^2c^4$ $E=K+m_0c^2$	-relativista.
$\omega=kc$	$\omega=\frac{\hbar k^2}{2m}$
$\frac{d^2 \omega}{dk^2}=0$	$\frac{d^2 \omega}{dk^2}=\frac{\hbar}{m}$	-para la radiación no hay dispersión; para la materia sí.
$\nu \lambda=\frac{E}{p}=c$	$\nu \lambda=\frac{E}{p}=\frac{c^2}{v}=v_B$	-la vel. de fase puede ser $v_B \ge c$ .
$\nu \lambda=\frac{E}{p}=c$	$v_g=\frac{d \omega}{d k}=v$	(la veloc. de grupo $v_g$ coincide con la veloc. $v$ de la part. )
$\nu=\frac{c}{\lambda}$	$\nu=\frac{c^2}{v \lambda}$

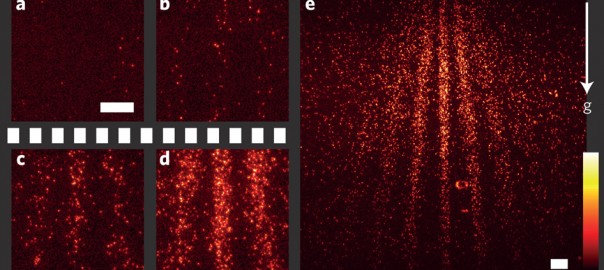
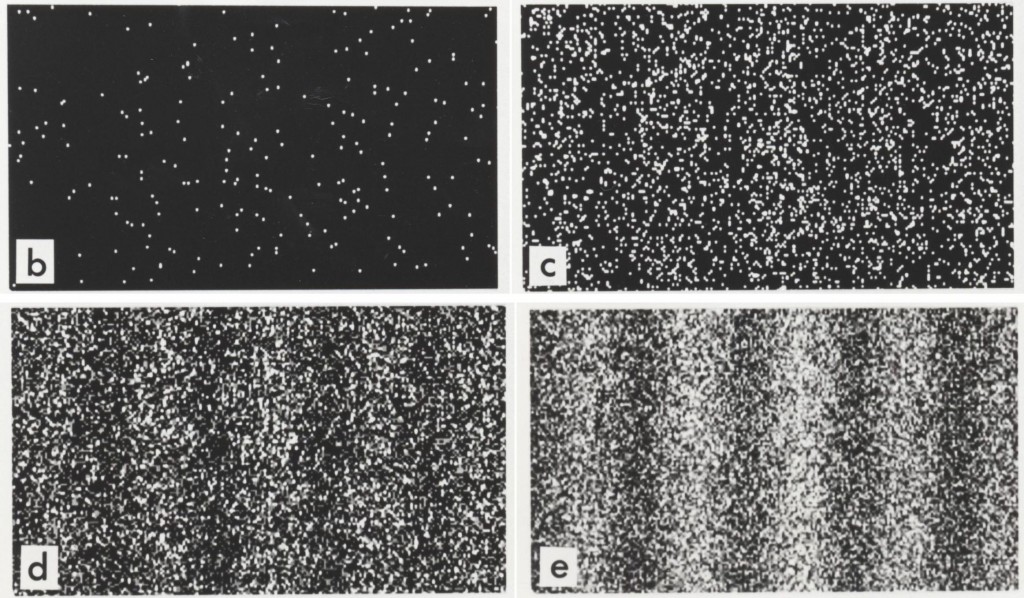
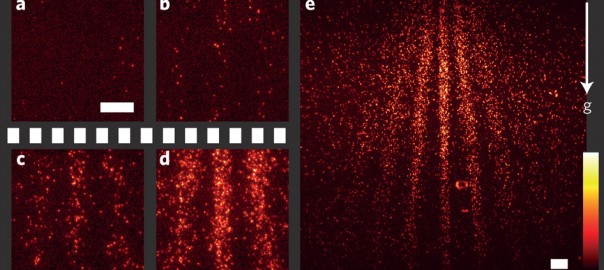
El experimento de la doble rendija

*Secuencia de resultados del experimento de Tonomura en Hitachi, 1989, con electrones lanzados uno a uno (imagen licencia Creative Commons de Wiki).*

http://www.hitachi.com/rd/portal/research/em/doubleslit.html

http://rdg.ext.hitachi.co.jp/rd/moviee/doubleslite-n.wmv

http://www.youtube.com/watch?v=_oWRI-LwyC4

http://la-mecanica-cuantica.blogspot.com.es/2009/08/ondas-de-materia.html

http://www.investigacionyciencia.es/blogs/fisica-y-quimica/31/posts/y-el-experimento-de-la-doble-rendija-se-hizo-realidad-11103

http://francis.naukas.com/2012/03/28/video-en-tiempo-real-del-experimento-cuantico-de-doble-rendija-con-moleculas-de-ftalocianina/

*Vídeo en: https://www.youtube.com/watch?v=NUS6_S1KzC8*

-Vídeo:
((subido por Francis Villatoro).

*Animación procedente de: https://www.ph.utexas.edu/~coker2/index.files/diff.htm.*

Referencias

[BEI-87] Beiser, A.; Concepts of Modern Physics, McGraw-Hill, Singapore, 1987.

[ESP-76] Espagnat, B.D’; Conceptual Foundations of Quantum Mechanics, Benjamin, 1976.

[FRE-85] French, A.P. and Kennedy, P.J.; Niels Bohr: a centenary volume, Harvard Univ. Press, 1985.

[JAM-74] Jammer, M.; The philosophy of Quantum Mechanics, Wiley, 1974.

[MEH-82] Mehra,J., Rechenberg,H.; The Historical Development of Quantum Mechanics, 6 vol., Springer-Verlag, Nueva York, 1982.

[WHE-83] Wheeler, J.A. y Zurek,W.H., ed.; Quantum Theory and measurement, Princenton Univ., Princenton, 1983.

Páginas complementarias

García Alcaine, G.; «Complementaridad, coherencia, dualidad», Revista Española de Física 6,3 (1993) 8-9.

Tonomura, A., Endo, J., Matsuda, T., Kawasaki, T. and Ezawa, H.; «Demonstration of single-electron buildup of an interference pattern», American Journal of Physics 57, 1989, pp. 117-120.

Cálculos en el experimento de Young

http://cnx.org/contents/031da8d3-b525-429c-80cf-6c8ed997733a:216/College_Physics

http://francis.naukas.com/2013/12/02/francis-en-trendingciencia-la-realidad-esta-hecha-de-campos-de-particulas/

http://www.physics.ohio-state.edu/~aubrecht/Faculty.pdf

APPS:

http://demonstrations.wolfram.com/WaveParticleDualityInTheDoubleSlitExperiment/

Wave-Particle Duality in the Double-Slit Experiment from the Wolfram Demonstrations Project by S. M. Blinder