Teletransporte cuántico
![]() La palabra “teletransporte”, atendiendo a su etimología, referiría al fenómeno por el que algo se traslada a distancia. Dicho así, no suena muy revolucionario, pero si se añade la característica de realizar ese transporte entre dos regiones del espacio, sin recorrer las zonas intermedias y de forma instantánea, empieza ya a sonar a ciencia-ficción… y a violación de la Relatividad. El caso es que, aprovechando el entrelazamiento cuántico, hoy en día se han hecho ya reales los experimentos de «teleportación» (palabra que no existe en español, pero que se está imponiendo para hacer hincapié en que el fenómeno cuántico no consiste en el transporte instantáneo de energía o materia de un lado a otro), por supuesto respetando a rajatabla los postulados de la teoría de la Relatividad. Expliquemos en qué consisten.
La palabra “teletransporte”, atendiendo a su etimología, referiría al fenómeno por el que algo se traslada a distancia. Dicho así, no suena muy revolucionario, pero si se añade la característica de realizar ese transporte entre dos regiones del espacio, sin recorrer las zonas intermedias y de forma instantánea, empieza ya a sonar a ciencia-ficción… y a violación de la Relatividad. El caso es que, aprovechando el entrelazamiento cuántico, hoy en día se han hecho ya reales los experimentos de «teleportación» (palabra que no existe en español, pero que se está imponiendo para hacer hincapié en que el fenómeno cuántico no consiste en el transporte instantáneo de energía o materia de un lado a otro), por supuesto respetando a rajatabla los postulados de la teoría de la Relatividad. Expliquemos en qué consisten.
![]() Bowmeester et al, Experimental quantum teleportation, Nature 390 (1997) 575 (también disponible en arXiv.org: 1901.11004v1.pdf):
Bowmeester et al, Experimental quantum teleportation, Nature 390 (1997) 575 (también disponible en arXiv.org: 1901.11004v1.pdf):
![]() El sueño de la teleportación es ser capaz de viajar mediante la simple reaparición en un lugar distante […]. Para hacer una copia de ese objeto en un lugar distante no se necesitan las partes y piezas originales; todo lo que se necesita es enviar la información escaneada, de modo que pueda usarse para reconstruir el objeto.
El sueño de la teleportación es ser capaz de viajar mediante la simple reaparición en un lugar distante […]. Para hacer una copia de ese objeto en un lugar distante no se necesitan las partes y piezas originales; todo lo que se necesita es enviar la información escaneada, de modo que pueda usarse para reconstruir el objeto.
![]() ¡Pero ni Star Trek (no hay transporte de materia ni energía) ni fax cuántico (no se consigue disponer a la vez de un original y una copia de él)!
¡Pero ni Star Trek (no hay transporte de materia ni energía) ni fax cuántico (no se consigue disponer a la vez de un original y una copia de él)!
![]() Problema: ¿Cómo obtener la información precisa requerida sobre el original?
Problema: ¿Cómo obtener la información precisa requerida sobre el original?
-Porque, a diferencia de lo que ocurre en el mundo clásico, en el cuántico las moléculas, átomos, electrones… están sujetos a la indeterminación cuántica.
![]() Teorema de no-clonación de estados cuánticos:
Teorema de no-clonación de estados cuánticos:
![]() 1982, W. K. Wooters and W. H. Zurek, A single quantum cannot be cloned, Nature 299 (1982) 802 – 803.
1982, W. K. Wooters and W. H. Zurek, A single quantum cannot be cloned, Nature 299 (1982) 802 – 803.
![]() Abstract: If a photon of definite polarization encounters an excited atom, there is typically some nonvanishing probability that the atom will emit a second photon by stimulated emission. Such a photon is guaranteed to have the same polarization as the original photon. But is it possible by this or any other process to amplify a quantum state, that is, to produce several copies of a quantum system (the polarized photon in the present case) each having the same state as the original? If it were, the amplifying process could be used to ascertain the exact state of a quantum system: in the case of a photon, one could determine its polarization by first producing a beam of identically polarized copies and then measuring the Stokes parameters. We show here that the linearity of quantum mechanics forbids such replication and that this conclusion holds for all quantum systems.
Abstract: If a photon of definite polarization encounters an excited atom, there is typically some nonvanishing probability that the atom will emit a second photon by stimulated emission. Such a photon is guaranteed to have the same polarization as the original photon. But is it possible by this or any other process to amplify a quantum state, that is, to produce several copies of a quantum system (the polarized photon in the present case) each having the same state as the original? If it were, the amplifying process could be used to ascertain the exact state of a quantum system: in the case of a photon, one could determine its polarization by first producing a beam of identically polarized copies and then measuring the Stokes parameters. We show here that the linearity of quantum mechanics forbids such replication and that this conclusion holds for all quantum systems.
![]() W. K. Wootters & W. H. Zurek: The No-Cloning theorem.
W. K. Wootters & W. H. Zurek: The No-Cloning theorem.
![]() The No-Cloning theorem (n-Lab):
The No-Cloning theorem (n-Lab):

![]() D. Dieks, Communication in EPR devices, Physics Letters A 92 (1982) 271-272; en sciencedirect.com.
D. Dieks, Communication in EPR devices, Physics Letters A 92 (1982) 271-272; en sciencedirect.com.
Es imposible, en general, realizar una copia perfecta o clon de un sistema individual cuántico arbitrario.
-Ya que, para copiarlo, habría que mirarlo, y entonces (postulado de proyección o colapso) se alteraría indefectiblemente: obtener la información cuántica requerida conlleva alterar las distribuciones de probabilidad para todos los observables complementarios a los medidos. Mención aparte de que la contextualidad de muchos observables cuánticos invalida la mera idea de la «clonación» de un estado cuántico, aunque no, como veremos, la de su «replicación«.
-Y es que, apelando ahora a las relaciones de indeterminación: si, para copiar un estado cuántico, lo «miramos», entonces alteramos o destruimos inevitablemente el original: la duplicación del estado cuántico de un sistema individual arbitrario es imposible. Es decir: es imposible averiguar cuál es el estado cuántico de un sistema individual arbitrario y clonarlo, preparando copia(s) de él. Por supuesto, si sabemos cómo ha sido preparado, entonces sí que podremos disponer de un conjunto estadístico o ensemble cuántico de sistemas idénticos e igualmente preparados a él, y en este caso sí que podemos determinar su , a partir del conjunto de medidas requeridas en cada caso.
-Sólo hay una excepción: se pueden clonar estados individuales ortogonales. Por ejemplo, el análogo de un bit clásico: bien , bien
; o, también, un conjunto de estados mutuamente ortogonales, como un par
. Pero no se puede clonar una superposición general
, por la linealidad y la unitariedad requeridas, véase:
![]() A. Galindo, «El extraño y prodigioso mundo de los quanta».
A. Galindo, «El extraño y prodigioso mundo de los quanta».
![]() La linealidad de la Mecánica Cuántica exige que no puedan existir dispositivos que puedan clonar estados cuánticos desconocidos y arbitrarios. La unitariedad de la evolución en Mecánica Cuántica implica que no es posible clonar estados cuánticos distintos y no ortogonales.
La linealidad de la Mecánica Cuántica exige que no puedan existir dispositivos que puedan clonar estados cuánticos desconocidos y arbitrarios. La unitariedad de la evolución en Mecánica Cuántica implica que no es posible clonar estados cuánticos distintos y no ortogonales.
-Es imposible en general, pues, preparar un conjunto estadístico o ensemble cuántico de fotones cuánticamente idénticos a uno original dado, porque ello daría acceso a su , violando así el teorema de no-clonación, consecuencia matemática del formalismo cuántico.
![]() Pero sí va a ser posible, vía el entrelazamiento, replicar un estado cuántico de un sistema individual arbitrario a distancia. Lo que no significa clonación: el original queda destruido. Es a este fenómeno a lo que se denomina «teleportación cuántica«.
Pero sí va a ser posible, vía el entrelazamiento, replicar un estado cuántico de un sistema individual arbitrario a distancia. Lo que no significa clonación: el original queda destruido. Es a este fenómeno a lo que se denomina «teleportación cuántica«.
![]() En 1993, Bennet sugirió usar el entrelazamiento cuántico para lograr este teletransporte de estado cuántico:
En 1993, Bennet sugirió usar el entrelazamiento cuántico para lograr este teletransporte de estado cuántico:
![]() C. H. Bennett, G. Brassard, C. Crépeau, R. Jozsa, A. Peres, and W. K. Wootters, Teleporting an unknown quantum state via dual classic and Einstein-Podolsky-Rosen channels, Phys. Rev. Lett. 70 (1993) 1895-1899.
C. H. Bennett, G. Brassard, C. Crépeau, R. Jozsa, A. Peres, and W. K. Wootters, Teleporting an unknown quantum state via dual classic and Einstein-Podolsky-Rosen channels, Phys. Rev. Lett. 70 (1993) 1895-1899.
Experimentos: Teletransportando con fotones
![]() Las dos realizaciones experimentales pioneras del fenómeno del teletransporte cuántico fueron:
Las dos realizaciones experimentales pioneras del fenómeno del teletransporte cuántico fueron:
![]() 1997: Innsbruck (equipo de Zeilinger et al); 1998: Roma (equipo de Martini et al):
1997: Innsbruck (equipo de Zeilinger et al); 1998: Roma (equipo de Martini et al):
![]() Bowmeester, Pan, Matle, Eibl, Weinfurter and Zeilinger, Experimental quantum teleportation, Nature 390 (1997) 575:
Bowmeester, Pan, Matle, Eibl, Weinfurter and Zeilinger, Experimental quantum teleportation, Nature 390 (1997) 575:
![]() The dream of teleportation is to be able to travel by simply reappearing at some distant location. An object to be teleported can be fully characterized by its properties, which in classical physics can be determined by measurement. To make a copy of that object at a distant location one does not need the original parts and pieces -all that is needed is to send the scanned information so that it can be used for reconstructing the object. But how precisely can this be a true copy of the original? What if these parts and pieces are electrons, atoms and molecules? What happens to their individual quantum properties, which according to the Heisenberg’s uncertainty principle cannot be measured with arbitrary precision?
The dream of teleportation is to be able to travel by simply reappearing at some distant location. An object to be teleported can be fully characterized by its properties, which in classical physics can be determined by measurement. To make a copy of that object at a distant location one does not need the original parts and pieces -all that is needed is to send the scanned information so that it can be used for reconstructing the object. But how precisely can this be a true copy of the original? What if these parts and pieces are electrons, atoms and molecules? What happens to their individual quantum properties, which according to the Heisenberg’s uncertainty principle cannot be measured with arbitrary precision?
![]() Abstract: Quantum teleportation -the transmission and reconstruction over arbitrary distances of the state of a quantum system- is demonstrated experimentally. During teleportation, an initial photon which carries the polarization that is to be transferred and one of a pair of entangled photons are subjected to a measurement such that the second photon of the entangled pair acquires the polarization of the initial photon. This latter photon can be arbitrarily far away from the initial one. Quantum teleportation will be a critical ingredient for quantum computation networks.
Abstract: Quantum teleportation -the transmission and reconstruction over arbitrary distances of the state of a quantum system- is demonstrated experimentally. During teleportation, an initial photon which carries the polarization that is to be transferred and one of a pair of entangled photons are subjected to a measurement such that the second photon of the entangled pair acquires the polarization of the initial photon. This latter photon can be arbitrarily far away from the initial one. Quantum teleportation will be a critical ingredient for quantum computation networks.
![]() Boschi, D., Branca,S., De Martini, F., Hardy, L. and Popescu, S., Experimental realization of teleporting an unknown pure quantum state via dual classical and Einstein-Podolsky-Rosen channels, Phys. Rev. Lett. 80 (1998) 1121-1125; también en arxiv.org y en semanticscholar.org:
Boschi, D., Branca,S., De Martini, F., Hardy, L. and Popescu, S., Experimental realization of teleporting an unknown pure quantum state via dual classical and Einstein-Podolsky-Rosen channels, Phys. Rev. Lett. 80 (1998) 1121-1125; también en arxiv.org y en semanticscholar.org:
![]() Abstract: We report on a quantum optical experimental implementation of teleportation of unknown pure quantum states. This realizes all the nonlocal aspects of the original scheme proposed by Bennett et al. and is equivalent to it up to a local operation. We exhibit results for the teleportation of a linearly polarised state and of an elliptically polarised state. We show that the experimental results cannot be explained in terms of a classical channel alone.
Abstract: We report on a quantum optical experimental implementation of teleportation of unknown pure quantum states. This realizes all the nonlocal aspects of the original scheme proposed by Bennett et al. and is equivalent to it up to a local operation. We exhibit results for the teleportation of a linearly polarised state and of an elliptically polarised state. We show that the experimental results cannot be explained in terms of a classical channel alone.
![]() ¡Teletransporte HECHO! (pero se destruye el original: no hay duplicación).
¡Teletransporte HECHO! (pero se destruye el original: no hay duplicación).
1. Introducción teórica:
1.1 El qubit
![]() En la base de polarización Horizontal (
En la base de polarización Horizontal () / Vertical (
) el estado genérico superposición de un fotón es (en ausencia de medida, no realiza ninguna de sus dos posibilidades):
-Normalización:
![]() En términos de información: un «qubit«: en representación de la esfera de Bloch:
En términos de información: un «qubit«: en representación de la esfera de Bloch:

1.2 El entrelazamiento
![]() El teletransporte emplea estados entrelazados.
El teletransporte emplea estados entrelazados.
![]() Recordemos: en un estado entrelazado, por ejemplo, en el estado de Bell
Recordemos: en un estado entrelazado, por ejemplo, en el estado de Bell
(en términos de información, un «ebit«) ,
hay propiedades que presentan una correlación perfecta en su medida: Al medir las polarizaciones de cada uno de los fotones en un par de ellos enredados, según una dirección cualquiera, los respectivos resultados están siempre correlacionados: por ejemplo (depende del estado concreto) si uno sale H , el otro sale V , «anticorrelación» (o H, «correlación», en otros estados), y viceversa.
-Es decir, la manera correcta de enunciar la situación sería:
![]() «Siempre se obtiene (anti)correlación perfecta sobre un par entrelazado: al realizar sendas medidas de la correspondiente propiedad sobre cada partícula, los resultados (medidos el uno respecto al otro bien antes, bien después, o al mismo tiempo, según el sistema de referencia concreto elegido) se producen siempre correlacionados«:
«Siempre se obtiene (anti)correlación perfecta sobre un par entrelazado: al realizar sendas medidas de la correspondiente propiedad sobre cada partícula, los resultados (medidos el uno respecto al otro bien antes, bien después, o al mismo tiempo, según el sistema de referencia concreto elegido) se producen siempre correlacionados«:
Medida conjunta no local estocástica
-Y estas correlaciones cuánticas, en determinadas situaciones, son imposibles de justificar por cualquier teoría que asuma el realismo local como premisa.
-Obsérvese que, en esta superposición o combinación lineal, ninguna de las dos partículas se asocia con un valor definido («sharp» value) del observable polarización.
-La expresión anterior corresponde a un estado entrelazado para dos fotones, que son bosones de espín s=1, para los cuales sólo son posibles los valores m=+1, polarización circular levógira, y m=-1, polarización circular dextrógira, para el número cuántico de tercera componente (m=0 está prohibido por requisitos relativistas; puede obtenerse luz polarizada linealmente mezclando a partes iguales luz polarizada circularmente a derechas e izquierdas).
![]() Según vimos antes (ver entrada sobre entrelazamiento), para cada estado de Bell, por ejemplo, el
Según vimos antes (ver entrada sobre entrelazamiento), para cada estado de Bell, por ejemplo, el , cada qubit individual se encuentra en un estado mezcla: no se dispone de información maximal sobre él.
1.3 Los 4 estados de Bell y su producción por SPDC
![]() Expresiones de los 4 estados de Bell o pares EPR para dos qubits:
Expresiones de los 4 estados de Bell o pares EPR para dos qubits:
![]() Obtención de fotones entrelazados en polarización, en la base de Bell: proceso SPDC = Conversión paramétrica a la baja:
Obtención de fotones entrelazados en polarización, en la base de Bell: proceso SPDC = Conversión paramétrica a la baja:
-Cuando un haz láser (haz de bombeo) atraviesa determinados cristales no-lineales (como el borato de Bario beta), en cristal, de cuando en cuando, al azar, a partir de un fotón incidente se generan dos de menor energía, correlacionados en energía y momento, y con polarizaciones establecidas dependiendo del tipo de cristal, debido al requerimiento de cumplir las denominadas condiciones de ajuste de fase:
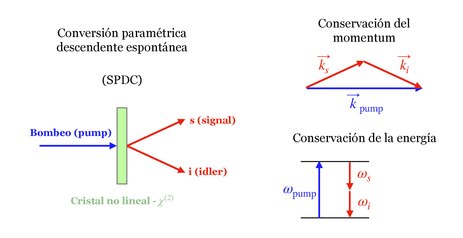
-Es pues un proceso, denominado de conversión descendente, paramétrica y espontánea (SPDC: Spontaneous parametric down-conversion), en el que en un cristal se convierte al azar un fotón incidente en un par de fotones correlacionados; el estado del cristal no se altera en el proceso, de forma que no interviene en las ecuaciones de conservación de energía y momento.
-Se trata de un proceso espontáneo que se ha convertido en un mecanismo experimental muy usado para la producción de estados monofotónicos (estados de Fock) y pares de fotones entrelazados, también en polarización con la adecuada disposición experimental.
![]() En un proceso de SPDC con type II de ajuste de fases (phase-matching II) los dos fotones correlacionados emergen sobre las superficies de sendos conos coaxiales, y con polarizaciones opuestas, de forma que el par de fotones correspondientes a los puntos de intersección de las dos superficies salen entrelazados en polarización, ya que pueden presentar cualquiera de las dos polarizaciones (horizontal H o vertical V) con igual probabilidad.
En un proceso de SPDC con type II de ajuste de fases (phase-matching II) los dos fotones correlacionados emergen sobre las superficies de sendos conos coaxiales, y con polarizaciones opuestas, de forma que el par de fotones correspondientes a los puntos de intersección de las dos superficies salen entrelazados en polarización, ya que pueden presentar cualquiera de las dos polarizaciones (horizontal H o vertical V) con igual probabilidad.
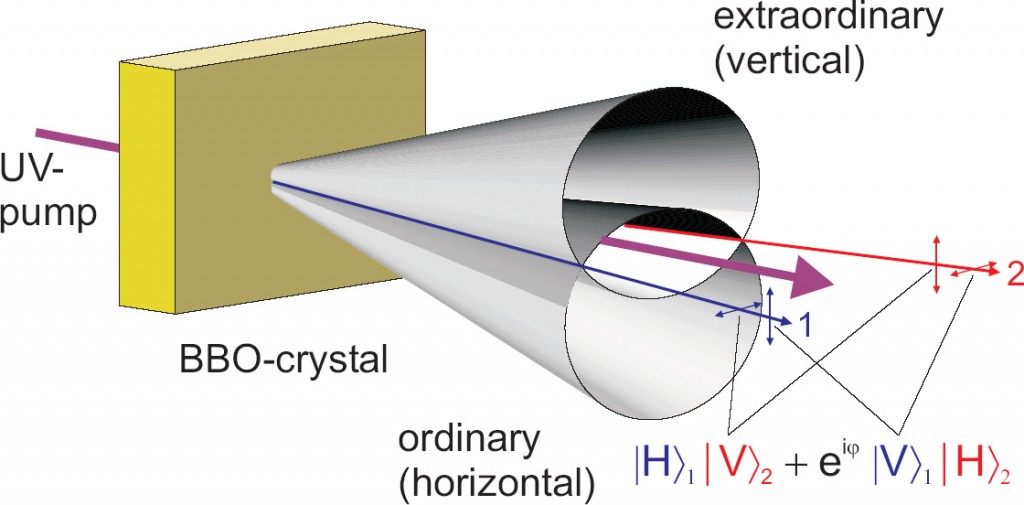
-Es decir, el estado correspondiente a este par entrelazado tiene la expresión:
donde es una fase óptica que puede después ajustarse a conveniencia usando los dispositivos adecuados (desplazadores de fase). Fijándola a los valores
y
se consigue que el par entrelazado producido se corresponda con dos sendos estados de la denominada base de Bell.
![]() También, a partir en un proceso SPDC de tipo-I , se pueden generar los otros dos estados de la base de Bell:
También, a partir en un proceso SPDC de tipo-I , se pueden generar los otros dos estados de la base de Bell:
.
![]() Fijando en las anteriores expresiones los valores de
Fijando en las anteriores expresiones los valores de como
o
, se consigue que el par entrelazado producido en cada caso se corresponda con uno de los estados de la denominada base de Bell, integrada por los cuatro vectores base conocidos como los 4 estados de Bell, mutuamente ortogonales:
![]() Los 4 estados de Bell para dos qubits:
Los 4 estados de Bell para dos qubits:
El experimento de Innsbruck: desarrollo teórico
![]() Fuente: La exposición siguiente sigue básicamente la referencia de A. Zeilinger en Investigación y Ciencia:
Fuente: La exposición siguiente sigue básicamente la referencia de A. Zeilinger en Investigación y Ciencia:
![]() A. Zeilinger, Teletransporte cuántico, Investigación y Ciencia, Temas 31, pp. 46-54; versión española del inglés «Quantum teleportation», en Scientific American, abril 2000:
A. Zeilinger, Teletransporte cuántico, Investigación y Ciencia, Temas 31, pp. 46-54; versión española del inglés «Quantum teleportation», en Scientific American, abril 2000:
![]() El propósito es teletransportar un fotón X (en rigor: el estado de un fotón):
El propósito es teletransportar un fotón X (en rigor: el estado de un fotón):
(en términos de información, un qubit).
-Alicia, en el lugar L1, desea que Benito, en L2, tenga un fotón con igual estado de polarización que el X que ella tiene y el cual desconoce, porque si lo mide alterará este estado sin lograr conocerlo.
-«Conocer el estado del fotón» significa conocer los valores de y de
, que son números complejos (se requieren pues los dos módulos y la fase relativa).
-Si el fotón X hubiese sido preparado en uno de los dos estados ortogonales de la base, entonces no habría que teletransportarlo para que Benito dispusiera de otro idéntico: bastaría informar de ello a Benito, por un canal clásico, y sin más él podría preparar otro igual: un fotón H () o V (
): casos
y
, o
y
, respectivamente.
![]() Se inicia el experimento disponiendo de dos fotones A y B entrelazados, producidos por ejemplo mediante SPDC:
Se inicia el experimento disponiendo de dos fotones A y B entrelazados, producidos por ejemplo mediante SPDC:
-Un colaborador, en L3, dispone de un par de fotones A y B entrelazados en el estado de Bell ,
,
que preserva (¡los aísla de interacciones, manteniéndolos aislados del entorno!), enviándole uno de ellos a Alicia (fotón A) y el otro a Benito (fotón B).
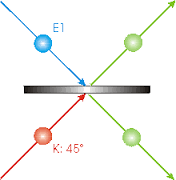
![]() A mide (en L1) sobre los fotones A y X, entrelazándolos en un estado de Bell: para ello usa un divisor de haz, o espejo semirreflector, sobre el cual cada fotón que incide tiene un 50% de probabilidad de reflejarse (y otro 50% de transmitirse). Convenientemente lanzados, dos fotones indistinguibles que llegan simultáneamente al espejo tienen un 25% de probabilidad de producir posteriormente detección en dos detectores (ver figura adjunta); en el 75% de las veces restantes sólo un detector da señal.
A mide (en L1) sobre los fotones A y X, entrelazándolos en un estado de Bell: para ello usa un divisor de haz, o espejo semirreflector, sobre el cual cada fotón que incide tiene un 50% de probabilidad de reflejarse (y otro 50% de transmitirse). Convenientemente lanzados, dos fotones indistinguibles que llegan simultáneamente al espejo tienen un 25% de probabilidad de producir posteriormente detección en dos detectores (ver figura adjunta); en el 75% de las veces restantes sólo un detector da señal.
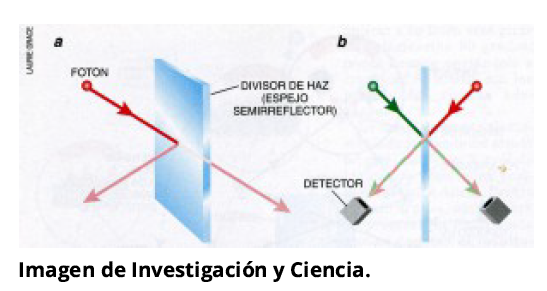
![]() Se trata de una medición conjunta, a dos qubits, o medida de detección en coincidencia (medición de estados de Bell), de la que no se obtiene información sobre las polarizaciones individuales (no estaban enredados antes de la medición, sí después: X ha cambiado):
Se trata de una medición conjunta, a dos qubits, o medida de detección en coincidencia (medición de estados de Bell), de la que no se obtiene información sobre las polarizaciones individuales (no estaban enredados antes de la medición, sí después: X ha cambiado):
![]() G. Weihs and A. Zeilinger, Photon statistics at beam splitters: an essential tool in quantum information and teleportation; artículo también disponible en semantic scholar.
G. Weihs and A. Zeilinger, Photon statistics at beam splitters: an essential tool in quantum information and teleportation; artículo también disponible en semantic scholar.
![]() Nota: sobre divisores de haz, además de la correspondiente entrada de estos apuntes, puede consultarse, por ejemplo:
Nota: sobre divisores de haz, además de la correspondiente entrada de estos apuntes, puede consultarse, por ejemplo:
![]() C. H. Holbrow, E. Galvez and M. E. Parks, Photon quantum mechanics and beam splitters, Am. J. Phys. 70, 3 (2002) 260.
C. H. Holbrow, E. Galvez and M. E. Parks, Photon quantum mechanics and beam splitters, Am. J. Phys. 70, 3 (2002) 260.

![]() Splitting a Light Beam in Two: http://physics.aps.org/story/v18/st14
Splitting a Light Beam in Two: http://physics.aps.org/story/v18/st14
![]() Interferencia bifotónica: A. Ibarra – Durán, Interferencia bifotónica en un divisor de haces, Tecnociencia 8,1 (2006) 167-181.
Interferencia bifotónica: A. Ibarra – Durán, Interferencia bifotónica en un divisor de haces, Tecnociencia 8,1 (2006) 167-181.
![]() Teletransportando:
Teletransportando:
![]() A. Zeilinger, Teletransporte cuántico, Investigación y Ciencia, Temas 31, pág. 52:
A. Zeilinger, Teletransporte cuántico, Investigación y Ciencia, Temas 31, pág. 52:
![]() Un divisor de haces, o espejo semirreflector, refleja la mitad de la luz que incide en él y transmite la otra mitad. Cada fotón tiene una probabilidad de mitad y mitad de reflejarse o de transmitirse. Si dos fotones idénticos inciden en el divisor de haz al mismo tiempo, uno por cada cara, las partes reflejada y transmitida interferirán y los fotones perderán sus identidades individuales. Detectaremos un fotón en ambos detectores el 25% de las veces, y será entonces imposible decir si ambos fotones se reflejaron o transmitieron. Sólo se mide la propiedad relativa: que han ido a detectores diferentes.
Un divisor de haces, o espejo semirreflector, refleja la mitad de la luz que incide en él y transmite la otra mitad. Cada fotón tiene una probabilidad de mitad y mitad de reflejarse o de transmitirse. Si dos fotones idénticos inciden en el divisor de haz al mismo tiempo, uno por cada cara, las partes reflejada y transmitida interferirán y los fotones perderán sus identidades individuales. Detectaremos un fotón en ambos detectores el 25% de las veces, y será entonces imposible decir si ambos fotones se reflejaron o transmitieron. Sólo se mide la propiedad relativa: que han ido a detectores diferentes.
![]() […] Supongamos que los dos fotones dan en lados opuestos del espejo, alineadas sus trayectorias de forma que el camino de un fotón reflejado coincida con el de uno transmitido al otro, y viceversa. Un detector espera al final de cada trayectoria. Por norma, los dos fotones se reflejarán independientemente y habrá una probabilidad del 50% de que acaben en detectores distintos. Pero si los fotones son indistinguibles y llegan al espejo en el mismo instante, habrá una interferencia: se anularán ciertas posibilidades y no se producirán, en tanto que otras se reforzarán y se producirán más a menudo. Cuando los fotones interfieren, sólo hay una probabilidad del 25% de que terminen en detectores distintos. Además, cuando acaban en detectores distintos, equivale a detectar uno de los 4 posibles estados de Bell de los dos fotones, ese en que Alicia, decíamos, tenía «suerte». El 75% restante del tiempo los dos fotones terminan en un mismo detector, lo que corresponde a los otros tres estados de Bell, si bien no se discrimina entre ellos.
[…] Supongamos que los dos fotones dan en lados opuestos del espejo, alineadas sus trayectorias de forma que el camino de un fotón reflejado coincida con el de uno transmitido al otro, y viceversa. Un detector espera al final de cada trayectoria. Por norma, los dos fotones se reflejarán independientemente y habrá una probabilidad del 50% de que acaben en detectores distintos. Pero si los fotones son indistinguibles y llegan al espejo en el mismo instante, habrá una interferencia: se anularán ciertas posibilidades y no se producirán, en tanto que otras se reforzarán y se producirán más a menudo. Cuando los fotones interfieren, sólo hay una probabilidad del 25% de que terminen en detectores distintos. Además, cuando acaban en detectores distintos, equivale a detectar uno de los 4 posibles estados de Bell de los dos fotones, ese en que Alicia, decíamos, tenía «suerte». El 75% restante del tiempo los dos fotones terminan en un mismo detector, lo que corresponde a los otros tres estados de Bell, si bien no se discrimina entre ellos.
Cuando Alicia detecta simultáneamente un fotón en cada detector, el fotón B de Benito se convierte al instante en una copia del fotón original de Alicia, el X, que a su vez cambia irremediablemente de estado.
![]() En efecto: el estado inicial de las tres partículas es la siguiente superposición cuántica:
En efecto: el estado inicial de las tres partículas es la siguiente superposición cuántica:
![]() Así que, tras la operación de medida que hace Alicia, lanzando los fotones A y X sobre el dispositivo consistente en un divisor de haz con sendos detectores tras los dos canales de salida, hay cuatro posibles resultados de la experiencia, los 4 estados de Bell:
Así que, tras la operación de medida que hace Alicia, lanzando los fotones A y X sobre el dispositivo consistente en un divisor de haz con sendos detectores tras los dos canales de salida, hay cuatro posibles resultados de la experiencia, los 4 estados de Bell:
![]() Alicia va a determinar si los dos fotones A y X por la medida («medición de estados de Bell») pasan o no a estar en el estado de Bell
Alicia va a determinar si los dos fotones A y X por la medida («medición de estados de Bell») pasan o no a estar en el estado de Bell , es decir, si tras su operación, el resultado es ese estado precisamente (25% de las veces), o bien uno de los otros tres restantes posibles (75% de las veces, sin posibilidad de distinción con este primer montaje); los 4 son mutuamente ortogonales entre sí:
-El 25% de las veces hay detección conjunta: corresponde al caso en que los fotones A y X han quedado en el estado de Bell , que es el único de los 4 con simetría fermiónica. Y éste es el caso de éxito: en que Benito ya tiene un fotón copia del X:
-La explicación matemática radica en la actuación del divisor de haz cuando los dos fotones incidentes están en el estado de Bell con simetría fermiónica, , caso en el que se produce un efecto de antiagrupamiento, «antibunching», resultando en que el estado permanece inalterado:
.
![]() En la medida de Bell que se hace en el experimento de teletransporte de Innsbruck, la teleportación se conoce como efectivamente realizada en el 25% de los casos en que se produce detección en coincidencia, esto es, los respectivos detectores de los canales r y t señalan detección fotónica simultánea.
En la medida de Bell que se hace en el experimento de teletransporte de Innsbruck, la teleportación se conoce como efectivamente realizada en el 25% de los casos en que se produce detección en coincidencia, esto es, los respectivos detectores de los canales r y t señalan detección fotónica simultánea.
![]() Son las interferencias cuánticas (se trata de partículas indistinguibles) las que hacen que la probabilidad de detección conjunta, es decir, que den señales en coincidencia los dos detectores, sea del 25%: el porcentaje de «tiradas» experimentales en que se alcanza de primeras la teleportación, correspondiente al porcentaje en que los fotones A y X resultan en el estado de Bell
Son las interferencias cuánticas (se trata de partículas indistinguibles) las que hacen que la probabilidad de detección conjunta, es decir, que den señales en coincidencia los dos detectores, sea del 25%: el porcentaje de «tiradas» experimentales en que se alcanza de primeras la teleportación, correspondiente al porcentaje en que los fotones A y X resultan en el estado de Bell .
-El caso es que, después de la medida de Bell que hace Alicia en L1, el fotón B (que está en L2) está correlacionado con el par (A,X) (ambos en L1) por lo que, por la medición de Bell que ha hecho Alicia en L1 sobre los fotones X y A, el fotón B de Benito en L2 ha de haber pasado a una de las cuatro posibilidades expresadas en los cuatro sumandos anteriores.
-el segundo factor en el primer sumando (en color naranja), salvo fase, es justamente el estado original inicial del fotón X, y va acompañado, en la combinación lineal, del estado de Bell del par (X,A) que corresponde precisamente a cuando los dos detectores señalan en coincidencia en el divisor de haz.
-B está correlacionado con los estados de Bell del par X,A: es decir, al determinar, midiendo sobre el par (X,A), cuál estado de Bell se obtiene, se sabe en qué estado se halla B. Existe, pues, una correlación perfecta entre ambas partes del sistema, que están así entrelazadas o enredadas.
![]() Con esa medida que realiza Alicia, por tanto, el fotón B de Benito queda:
Con esa medida que realiza Alicia, por tanto, el fotón B de Benito queda:
– bien en el estado original del X (en ese 25% de detección por los dos detectores),
– bien en ese estado mismo estado girado respecto a uno de los tres ejes (las restantes 75%, en que sólo un detector señala). En ese 75%, B sólo necesitaría girar la polarización de su fotón para tener la copia duplicada. El problema es que el montaje experimental ha de proporcionar información que permita distinguir hacia cuál de los tres sumandos se ha desplomado la superposición cuántica.
-¿Cómo habría de sabe qué ha de hacer, en su caso? Esperando que, por un canal clásico, Alicia le informe de cuál fue, de las 4 posibilidades, el resultado de Bell que obtuvo.
-Pero, de hecho, es complicado para Alicia determinar cuál estado concreto de Bell ha obtenido, a cuál sumando específico se ha desplomado la superposición inicial, salvo en el 25% en que hay detección conjunta, por los dos detectores. Hay que hacer más complejo el experimento para superar esta dificultad y aumentar la ratio de éxito en el teletransporte.
![]() La predicción teórica cuántica, para un esquema experimental más refinado, como el de la siguiente figura, que añade dos prismas analizadores de polarización, permite incrementar el porcentaje de éxito y alcanzar el 50% (cf. S.L. Braunstein and A. Mann, Phys. Rev. A51 (1995) R1727; cit. en H. Paul, Introduction to Quantum Optics, Cambridge Univ. Press, 2004, capítulo 13, p. 209):
La predicción teórica cuántica, para un esquema experimental más refinado, como el de la siguiente figura, que añade dos prismas analizadores de polarización, permite incrementar el porcentaje de éxito y alcanzar el 50% (cf. S.L. Braunstein and A. Mann, Phys. Rev. A51 (1995) R1727; cit. en H. Paul, Introduction to Quantum Optics, Cambridge Univ. Press, 2004, capítulo 13, p. 209):
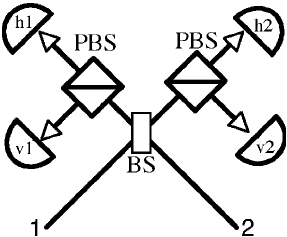
![]() A partir de las interferencias que se dan entre las distintas amplitudes cuánticas indistinguibles, se puede establecer que: la situación final colapsada se corresponde al 25% con cada uno de los sendos cuatro sumandos anteriores, estableciéndose una correspondencia entre las señales que proporcionan los detectores y el estado final. Esta correlación se produce de la siguiente forma:
A partir de las interferencias que se dan entre las distintas amplitudes cuánticas indistinguibles, se puede establecer que: la situación final colapsada se corresponde al 25% con cada uno de los sendos cuatro sumandos anteriores, estableciéndose una correspondencia entre las señales que proporcionan los detectores y el estado final. Esta correlación se produce de la siguiente forma:
–Caso : cuando los dos fotones son registrados por separado, en detectores distintos, bien en la pareja de detectores H1-V2, bien en la H2-V1 (el camino en retrodicción de cada fotón puede relatarse como a través de prismas distintos y las polarizaciones en que quedan finalmente son opuestas), significa que el estado final conjunto de los tres fotones es el
; ocurre un 25% de las veces. En este caso, el teletransporte se ha realizado instantáneamente.
–Caso : cuando los dos fotones son registrados de nuevo en sendos detectores distintos, pero ahora bien en la pareja de detectores H1-V1, bien en la H2-V2 (el camino en retrodicción de cada fotón puede relatarse como a través del mismo prisma y las polarizaciones en que quedan finalmente son opuestas), significa que el estado final conjunto de los tres fotones es el
; ocurre un 25% de las veces. En estos casos, todavía se puede lograr el éxito: cuando Alicia observa, a partir de los detectores que señalan, que con su medida de Bell ha logrado un estado final
, basta con añadir una operación adicional, a realizar por Blas sobre su fotón B, para culminar el teletransporte. Y ello porque, en este caso, Alicia sabe que el fotón de Blas ha resultado en el estado
,
que es un estado que puede ser reconvertido al original
,
haciendo atravesar el fotón B por una lámina de media onda con su eje orientado verticalmente. Blas lo puede hacer en cuanto, por el canal clásico, Alicia le informe de que están en ese caso; de esta forma, se logra el teletransporte –aunque con retraso- en este 25% adicional de los casos. ¡Y todo ello, sin que Alicia ni Blas sepan cuál es ese estado! (es decir, sin disponer de la información de cuáles son los valores de las constantes y
).
–Casos ,
: las restantes 50% de las veces, cuando los dos fotones son registrados en el mismo detector, que puede ser con igual probabilidad cualquiera de los cuatro, sólo se puede afirmar que el estado final es bien el
, bien el
: no hay manera de discriminar entre dos posibilidades. Éstos van a ser con este montaje los casos fallidos, ya que no se va a poder ultimar el teletransporte deseado.
![]() Ahora bien, en otro tipo de protocolos, como el del experimento en Roma por el equipo de De Martini, Alicia siempre se puede discriminar entre todos los estados finales, de forma que se dispone en todas las experiencias de la información requerida para que el teletransporte se ultime. En estos casos, se hablará de “teleportación determinista”, ya que en todos los eventos –en teoría- se culmina la teleportación, pero quizás el adjetivo no es muy adecuado, pues el azar sigue operando siempre en cuanto al resultado final concreto de las medidas de Alicia, impidiendo en todo caso la comunicación superlumínica.
Ahora bien, en otro tipo de protocolos, como el del experimento en Roma por el equipo de De Martini, Alicia siempre se puede discriminar entre todos los estados finales, de forma que se dispone en todas las experiencias de la información requerida para que el teletransporte se ultime. En estos casos, se hablará de “teleportación determinista”, ya que en todos los eventos –en teoría- se culmina la teleportación, pero quizás el adjetivo no es muy adecuado, pues el azar sigue operando siempre en cuanto al resultado final concreto de las medidas de Alicia, impidiendo en todo caso la comunicación superlumínica.
![]() De manera que, en el experimento de Innsbruck, si Alicia observa –esto es, los correspondientes detectores señalan- que con su medida de Bell ha logrado un estado final
De manera que, en el experimento de Innsbruck, si Alicia observa –esto es, los correspondientes detectores señalan- que con su medida de Bell ha logrado un estado final , al instante sabe que Blas ya tiene un fotón B en un estado réplica del que tenía originalmente el X (que ya ha cambiado, de manera que hay réplica pero no duplicado).
![]() Pero obsérvese que Blas no lo puede saber, porque se encuentra en el alejado lugar L2, y el resultado de la medida de Bell es azaroso y nadie puede predecir a priori cuando va a obtenerse ese teletransporte directo, que sólo ocurre en un porcentaje reducido de los casos (recordemos de nuevo: no hay manera de construir un teléfono cuántico que transmita información de forma instantánea). Aquí es donde se necesita que intervenga un canal clásico: Alicia ha de informar a Blas a través de él si ya tiene la réplica de su fotón o no.
Pero obsérvese que Blas no lo puede saber, porque se encuentra en el alejado lugar L2, y el resultado de la medida de Bell es azaroso y nadie puede predecir a priori cuando va a obtenerse ese teletransporte directo, que sólo ocurre en un porcentaje reducido de los casos (recordemos de nuevo: no hay manera de construir un teléfono cuántico que transmita información de forma instantánea). Aquí es donde se necesita que intervenga un canal clásico: Alicia ha de informar a Blas a través de él si ya tiene la réplica de su fotón o no.
![]() Es por esto por lo que muchos no aceptan que ni siquiera en las ocasiones en que Blas no debe hacer nada sobre su fotón, porque ya tiene sin más uno en el estado en que estaba el original que tenía Alicia, pueda hablarse de teleportación instantánea: no la ha habido si se toma la convención de que el teletransporte sólo se ha culminado cuando una información se ha transmitido “efectivamente”, y esto sólo sucede cuando el receptor ya la conoce: ha de esperar la información que viaja por el canal clásico.
Es por esto por lo que muchos no aceptan que ni siquiera en las ocasiones en que Blas no debe hacer nada sobre su fotón, porque ya tiene sin más uno en el estado en que estaba el original que tenía Alicia, pueda hablarse de teleportación instantánea: no la ha habido si se toma la convención de que el teletransporte sólo se ha culminado cuando una información se ha transmitido “efectivamente”, y esto sólo sucede cuando el receptor ya la conoce: ha de esperar la información que viaja por el canal clásico.
![]() Surge, quizás, una pregunta: ¿cómo estar seguros de que es cierto que se ha conseguido replicar el estado cuántico inicial del fotón X sobre el B?
Surge, quizás, una pregunta: ¿cómo estar seguros de que es cierto que se ha conseguido replicar el estado cuántico inicial del fotón X sobre el B?
![]() A. Acín, Investigación y Ciencia, septiembre 2006, p. 81:
A. Acín, Investigación y Ciencia, septiembre 2006, p. 81:
![]() Puesto que Bob tampoco puede determinar cuál es el estado cuántico de su sistema individual, puede parecer que se exige un acto de fe en la Mecánica Cuántica para aceptar que el estado de partida, desconocido, ha sido correctamente copiado en otro estado también desconocido. Pero todo esto puede comprobarse experimentalmente. Basta que un cuarto observador proporcione a Alice un gran número de sistemas individuales en el mismo estado puro
Puesto que Bob tampoco puede determinar cuál es el estado cuántico de su sistema individual, puede parecer que se exige un acto de fe en la Mecánica Cuántica para aceptar que el estado de partida, desconocido, ha sido correctamente copiado en otro estado también desconocido. Pero todo esto puede comprobarse experimentalmente. Basta que un cuarto observador proporcione a Alice un gran número de sistemas individuales en el mismo estado puro (es decir, idénticamente preparados de forma maximal). Alice reúne cada uno de ellos con la partícula A de una serie de pares auxiliares AB, efectúa una medición para ver cual es el estado de Bell que se obtiene en cada caso, e informa del resultado a Bob, que efectúa la correspondiente transformación sobre la partícula B del mismo par. Según la Mecánica Cuántica, el resultado en el punto L2 es una colección de sistemas individuales, todos ellos en el estado
, que debe ser igual al de partida. Disponiendo ahora de muchos sistemas individuales, es posible determinar sin ambigüedad cual es su estado cuántico, y comprobar si la predicción teórica es confirmada o no. Los experimentos citados al principio confirman que la respuesta es afirmativa.
![]() Finalmente, pueden estar seguros de que el fotón B está en el estado en que estaba X (aunque, al final, X ya no sigue en ese estado, ha cambiado, y ni Alicia ni Bob conocen el estado, en general).
Finalmente, pueden estar seguros de que el fotón B está en el estado en que estaba X (aunque, al final, X ya no sigue en ese estado, ha cambiado, y ni Alicia ni Bob conocen el estado, en general).
![]() En resumen, en cada teletransporte, hacia L2 sólo ha viajado:
En resumen, en cada teletransporte, hacia L2 sólo ha viajado:
-un fotón (el B), desde L3.
-información por un canal clásico, desde un sitio arbitrario. De hecho, Alicia puede contactar con Benito desde cualquier sitio; incluso, si desconoce dónde está, puede radiar el resultado de su medición sobre el par XA, de forma que Benito capte el mensaje: «la teleportacion no es un proceso direccional» (Cf. G. García Alcaine, Revista Española de Física, 12, nº 1, 6 (1998).
Transmisión de información cuántica, 1 qubit, por medio de un estado entrelazado y 2 bits clásicos.
![]() A. Acín, Investigación y Ciencia, septiembre 2006, p. 81:
A. Acín, Investigación y Ciencia, septiembre 2006, p. 81:
![]() Alguien pudiera inferir que la teleportación implica que un bit cuántico es equivalente a dos bits clásicos. Una deducción falsa. Si el emisor quisiera especificarle el bit cuántico al receptor por medio de información clásica, tendría que dar una dirección en la esfera de Poincaré. Para hacerlo con buena precisión, se requeriría un gran número de bits clásicos (infinitos para conseguir una imprecisión nula). Además, en la teleportación el emisor no tiene por qué conocer el bit cuántico que envía.
Alguien pudiera inferir que la teleportación implica que un bit cuántico es equivalente a dos bits clásicos. Una deducción falsa. Si el emisor quisiera especificarle el bit cuántico al receptor por medio de información clásica, tendría que dar una dirección en la esfera de Poincaré. Para hacerlo con buena precisión, se requeriría un gran número de bits clásicos (infinitos para conseguir una imprecisión nula). Además, en la teleportación el emisor no tiene por qué conocer el bit cuántico que envía.
![]() El entrelazamiento compartido por las dos partes es el recurso esencial en que se basa la teleportación. Esta se consume una vez el receptor ha reconstruido el bit cuántico: el entrelazamiento no sobrevive tras el final del proceso.
El entrelazamiento compartido por las dos partes es el recurso esencial en que se basa la teleportación. Esta se consume una vez el receptor ha reconstruido el bit cuántico: el entrelazamiento no sobrevive tras el final del proceso.
![]() Debemos retener lo siguiente: si emisor y receptor comparten un estado de dos qubits máximamente entrelazado, será posible el envío de un qubit sin errores por medio de la teleportación.
Debemos retener lo siguiente: si emisor y receptor comparten un estado de dos qubits máximamente entrelazado, será posible el envío de un qubit sin errores por medio de la teleportación.
![]() Una pregunta surge de modo natural: ¿de qué forma emisor y receptor consiguen establecer el entrelazamiento inicial requerido para la teleportación? El emisor puede, en principio, preparar el estado localmente y enviar al receptor uno de los dos bits cuánticos. Sin embargo, debe hacerlo a través del canal que poseen, que es ruidoso. Recordemos que se debe crear una superposición coherente de 00 y 11; los mecanismos generadores de decoherencia del canal repercutirán en el estado enviado; emisor y receptor acabarán compartiendo una versión ruidosa del estado deseado, que no permitirá una teleportación perfecta.
Una pregunta surge de modo natural: ¿de qué forma emisor y receptor consiguen establecer el entrelazamiento inicial requerido para la teleportación? El emisor puede, en principio, preparar el estado localmente y enviar al receptor uno de los dos bits cuánticos. Sin embargo, debe hacerlo a través del canal que poseen, que es ruidoso. Recordemos que se debe crear una superposición coherente de 00 y 11; los mecanismos generadores de decoherencia del canal repercutirán en el estado enviado; emisor y receptor acabarán compartiendo una versión ruidosa del estado deseado, que no permitirá una teleportación perfecta.
![]() En términos de información cuántica, con el diseño expuesto, con prismas incorporados, la eficiencia final teórica es pues del 50%, que son las veces que teóricamente se debería lograr teletransportar un qubit (el estado
En términos de información cuántica, con el diseño expuesto, con prismas incorporados, la eficiencia final teórica es pues del 50%, que son las veces que teóricamente se debería lograr teletransportar un qubit (el estado , con el uso imprescindible de dos qubits máximamente entrelazados (el estado de Bell) y dos bits clásicos (la información que Alicia debe mandar por el canal clásico para que Blas sepa en qué caso se está: un bit para comunicar si éxito o fracaso, y otro para que, en caso de éxito, Blas sepa si tiene que transformar su fotón o no). Por supuesto, la fidelidad teórica del 100% en ese 50% de las veces no se alcanzará, por las limitaciones y deficiencias prácticas usuales.
![]() Resumiendo: el teletransporte lo es de un estado cuántico, pero no hay transmisión de materia o radiación a distancia.
Resumiendo: el teletransporte lo es de un estado cuántico, pero no hay transmisión de materia o radiación a distancia.
–Tampoco hay violación de la Relatividad: no hay transmisión instantánea o a velocidad superlumínica de información.
-Se teletransporta el estado cuántico en general ignoto de un sistema, destruyendo el original.
-Se requiere una transmisión por un canal clásico para conocer si el experimento puede darse ya como concluido con éxito (25% de las veces); pendiente de alguna operación adicional para culminarlo (25% de las veces); o fracasado ese intento (50% de las veces), con porcentajes respectivamente referidos al montaje de Innsbruck sin y con prismas analizadores de polarización.
-El teletransporte se culmina sin que haya necesidad de que Alicia conozca ni el estado que se transfiere –es más, si no lo conoce, es imposible que lo pueda averiguar, a no ser que haya sido preparado por alguien y éste le pase la información- ni el lugar a donde se transfiere (allí donde está Blas).
![]() Detalles prácticos:
Detalles prácticos:
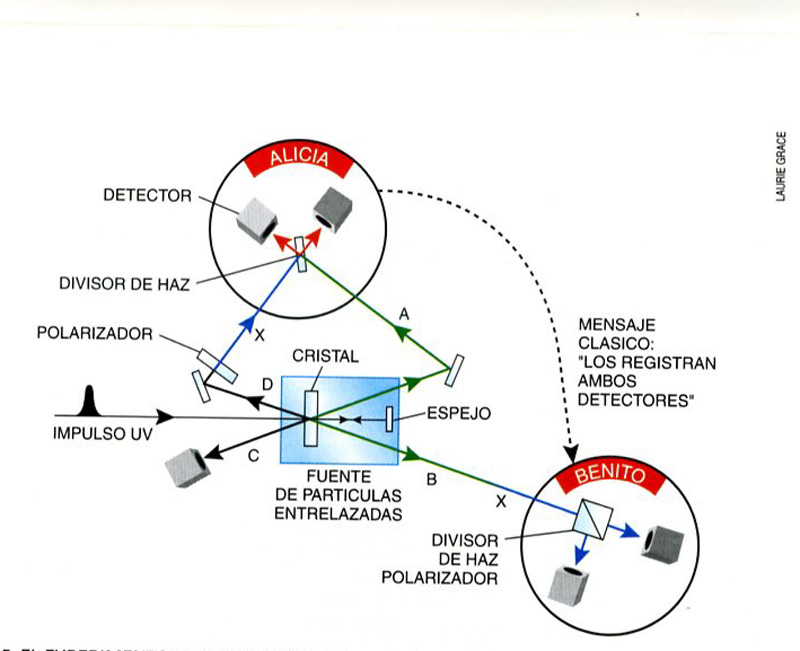
![]() Cf. Investigación y Ciencia, Temas 31, A. Zeilinger, Teletransporte cuántico, pp. 46-54:
Cf. Investigación y Ciencia, Temas 31, A. Zeilinger, Teletransporte cuántico, pp. 46-54:
-En la realización experimental anterior se comenta que se generaba un segundo par de fotones entrelazados, C y D; el segundo de éstos, D, era preparado en el estado X a teletransportar; para ello se le pasaba por un polarizador (momento a partir de cual deja de estar enredado con el C); cuando se detecte el fotón C, se sabe que Alicia ya dispone del X (antes D).
-Entonces se procede a la medida conjunta de A y X, combinándolos con un divisor de haz; cuando detecta un fotón en cada detector (25%), se lo notifica a Benito por un canal clásico.
-Benito, para comprobar que ha habido teletransporte, usa un polarizador y comprueba que el resultado es la polarización que en que se había preparado al X («si se le da a Alicia el fotón D=X sin polarizar, de manera que sigue entrelazado con el C, entonces, cuando el teletransporte tiene éxito, el fotón B de Benito acaba entrelazado con el C: se teletransmite de A a B el entrelazamiento con C»).
-Nota: luego aquí sí se conoce el estado de X (dice Zeilinger: «aunque nosotros lo sabemos, Alicia no lo sabe»). Alcaine solventa la cuestión recurriendo a las copias idénticamente preparadas:
![]() Alcaine, Teleportación: realidad y ficción, Rev. Españ. de Fís. 12, 1 (1998) 6:
Alcaine, Teleportación: realidad y ficción, Rev. Españ. de Fís. 12, 1 (1998) 6:
![]() Queda por comprobar que el estado teleportado coincide realmente con el de partida, cualquiera que sea éste. Para ello el experimento se repite muchas veces con fotones X de una misma polarización conocida, y se comprueba si los fotones B (en los casos en que el par (A,X) se encuentra en el estado
Queda por comprobar que el estado teleportado coincide realmente con el de partida, cualquiera que sea éste. Para ello el experimento se repite muchas veces con fotones X de una misma polarización conocida, y se comprueba si los fotones B (en los casos en que el par (A,X) se encuentra en el estado ) tienen dicha polarización, identificando y descontando las posibles fuentes de error. Tras repetir la tanda de experimentos con distintas polarizaciones iniciales (lineales y circulares), se concluye que, en todos los casos, el estado de polarización final del fotón B coincide con el estado de partida del fotón X, tal como predice la Mecánica Cuántica.
-Dice también Alcaine:
![]() Aunque en principio podría determinarse en cual de los cuatro estados de Bell se encuentra el par (A,X), en esta primera realización experimental se han seleccionado sólo los casos en que al efectuar una medición adecuada sobre el par (A,X), éste se encuentra en el estado
Aunque en principio podría determinarse en cual de los cuatro estados de Bell se encuentra el par (A,X), en esta primera realización experimental se han seleccionado sólo los casos en que al efectuar una medición adecuada sobre el par (A,X), éste se encuentra en el estado , que es el más fácil de medir experimentalmente. En estos casos el fotón B del par inicialmente enredado se encuentra ya en el mismo estado que el fotón X de partida: la teleportación del estado se consigue pues como máximo en una cuarta parte de los casos (de hecho, sólo en ciertos casos llegan ambos fotones X, A al detector dentro de un umbral temporal adecuado, con lo que el porcentaje de casos en los que la teleportación se consigue es inferior al 25% ideal).
Resultados:![]()
-El estado del fotón X ha sido transferido al fotón B de Benito.
-Ni Alicia ni Benito saben cuál estado es ese, en general.
-El principio de indeterminación impide determinar el estado cuántico de una partícula individual por completo, pero no teletransportarlo (sin duplicación, porque se destruye o altera el original).
-Se ha transportado 1 qubit de información.
-Se ha destruido el estado original (del fotón X).
-Se necesita un canal dual cuántico/clásico
-Es interesante notar que el canal cuántico permite transferir de manera sencilla una cantidad en principio infinita de información clásica, debido a que el estado a teleportar podría ser una superposición de estados con coeficientes transcendentes (que para ser definidos en sistema binario requieren una secuencia infinita de ceros y unos).
Importante:
–No hay transmisión de materia o energía a distancia.
–No hay transmisión instantánea de información (¡no v > c!).
-Se teletransporta el estado cuántico de un sistema, destruyendo el original.
![]() Respecto al pionero experimento de 1997 por el equipo de De Martini en Roma, el protocolo aplicado difiere del antes expuesto en que la medida conjunta que realiza Alicia no es la de Bell sobre dos fotones antes referida, sino que, a partir de una sugerencia de Sandu Popescu, involucra dos aspectos complementarios de un fotón: la polarización y el camino asociado por el usual relato que se construye a partir de una observación posterior (el camino recorrido “en retrodicción”, podríamos decir).
Respecto al pionero experimento de 1997 por el equipo de De Martini en Roma, el protocolo aplicado difiere del antes expuesto en que la medida conjunta que realiza Alicia no es la de Bell sobre dos fotones antes referida, sino que, a partir de una sugerencia de Sandu Popescu, involucra dos aspectos complementarios de un fotón: la polarización y el camino asociado por el usual relato que se construye a partir de una observación posterior (el camino recorrido “en retrodicción”, podríamos decir).
![]() Boschi, D., Branca,S., De Martini, F., Hardy, L. and Popescu, S., Experimental realization of teleporting an unknown pure quantum state via dual classical and Einstein-Podolsky-Rosen channels, Phys. Rev. Lett. 80 (1998) 1121-1125; también en arxiv.org y en semanticscholar.org:
Boschi, D., Branca,S., De Martini, F., Hardy, L. and Popescu, S., Experimental realization of teleporting an unknown pure quantum state via dual classical and Einstein-Podolsky-Rosen channels, Phys. Rev. Lett. 80 (1998) 1121-1125; también en arxiv.org y en semanticscholar.org:
![]() Abstract: We report on a quantum optical experimental implementation of teleportation of unknown pure quantum states. This realizes all the nonlocal aspects of the original scheme proposed by Bennett et al. and is equivalent to it up to a local operation. We exhibit results for the teleportation of a linearly polarised state and of an elliptically polarised state. We show that the experimental results cannot be explained in terms of a classical channel alone.
Abstract: We report on a quantum optical experimental implementation of teleportation of unknown pure quantum states. This realizes all the nonlocal aspects of the original scheme proposed by Bennett et al. and is equivalent to it up to a local operation. We exhibit results for the teleportation of a linearly polarised state and of an elliptically polarised state. We show that the experimental results cannot be explained in terms of a classical channel alone.
-La siguiente figura recoge el esquema básico del procedimiento, que sus autores afirmaban que, con las adecuadas implementaciones de dispositivos requeridos, llegaría a proporcionar una efectividad ideal del 100% -se trataría pues de una teleportación «determinista», según se explicó antes. La teleportación se culminó sobre unos pocos metros y, frente a los tres fotones que intervenían en el protocolo anterior de Innsbruck, sólo se involucran un par de fotones entrelazados en cada realización.
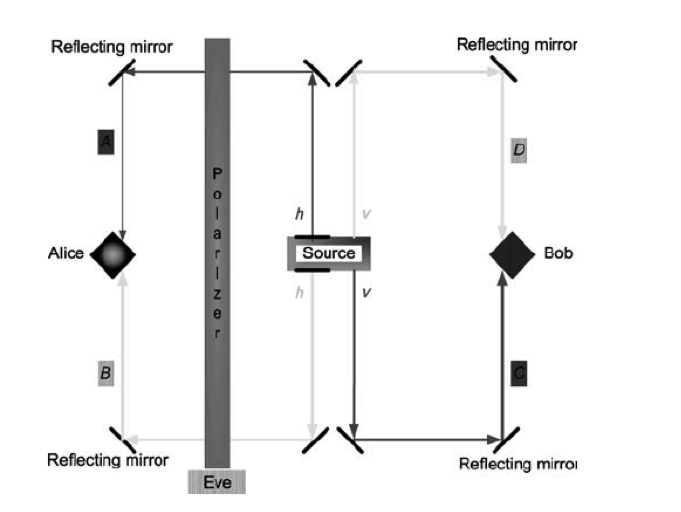
-Pares de fotones entrelazados en polarización son producidos a partir de un cristal nolineal (SPDC tipo II); los fotones de cada par se llevan a través de sendas calcitas, de forma que el entrelazamiento en polarizaciones se convierte en entrelazamiento en , esto es, en caminos fotónicos: la parte de la función de onda en
o caminos puede decirse que en este montaje «juega el papel del par EPR requerido para el teletransporte». Puesto que en cada camino de los dos posibles para cada fotón la polarización de este es la misma, el grado de libertad de polarización se convierte en un factor global de la parte de la función de onda entrelazada (parte en
) , «liberada» para constituir el soporte del estado a teletransportar. Para conseguirlo, se impone sobre el fotón horizontal 1–el que llegará a Alicia- el estado que se quiere teletransportar hacia el fotón 2 vertical, el que llegará a Blas. Para ello, se interpone un polarizador en su camino; en la realización usaron polarizadores bien lineales, bien elípticos (el caso general de polarización). Tras atravesarlo, ese fotón preparado ya en un estado ignoto,
, llega a Alicia –por el principio de indeterminación, no tiene manera de averiguarlo-, quien procede a realizar unas operaciones sobre él (medidas de varias combinaciones de polarizaciones y caminos), las cuales juegan el papel análogo a la medida de Bell que se realiza en el protocolo anterior de Innsbruck, pero ahora se realizan sobre un solo fotón y no sobre dos. Estas medidas, sin desplomar el entrelazamiento, le permiten a Alicia obtener una información que, enviada a Blas por un canal clásico, le permite a éste determinar las operaciones que ha de hacer a su vez sobre su fotón 2 para tener garantía de que («idealmente» para ciertos montajes en el 100% de los casos, ineficiencias prácticas y decoherencia aparte) su fotón acabará finalmente en el estado en que se había preparado el fotón 1 (y que Alicia no podía de ninguna manera averiguar). Como es obligado, en el momento en que el teletransporte se ha culminado, el fotón 1 de Alicia se ha alterado y ya no está en ese estado: no se ha producido su duplicación.
![]() F. De Martini and F. Sciarrino, Twenty Years of Quantum State Teleportation at the Sapienza University in Rome, Entropy 21 (2019) 768; doi:10.3390/e21080768.
F. De Martini and F. Sciarrino, Twenty Years of Quantum State Teleportation at the Sapienza University in Rome, Entropy 21 (2019) 768; doi:10.3390/e21080768.
![]() Sudbery, The fastest way from A to B, Nature 390 (1997) 551-552.
Sudbery, The fastest way from A to B, Nature 390 (1997) 551-552.
Algunos hitos en teletransporte fotónico
![]() Sucesivos hitos de teletransporte fotónico –sobre fotones, no de fotones- han sido, por ejemplo:
Sucesivos hitos de teletransporte fotónico –sobre fotones, no de fotones- han sido, por ejemplo:
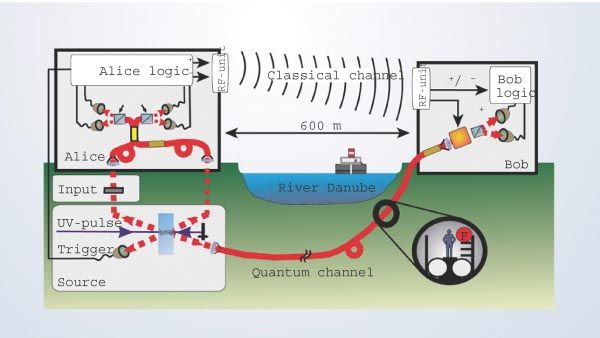
-en 2004, récord de 600 metros, realizándose un teletransporte bajo las aguas del Danubio, de orilla a orilla, mediante fibra óptica:
![]() Ursin, R. et al.; Quantum teleportation across the Danube; Nature 430 (2004) 849.
Ursin, R. et al.; Quantum teleportation across the Danube; Nature 430 (2004) 849.
-en 2010, teletransporte sobre una distancia de 16 kilómetros y transmisión al aire libre, algo que se considera un avance fundamental cara a establecer en el futuro una red cuántica de comunicaciones vía satélite, publicado en Nature Photonics;
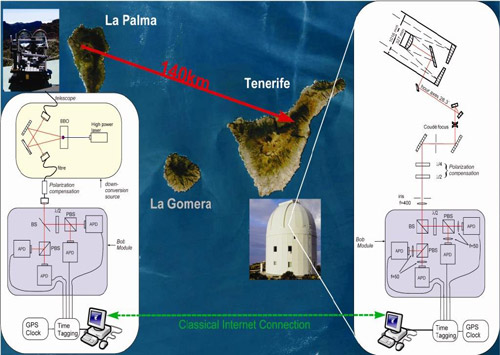
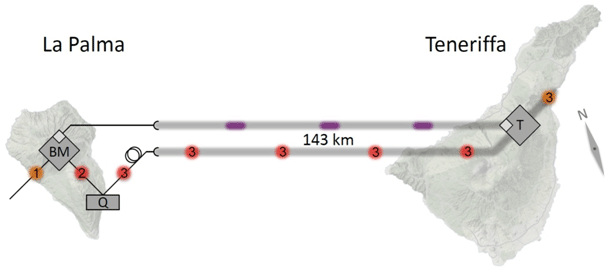
-en 2012, dos experimentos también con transmisión de fotones al aire libre, uno en Shanghái, unos 1100 fotones en cuatro horas y sobre 97 km, a través de un lago; el mismo año, teletransporte sin fibra entre las islas de La Palma y Tenerife, sobre 143 kilómetros –apartado siguiente-, financiado por la ESA (Agencia Espacial Europea);
-en 2015 y en Estados Unidos, equipo investigador de Takesue et al y publicación en la revista Optica, un teletransporte sobre 100 km, esta vez usando fibra óptica y con la novedad del uso de unos detectores de radiación monofotónica, hechos con nuevos materiales superconductores, que aumentaban drásticamente la eficiencia de detección en la banda de frecuencias requerida;
-en 2015, un teletransporte de un estado que codifica información correspondiente simultáneamente a dos propiedades de un fotón, espín (polarización) y momento angular orbital, en China, por los investigadores Chaoyang Lu and Jian-Wei Pan;
![]() Rui-bo Jin, Scientific Reports vol. 5, article number 9333, 2015, Highly efficient entanglement swapping and teleportation at telecom wavelength;
Rui-bo Jin, Scientific Reports vol. 5, article number 9333, 2015, Highly efficient entanglement swapping and teleportation at telecom wavelength;
https://www.nature.com/articles/srep09333.
![]() Nuevo récord (2015, 62 millas) en teletransporte: Science , Physics Org.
Nuevo récord (2015, 62 millas) en teletransporte: Science , Physics Org.
-En 2016, el equipo de Jian-Wei Pan ultimó un teletransporte usando la red urbana de fibra óptica de la ciudad china de Hefei, un avance decisivo hacia la realización futura de una red urbana, algo así como un internet cuántico;
-en una línea similar y casi simultáneamente, esta vez con la red de fibra de la ciudad de Calgary, Wolfgang Tittel et al han realizado un teletransporte usando fotones originales de 1,532 nm de longitud de onda, cuyo estado se transfería sobre fotones de 795 nm, a distancias de unos 8,2 km. Si en Calgary se empleó la red de fibra comercial estándar, en la que se interrumpió cualquier otra transmisión para el experimento, en Hefei hicieron uso de una red de fibra ideada ex profeso para su uso en información cuántica, diseñada por tanto para minimizar las interferencias de este tipo de señales.
![]() Primer teletransporte simultáneo de dos propiedades cuánticas: espín y momento angular orbital fotónicos (2015, Physics World).
Primer teletransporte simultáneo de dos propiedades cuánticas: espín y momento angular orbital fotónicos (2015, Physics World).
![]() En la mayoría de estos experimentos se consiguieron elevadas tasas de fidelidad o correcta reproducción de la información teletransportada y una eficiencia o ratio de éxito en el experimento cercana a la teórica.
En la mayoría de estos experimentos se consiguieron elevadas tasas de fidelidad o correcta reproducción de la información teletransportada y una eficiencia o ratio de éxito en el experimento cercana a la teórica.
2007, 2012: Teletransportando con fotones entre las Islas Canarias
![]() R. Ursin et al, Entanglement-based quantum communication over 144 km, Nature Physics 3 (2007) 481-486.
R. Ursin et al, Entanglement-based quantum communication over 144 km, Nature Physics 3 (2007) 481-486.
![]() Abstract: Quantum entanglement is the main resource to endow the field of quantum information processing with powers that exceed those of classical communication and computation. In view of applications such as quantum cryptography or quantum teleportation, extension of quantum-entanglement-based protocols to global distances is of considerable practical interest. Here we experimentally demonstrate entanglement-based quantum key distribution over 144 km. One photon is measured locally at the Canary Island of La Palma, whereas the other is sent over an optical free-space link to Tenerife, where the Optical Ground Station of the European Space Agency acts as the receiver. This exceeds previous free-space experiments by more than an order of magnitude in distance, and is an essential step towards future satellite-based quantum communication and experimental tests on quantum physics in space.
Abstract: Quantum entanglement is the main resource to endow the field of quantum information processing with powers that exceed those of classical communication and computation. In view of applications such as quantum cryptography or quantum teleportation, extension of quantum-entanglement-based protocols to global distances is of considerable practical interest. Here we experimentally demonstrate entanglement-based quantum key distribution over 144 km. One photon is measured locally at the Canary Island of La Palma, whereas the other is sent over an optical free-space link to Tenerife, where the Optical Ground Station of the European Space Agency acts as the receiver. This exceeds previous free-space experiments by more than an order of magnitude in distance, and is an essential step towards future satellite-based quantum communication and experimental tests on quantum physics in space.
![]() Xiao-song Ma et al, Quantum teleportation using active feed-forward between two Canary Islands , Nature 489 (2012) 269-273: http://www.nature.com/nature/journal/v489/n7415/abs/nature11472.html ; http://arxiv.org/pdf/1205.3909.pdf.
Xiao-song Ma et al, Quantum teleportation using active feed-forward between two Canary Islands , Nature 489 (2012) 269-273: http://www.nature.com/nature/journal/v489/n7415/abs/nature11472.html ; http://arxiv.org/pdf/1205.3909.pdf.
![]() Abstract: The quantum internet is predicted to be the next-generation information processing platform, promising secure communication and an exponential speed-up in distributed computation. The distribution of single qubits over large distances via quantum teleportation is a key ingredient for realizing such a global platform. By using quantum teleportation, unknown quantum states can be transferred over arbitrary distances to a party whose location is unknown. Since the first experimental demonstrations of quantum teleportation of independent external qubits, an internal qubit and squeezed states, researchers have progressively extended the communication distance. Usually this occurs without active feed-forward of the classical Bell-state measurement result, which is an essential ingredient in future applications such as communication between quantum computers. The benchmark for a global quantum internet is quantum teleportation of independent qubits over a free-space link whose attenuation corresponds to the path between a satellite and a ground station. Here we report such an experiment, using active feed-forward in real time. The experiment uses two free-space optical links, quantum and classical, over 143 kilometres between the two Canary Islands of La Palma and Tenerife. To achieve this, we combine advanced techniques involving a frequency-uncorrelated polarization-entangled photon pair source, ultra-low-noise single-photon detectors and entanglement-assisted clock synchronization. The average teleported state fidelity is well beyond the classical limit of two-thirds. Furthermore, we confirm the quality of the quantum teleportation procedure without feed-forward by complete quantum process tomography. Our experiment verifies the maturity and applicability of such technologies in real-world scenarios, in particular for future satellite-based quantum teleportation.
Abstract: The quantum internet is predicted to be the next-generation information processing platform, promising secure communication and an exponential speed-up in distributed computation. The distribution of single qubits over large distances via quantum teleportation is a key ingredient for realizing such a global platform. By using quantum teleportation, unknown quantum states can be transferred over arbitrary distances to a party whose location is unknown. Since the first experimental demonstrations of quantum teleportation of independent external qubits, an internal qubit and squeezed states, researchers have progressively extended the communication distance. Usually this occurs without active feed-forward of the classical Bell-state measurement result, which is an essential ingredient in future applications such as communication between quantum computers. The benchmark for a global quantum internet is quantum teleportation of independent qubits over a free-space link whose attenuation corresponds to the path between a satellite and a ground station. Here we report such an experiment, using active feed-forward in real time. The experiment uses two free-space optical links, quantum and classical, over 143 kilometres between the two Canary Islands of La Palma and Tenerife. To achieve this, we combine advanced techniques involving a frequency-uncorrelated polarization-entangled photon pair source, ultra-low-noise single-photon detectors and entanglement-assisted clock synchronization. The average teleported state fidelity is well beyond the classical limit of two-thirds. Furthermore, we confirm the quality of the quantum teleportation procedure without feed-forward by complete quantum process tomography. Our experiment verifies the maturity and applicability of such technologies in real-world scenarios, in particular for future satellite-based quantum teleportation.
![]() Max-Planck Institute for QuantumOptics: http://www.mpq.mpg.de/4860079/12_09_06?c=4571681
Max-Planck Institute for QuantumOptics: http://www.mpq.mpg.de/4860079/12_09_06?c=4571681

![]() La noticia en medios de comunicación y divulgación: ABC, El País y el blog de F.R. Villatoro, «La ciencia de la mula Francis«.
La noticia en medios de comunicación y divulgación: ABC, El País y el blog de F.R. Villatoro, «La ciencia de la mula Francis«.
![]() China se apunta al teletransporte en Las Canarias, noticia de 2017: ABC Canarias.
China se apunta al teletransporte en Las Canarias, noticia de 2017: ABC Canarias.
Teletransportando también con (sobre) átomos
![]() Hasta ahora, hemos hablado de fenómenos de teletransporte realizados con fotones. ¿Es posible experimentar de forma similar con partículas materiales, como los átomos? Porque hay que reconocer que, dada las peculiaridades de los entes fotónicos, esa luz tan diferente a la más vulgar materia, tal vez un fenómeno cuántico como el teletransporte podría despertar menos sorpresa protagonizado por ellos que si culminado sobre entes materiales. Pues bien, hoy en día también tenemos ya realizados numerosos fenómenos de teletransporte con átomos, en los que las entidades original y receptora de la información cuántica o estado teletransportado no tienen por qué ser de la misma especie nuclear. Sirvan de ejemplos, sin entrar en muchos detalles:
Hasta ahora, hemos hablado de fenómenos de teletransporte realizados con fotones. ¿Es posible experimentar de forma similar con partículas materiales, como los átomos? Porque hay que reconocer que, dada las peculiaridades de los entes fotónicos, esa luz tan diferente a la más vulgar materia, tal vez un fenómeno cuántico como el teletransporte podría despertar menos sorpresa protagonizado por ellos que si culminado sobre entes materiales. Pues bien, hoy en día también tenemos ya realizados numerosos fenómenos de teletransporte con átomos, en los que las entidades original y receptora de la información cuántica o estado teletransportado no tienen por qué ser de la misma especie nuclear. Sirvan de ejemplos, sin entrar en muchos detalles:
-1998: Nielsen et al implementaron en Los Alamos un teletransporte del estado cuántico de un núcleo de carbono, de un par de ellos entrelazado, hacia un núcleo de hidrógeno, con moléculas de tricloroetileno, a partir de un fenómeno de resonancia magnética nuclear (un teletransporte “interespecies” materiales).
-2004: un grupo de investigadores (Riebe et al) de Innsbruck publica en Nature un experimento de teletransporte de un estado cuántico entre un par de iones de calcio encerrados en una trampa de iones, o dispositivo en el que se capturan iones confinándolos en una región del espacio, usualmente mediante la utilización de una combinación adecuada de campos eléctricos y magnéticos. De forma análoga al procedimiento seguido para con fotones, se entrelazan un par de iones y se realiza una posterior medida de Bell conjunta de uno de ellos con un tercer ión auxiliar, de modo que, siempre con la concurrencia de un canal clásico, se teletransportó el estado del correspondiente miembro del par entrelazado sobre su compañero, situado a una distancia de unos pocos metros.
-Este mismo año, 2004, otro grupo de investigadores (Barret et al), en su mayoría del NIST (National Institute of Standards and Technology, Colorado), publicaron también en Nature un teletransporte de un qubit atómico, con iones de berilio. En ambos casos, las distancias involucradas eran micrométricas y el procedimiento es determinista, en el sentido de que, idealmente, se obtiene éxito en todos los eventos (mientras que, para un protocolo probabilístico como el teletransporte fotónico al modo Bennett-Innsbruck, hay tan sólo, también teóricamente y no sólo en la práctica, un porcentaje estadístico de eventos en que se culmina con éxito).
-2009: Olmschenk et al publicaron en Science un experimento sobre una distancia de un metro, realizado en el JQI (Joint Quantum Institute, Universidad de Maryland, Michigan), en el que un qubit almacenado sobre un ión de yterbio en una trampa era teletransportado sobre otro segundo átomo, cuya trampa se situaba a 1 metro de la del primer átomo. Este logro, afirmaba Christopher Monroe, uno de sus autores, “encierra un gran potencial para establecer la base de un esquema de ‘repetidor cuántico’, que permita construir una red de memorias cuánticas extendiéndose sobre grandes distancias”.
-2012: Xiao-Hui Bao et al, en Hefei, China, teletransporte entre dos objetos macroscópicos, desde un conjunto de átomos de rubidio hasta otro similar, sobre una distancia de 150 metros, usando fotones entrelazados auxiliares.
-2013: Nölleke et al, teletransporte entre dos átomos atrapados en sendas trampas en laboratorios distantes entre sí 21 metros; se genera un entrelazamiento entre uno de los átomos y un fotón auxiliar y se usa otro fotón auxiliar para representar el qubit a teletransportar desde el otro átomo; la medida de Bell se realiza sobre los dos fotones involucrados.
-2013: Krauter et al, teletransporte de una secuencia de estados de espín atómicos entre dos objetos materiales distantes entre sí.
-Algunas referencias:
![]() M. Riebe et al, Deterministic quantum teleportation with atoms, Nature 429 (2004) 734-737.
M. Riebe et al, Deterministic quantum teleportation with atoms, Nature 429 (2004) 734-737.
![]() M. D. Barret et al, Deterministic quantum teleportation of atomic qubits, Nature 429 (2004) 737.
M. D. Barret et al, Deterministic quantum teleportation of atomic qubits, Nature 429 (2004) 737.
![]() S. Olmschenk, dissertation et al, Quantum Teleportation between Distant Matter Qubits, Science 323, 486 (2009).
S. Olmschenk, dissertation et al, Quantum Teleportation between Distant Matter Qubits, Science 323, 486 (2009).
![]() Abstract: Quantum teleportation is the faithful transfer of quantum states between systems, relying on the prior establishment of entanglement and using only classical communication during the transmission. We report teleportation of quantum information between atomic quantum memories separated by about 1 meter. A quantum bit stored in a single trapped ytterbium ion (Yb+) is teleported to a second Yb+ atom with an average fidelity of 90% over a replete set of states. The teleportation protocol is based on the heralded entanglement of the atoms through interference and detection of photons emitted from each atom and guided through optical fibers. This scheme may be used for scalable quantum computation and quantum communication.
Abstract: Quantum teleportation is the faithful transfer of quantum states between systems, relying on the prior establishment of entanglement and using only classical communication during the transmission. We report teleportation of quantum information between atomic quantum memories separated by about 1 meter. A quantum bit stored in a single trapped ytterbium ion (Yb+) is teleported to a second Yb+ atom with an average fidelity of 90% over a replete set of states. The teleportation protocol is based on the heralded entanglement of the atoms through interference and detection of photons emitted from each atom and guided through optical fibers. This scheme may be used for scalable quantum computation and quantum communication.
Y teletransportando también entre luz y materia
-En 2006: un equipo dirigido por Eugene Polzik realiza, en el Instituto Niels Bohr de Copenhague, realizó el primer teletransporte interespecies entre luz y materia. Siguiendo una propuesta experimental del español Ignacio Cirac y de Klemens Hammerer, se transfirió el estado de un pulso de radiación integrado por unos pocos fotones sobre un conjunto de 1012 átomos de cesio, haciendo uso de un entrelazamiento creado entre el conjunto de átomos y otro pulso auxiliar de radiación, que será sometido a medida conjunta por Alicia con el que se va a teletransportar. En concreto, las variables con las que concierne el estado teleportado son amplitud y fase, que se transfieren a un estado de oscilación del sistema de los 1012 átomos. Publicado en Nature, exhibieron datos que conferían al experimento una fidelidad del 60%.
![]() En 2014, Gisin et al, en Génova, teletransportaron de un estado fotónico sobre un ión (o sea, interespecie, desde la luz hacia la materia) en un cristal o dispositivo de memoria cuántica sólida a 25 km de distancia, con fibra óptica:
En 2014, Gisin et al, en Génova, teletransportaron de un estado fotónico sobre un ión (o sea, interespecie, desde la luz hacia la materia) en un cristal o dispositivo de memoria cuántica sólida a 25 km de distancia, con fibra óptica:
![]() N. Gisin et al, Quantum teleportation from a telecom-wavelength photon to a solid-state quantum, ArXiv 1401.5968v1:
N. Gisin et al, Quantum teleportation from a telecom-wavelength photon to a solid-state quantum, ArXiv 1401.5968v1:
![]() In quantum teleportation, the state of a single quantum system is disembodied into classical information and purely quantum correlations, to be later reconstructed onto a second system that has never directly interacted with the first one. This counterintuitive phenomenon is a cornerstone of quantum information science due to its essential role in several important tasks such as the long-distance transmission of quantum information using quantum repeaters. In this context, a challenge of paramount importance is the distribution of entanglement between remote nodes, and to use this entanglement as a resource for long-distance light-to-matter quantum teleportation. Here we demonstrate quantum teleportation of the polarization state of a telecom-wavelength photon onto the state of a solid-state quantum memory. Entanglement is established between a rare-earth-ion doped crystal storing a single photon that is polarization-entangled with a flying telecom-wavelength photon. The latter is jointly measured with another flying qubit carrying the polarization state to be teleported, which heralds the teleportation. The fidelity of the polarization state of the photon retrieved from the memory is shown to be greater than the maximum fidelity achievable without entanglement, even when the combined distances travelled by the two flying qubits is 25 km of standard optical fibre. This light-to-matter teleportation channel paves the way towards long distance implementations of quantum networks with solid-state quantum memories.
In quantum teleportation, the state of a single quantum system is disembodied into classical information and purely quantum correlations, to be later reconstructed onto a second system that has never directly interacted with the first one. This counterintuitive phenomenon is a cornerstone of quantum information science due to its essential role in several important tasks such as the long-distance transmission of quantum information using quantum repeaters. In this context, a challenge of paramount importance is the distribution of entanglement between remote nodes, and to use this entanglement as a resource for long-distance light-to-matter quantum teleportation. Here we demonstrate quantum teleportation of the polarization state of a telecom-wavelength photon onto the state of a solid-state quantum memory. Entanglement is established between a rare-earth-ion doped crystal storing a single photon that is polarization-entangled with a flying telecom-wavelength photon. The latter is jointly measured with another flying qubit carrying the polarization state to be teleported, which heralds the teleportation. The fidelity of the polarization state of the photon retrieved from the memory is shown to be greater than the maximum fidelity achievable without entanglement, even when the combined distances travelled by the two flying qubits is 25 km of standard optical fibre. This light-to-matter teleportation channel paves the way towards long distance implementations of quantum networks with solid-state quantum memories.
Panorama
![]() Avances: Review article: Advances in quantum teleportation (revisión a 2015): S. Pirandola et al, Nature Photonics 9 (2015) 641-652
Avances: Review article: Advances in quantum teleportation (revisión a 2015): S. Pirandola et al, Nature Photonics 9 (2015) 641-652
![]() En resumen: los avances realizados en el campo del teletransporte cuántico son imparables y se suceden continuamente, abarcando fotones y partículas materiales; variables discretas (polarizaciones fotónicas, niveles de energía atómicos, etc.) y continuas (Braunstein y Kimble, 1998, teletransporte de la función de onda de un modo de vibración del campo electromagnético); procedimientos probabilísticos (la información es sobre variables discretas, se codifica sobre fotones individuales y hay una estadística teórica fijada de antemano por el formalismo para éxito y fracaso) o deterministas (la información a teletransportar es sobre variables continuas y va codificada sobre muchos fotones, de forma que, aunque se pierdan algunos, y con ellos se reduzca la fidelidad, siempre puede reconstruirse la información enviada).
En resumen: los avances realizados en el campo del teletransporte cuántico son imparables y se suceden continuamente, abarcando fotones y partículas materiales; variables discretas (polarizaciones fotónicas, niveles de energía atómicos, etc.) y continuas (Braunstein y Kimble, 1998, teletransporte de la función de onda de un modo de vibración del campo electromagnético); procedimientos probabilísticos (la información es sobre variables discretas, se codifica sobre fotones individuales y hay una estadística teórica fijada de antemano por el formalismo para éxito y fracaso) o deterministas (la información a teletransportar es sobre variables continuas y va codificada sobre muchos fotones, de forma que, aunque se pierdan algunos, y con ellos se reduzca la fidelidad, siempre puede reconstruirse la información enviada).
-Junto a todos estos logros relatados, se está produciendo un desarrollo paralelo de las técnicas de corrección de errores en las transmisiones cuánticas, para lo que se requieren nuevos procedimientos no clásicos, ya que, por ejemplo, la redundancia, el enviar repetidos pulsos con la misma información, no es posible, al estar proscritas las duplicaciones de los estados cuánticos. A estas alturas nadie se sorprenderá si decimos que casi todas esas técnicas recurren al entrelazamiento cuántico, recurriendo a codificar cada bit cuántico en estados entrelazados de varios qubits, más robustos frente a la decoherencia que un solo qubit. Estos estados se transmiten y luego se procede a su decodificación; en ellos se ha codificado información adicional a la que se quiere transmitir, que puede utilizarse para identificar y corregir posibles errores producidos en el proceso.
-Ejemplos de estos procedimientos, que configuran por sí solos una nueva disciplina en la teoría de la información cuántica, la QEC (Quantum Error Correction), son los pioneros protocolos de corrección de errores propuestos en 1996 por Peter Shor y Richard Calderbank, de un lado, y Andrew Steane, de otro, que hacían uso de estados de 9 y 7 qubits, respectivamente. La QEC incluye tanto técnicas pasivas –corrección de errores producidos- como activas –prevención y supresión de errores; como meta primordial, se pretende conseguir implementar canales cuánticos de comunicación tolerantes a cierta tasa de errores, los inevitables ruidos omnipresentes en toda transmisión y en todo dispositivo como, por ejemplo, un computador cuántico. También se incorporan técnicas de destilación de entrelazamiento, que eliminan el ruido o alteraciones que puedan producirse en el par entrelazado, algo usual y que hay que controlar en un proceso de teletransporte.
![]() K. S. Chou et al; «Deterministic teleportation of a quantum gate between two logical qubits«, Nature 561 (2018) 368.
K. S. Chou et al; «Deterministic teleportation of a quantum gate between two logical qubits«, Nature 561 (2018) 368.
![]() Teleportación de estados multidimensionales: Yi-Han Luo et al, Phys. Rev. Lett. 123 (2019)070505:
Teleportación de estados multidimensionales: Yi-Han Luo et al, Phys. Rev. Lett. 123 (2019)070505:
![]() Abstract: Quantum teleportation allows a “disembodied” transmission of unknown quantum states between distant quantum systems. Yet, all teleportation experiments to date were limited to a two-dimensional subspace of quantized multiple levels of the quantum systems. Here, we propose a scheme for teleportation of arbitrarily high-dimensional photonic quantum states and demonstrate an example of teleporting a qutrit. Measurements over a complete set of 12 qutrit states in mutually unbiased bases yield a teleportation fidelity of 0.75(1), which is well above both the optimal single-copy qutrit state-estimation limit of 1/2 and maximal qubit-qutrit overlap of 2/3, thus confirming a genuine and nonclassical three-dimensional teleportation. Our work will enable advanced quantum technologies in high dimensions, since teleportation plays a central role in quantum repeaters and quantum networks.
Abstract: Quantum teleportation allows a “disembodied” transmission of unknown quantum states between distant quantum systems. Yet, all teleportation experiments to date were limited to a two-dimensional subspace of quantized multiple levels of the quantum systems. Here, we propose a scheme for teleportation of arbitrarily high-dimensional photonic quantum states and demonstrate an example of teleporting a qutrit. Measurements over a complete set of 12 qutrit states in mutually unbiased bases yield a teleportation fidelity of 0.75(1), which is well above both the optimal single-copy qutrit state-estimation limit of 1/2 and maximal qubit-qutrit overlap of 2/3, thus confirming a genuine and nonclassical three-dimensional teleportation. Our work will enable advanced quantum technologies in high dimensions, since teleportation plays a central role in quantum repeaters and quantum networks.
-Nota: un qutrit es una superposición cuántica de 3 estados.
![]() En la prensa: Europapress, agosto, 2019.
En la prensa: Europapress, agosto, 2019.
![]() Las principales aplicaciones en las que sin duda el fenómeno del teletransporte va a intervenir en el futuro son el desarrollo de redes cuánticas para la distribución de información y, como no, la construcción de los anhelados computadores cuánticos. Hemos dicho que la información se almacena en qubits, pero el problema de los estados entrelazados entre sistemas cuánticos es que son muy inestables, muy fácilmente desplomables a la menor interacción, y es muy difícil prevenir la acción del entorno sobre los sistemas cuánticos, la llamada decoherencia, cuando se pretende que esa información viaje largas distancias o permanezca almacenada tiempos largos. Con el teletransporte, se abre una nueva vía para contrarrestar este problema y hacer posible el intercambio de qubits entre lugares lejanos: los qubits se pueden transferir a distancia sin que tengan que viajar recorriendo el camino intermedio.
Las principales aplicaciones en las que sin duda el fenómeno del teletransporte va a intervenir en el futuro son el desarrollo de redes cuánticas para la distribución de información y, como no, la construcción de los anhelados computadores cuánticos. Hemos dicho que la información se almacena en qubits, pero el problema de los estados entrelazados entre sistemas cuánticos es que son muy inestables, muy fácilmente desplomables a la menor interacción, y es muy difícil prevenir la acción del entorno sobre los sistemas cuánticos, la llamada decoherencia, cuando se pretende que esa información viaje largas distancias o permanezca almacenada tiempos largos. Con el teletransporte, se abre una nueva vía para contrarrestar este problema y hacer posible el intercambio de qubits entre lugares lejanos: los qubits se pueden transferir a distancia sin que tengan que viajar recorriendo el camino intermedio.
![]() De modo que el teletransporte cuántico se ha configurado como una herramienta muy útil, en definitiva, para el futuro tanto de la computación cuántica como para el desarrollo de redes cuánticas de comunicación, abiertas o con seguridad e indescifrabilidad basadas en protocolos cuánticos (la criptografía cuántica, con procesos de distribución segura de claves ya desarrollados e incluso comercializados). De la importancia que se le da a esta nueva tecnología pueden dar una idea dos datos: uno, el que la agencia espacial china, el NSSC (Centro Nacional de Ciencia del Espacio, National Science Space Center), está desarrollando un programa de investigación, el QUESS (Quantum Experiments at Space Scale), en cuyo marco se proponen, entre otros fines, “estudiar el teletransporte a escala espacial”, para lo que parece van a lanzar próximamente (según afirmaban en su página en internet, en verano de 2016) un satélite. Y, segundo dato, el que la Unión Europea se proponga lanzar para 2018 un proyecto de mil millones de euros para investigación en las nuevas tecnologías cuánticas, es decir, al mismo nivel de financiación que ha dedicado a los proyectos de investigación sobre el grafeno y el cerebro.
De modo que el teletransporte cuántico se ha configurado como una herramienta muy útil, en definitiva, para el futuro tanto de la computación cuántica como para el desarrollo de redes cuánticas de comunicación, abiertas o con seguridad e indescifrabilidad basadas en protocolos cuánticos (la criptografía cuántica, con procesos de distribución segura de claves ya desarrollados e incluso comercializados). De la importancia que se le da a esta nueva tecnología pueden dar una idea dos datos: uno, el que la agencia espacial china, el NSSC (Centro Nacional de Ciencia del Espacio, National Science Space Center), está desarrollando un programa de investigación, el QUESS (Quantum Experiments at Space Scale), en cuyo marco se proponen, entre otros fines, “estudiar el teletransporte a escala espacial”, para lo que parece van a lanzar próximamente (según afirmaban en su página en internet, en verano de 2016) un satélite. Y, segundo dato, el que la Unión Europea se proponga lanzar para 2018 un proyecto de mil millones de euros para investigación en las nuevas tecnologías cuánticas, es decir, al mismo nivel de financiación que ha dedicado a los proyectos de investigación sobre el grafeno y el cerebro.
![]() Europa y la investigación estratégica en Tecnologías cuánticas.
Europa y la investigación estratégica en Tecnologías cuánticas.
![]() Sobre la teleportación cuántica vía satélite:
Sobre la teleportación cuántica vía satélite:
-Discusión en 2012 en Naukas, el blog de F. R. Villatoro: El teletransporte cuántico vía satélite
–2017: Lograda Teleportación Cuántica Tierra-Satélite; arxiv.org/abs/1707.00934: Ground-to-satellite quantum teleportation: Ren, JG., Xu, P., Yong, HL. et al. Ground-to-satellite quantum teleportation; Nature 549 (2017) 70-73; https://doi.org/10.1038/nature23675
-Al hilo: sobre la «nueva carrera espacial«… y como China, al parecer, puede estar ganándola.
-En abril de 2024, el satélite SpeQtral-1 sigue sin ser lanzado todavía.
Discusión filosófica
![]() Teletransportando… ¿una oveja?
Teletransportando… ¿una oveja?
-Si teletransportamos los estados cuánticos de todas los elementos (moléculas, átomos, electrones…) de una oveja, aunque destruimos la oveja original, tenemos otra ¿idéntica? (¿Dolly bis?).
![]() ¿Una identidad individual de un ser vivo contiene algo más?
¿Una identidad individual de un ser vivo contiene algo más?
(Nota: para teletransportar un objeto de unos pocos gramos habría que teletransportar en torno a bits de datos).
-en MC, partículas en el mismo estado cuántico son indistinguibles.
-un problema: se teletransportan estados cuánticos puros, que son unos estados muy frágiles…
![]() Hemos visto que el teletransporte lo es de información: reproducimos información condensada en qubits, trasladada desde un sistema hacia otro que ocupa un lugar que va consiguiéndose cada vez más distante; se replica el estado original del primero sobre el segundo (el estado cuántico, el sistema receptor de él puede ser de distinta naturaleza al original); el estado del sistema donante de estado queda alterado (no hay duplicación cuántica de estados) y se requiere el concurso de un canal clásico de transferencia de información (no hay transmisión instantánea de información: no hay conflicto con la relatividad).
Hemos visto que el teletransporte lo es de información: reproducimos información condensada en qubits, trasladada desde un sistema hacia otro que ocupa un lugar que va consiguiéndose cada vez más distante; se replica el estado original del primero sobre el segundo (el estado cuántico, el sistema receptor de él puede ser de distinta naturaleza al original); el estado del sistema donante de estado queda alterado (no hay duplicación cuántica de estados) y se requiere el concurso de un canal clásico de transferencia de información (no hay transmisión instantánea de información: no hay conflicto con la relatividad).
![]() Hay una quizás perturbadora pregunta que surge ante el fenómeno cuántico del teletransporte: ¿la identidad o “mismidad” de un sistema se la confieren la materia o luz que lo componen –sus átomos y fotones específicos integrantes- o sólo el estado cuántico que lo describe? Dicho en otras palabras, si lográramos en un lejano futuro teletransportar el estado cuántico global de todos, absolutamente todos, los elementos (moléculas, átomos, electrones, fotones, quarks…) que constituyen una oveja dada, digamos Dolly, proceso en que la dejaríamos completamente alterada (óbito probable), sobre un conjunto de elementos componentes idénticos situados en otro lugar distante, ¿el nuevo sistema sería Dolly? Desde luego luciría igual; y recordaría y sentiría igual, dicho sea con permiso de al menos algunos neurocientíficos -y de la evanescente alma, si es que algún animal, humano o no, la poseyera-, y asumiendo que, algo controvertido todavía para algunos, que el estado cuántico es la última y más completa descripción posible para un sistema.
Hay una quizás perturbadora pregunta que surge ante el fenómeno cuántico del teletransporte: ¿la identidad o “mismidad” de un sistema se la confieren la materia o luz que lo componen –sus átomos y fotones específicos integrantes- o sólo el estado cuántico que lo describe? Dicho en otras palabras, si lográramos en un lejano futuro teletransportar el estado cuántico global de todos, absolutamente todos, los elementos (moléculas, átomos, electrones, fotones, quarks…) que constituyen una oveja dada, digamos Dolly, proceso en que la dejaríamos completamente alterada (óbito probable), sobre un conjunto de elementos componentes idénticos situados en otro lugar distante, ¿el nuevo sistema sería Dolly? Desde luego luciría igual; y recordaría y sentiría igual, dicho sea con permiso de al menos algunos neurocientíficos -y de la evanescente alma, si es que algún animal, humano o no, la poseyera-, y asumiendo que, algo controvertido todavía para algunos, que el estado cuántico es la última y más completa descripción posible para un sistema.
![]() Además, hay algo muy inquietante, un peligro que acecha y que convirtió al protagonista del relato “La mosca”, de George Langelaan, en un monstruo: a la mínima intrusión de una interacción perturbadora en el proceso, ¿qué nuevo ser se habría fabricado? La decoherencia, simplemente, podría actuar como una diosa terrible, creadora o aniquiladora.
Además, hay algo muy inquietante, un peligro que acecha y que convirtió al protagonista del relato “La mosca”, de George Langelaan, en un monstruo: a la mínima intrusión de una interacción perturbadora en el proceso, ¿qué nuevo ser se habría fabricado? La decoherencia, simplemente, podría actuar como una diosa terrible, creadora o aniquiladora.
![]() George Langelaan, en su relato «La mosca»:
George Langelaan, en su relato «La mosca»:
![]() No, jamás olvidaré aquel cráneo aplastado, aquella cabeza de pesadilla, blanca, vellosa, con puntiagudas orejas de gato y ojos protegidos por grandes placas oscuras.
No, jamás olvidaré aquel cráneo aplastado, aquella cabeza de pesadilla, blanca, vellosa, con puntiagudas orejas de gato y ojos protegidos por grandes placas oscuras.
![]() Desde luego, no es que se atisbe semejante logro en el horizonte: para teletransportar un objeto de unos pocos gramos habría que teletransportar en torno a 1030 bits de datos; hay alrededor de 1029 partículas materiales en un cuerpo humano, con variados grados de libertad cada una (datos sacados de varias fuentes y cuya corrección no estoy en condiciones de probar)… ¿Qué medios se requerirían? ¿Cuánto tiempo llevaría? Aunque quizás bastaría teletransportar el cerebro, el mapa de conexiones neuronales… el resto podría duplicarse clásicamente. En todo caso, hoy por hoy (y por siglos… o billones de años) ni imaginable: implanteable y descartado por completo.
Desde luego, no es que se atisbe semejante logro en el horizonte: para teletransportar un objeto de unos pocos gramos habría que teletransportar en torno a 1030 bits de datos; hay alrededor de 1029 partículas materiales en un cuerpo humano, con variados grados de libertad cada una (datos sacados de varias fuentes y cuya corrección no estoy en condiciones de probar)… ¿Qué medios se requerirían? ¿Cuánto tiempo llevaría? Aunque quizás bastaría teletransportar el cerebro, el mapa de conexiones neuronales… el resto podría duplicarse clásicamente. En todo caso, hoy por hoy (y por siglos… o billones de años) ni imaginable: implanteable y descartado por completo.
![]() Pero, ¿se trata sólo de una limitación de medios? ¿No hay una limitación fundamental, de principios o leyes? ¿Tal vez sí de principios morales? Y si el donante no muere, sino que pervive convertido en otro ser, con su identidad irremediablemente alterada: ¿serían dos seres distintos, sin más conexión que haber estado en el mismo estado cuántico, en dos instantes diferentes de su existencia? Y ya puestos, en un teletransporte interespecies, ¿no podría teletransportarse un ser humano sobre un material menos fungible que la carne? ¿Quizás sobre un ordenador cuántico? ¿El ente destino podría ser considerado legalmente el reemplazo en sociedad del donante original? Transhumanismo, cyborgs…
Pero, ¿se trata sólo de una limitación de medios? ¿No hay una limitación fundamental, de principios o leyes? ¿Tal vez sí de principios morales? Y si el donante no muere, sino que pervive convertido en otro ser, con su identidad irremediablemente alterada: ¿serían dos seres distintos, sin más conexión que haber estado en el mismo estado cuántico, en dos instantes diferentes de su existencia? Y ya puestos, en un teletransporte interespecies, ¿no podría teletransportarse un ser humano sobre un material menos fungible que la carne? ¿Quizás sobre un ordenador cuántico? ¿El ente destino podría ser considerado legalmente el reemplazo en sociedad del donante original? Transhumanismo, cyborgs…
![]() Opinando: Star Trek, al lado de todo esto, era un juego de niños…
Opinando: Star Trek, al lado de todo esto, era un juego de niños…
Bibliografía
-Teleportación en IBM: http://researcher.watson.ibm.com/researcher/view_group.php?id=2862
-A.D. Aczel, Entrelazamiento, Crítica, Drakontos.
-G. Alcaine, Teleportación: realidad y ficción, Rev. Españ. de Fís. F 12, 1 (1998) 6-9.
-A. Acín, Investigación y Ciencia, septiembre 2006.
-H. Paul, Introduction to Quantum Optics, Cambridge Univ. Press, 2004, capítulo 13.
-A. Zeilinger, Teletransporte cuántico, Investigación y Ciencia, Temas 31, pp. 46-54.
-Presentación: http://qudev.ethz.ch/content/courses/QSIT10/presentations/QSIT-Teleportation.pdf
-G. Weihs and A. Zeilinger, Photon statistics at beam splitters: an essential tool in quantum information and teleportation.
-María C. Boscá, Computación, teleportación y criptografía cuánticas; Un paseo por el cosmos, RBA.
Dejar una contestacion